Giải mục 1 trang 46,47,48 SGK Toán 12 tập 1 - Kết nối tri thức

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 46 SGK Toán 12 Kết nối tri thức

Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ.

a) Các đoạn thẳng này cho biết gì về hướng và độ lớn của các các lực căng dây?

b) Các đoạn thẳng này có cùng nằm trong một mặt phẳng không?

Phương pháp giải:

Sử dụng kiến thức về biểu diễn lực qua đoạn thẳng có hướng: Dùng đoạn thẳng có hướng để biểu diễn lực căng dây. Hướng của đoạn thẳng chỉ hướng của của lực căng dây, độ dài đoạn thẳng thể hiện độ lớn của lực và được lấy tỉ lệ với độ lớn của lực.

Lời giải chi tiết:

a) Các đoạn thẳng này có hướng lên trên (về phía móc cần cẩu) và độ dài của các đoạn thẳng thể hiện cho độ lớn của các lực căng dây và được lấy tỉ lệ với độ lớn của các lực căng dây.

b) Các đoạn thẳng này không cùng nằm trên một mặt phẳng.

CH

Trả lời câu hỏi Câu hỏi trang 6 SGK Toán 12 Kết nối tri thức

Hình 2.3 cho ta ví dụ về một số đại lượng có thể biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự.

Phương pháp giải:

Sử dụng kiến thức về nhận biết vectơ trong không gian để tìm hình ảnh thực tế: Vectơ trong không gian là một đoạn thẳng có hướng.

Lời giải chi tiết:

Một số ví dụ khác:

a) Hướng bay của khinh khí cầu:

b) Hướng đi của thuyền trên sông:

LT1

Trả lời câu hỏi Luyện tập trang 47 SGK Toán 12 Kết nối tri thức

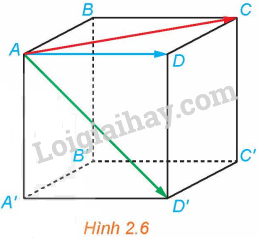
Cho hình lập phương ABCD.A’B’C’D’ (H.2.6). Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \):

a) Hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD)?

b) Hai vectơ nào có cùng độ dài?

Phương pháp giải:

+ Sử dụng kiến thức về giá của vectơ để tìm vectơ có giá nằm trong mặt phẳng (ABCD): Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ.

+ Sử dụng kiến thức về độ dài vectơ để tìm hai vectơ có cùng độ dài: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\)

Lời giải chi tiết:

a) Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \), hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} \) có giá nằm trong mặt phẳng (ABCD)

b) Vì ABCD.A’B’C’D’ là hình lập phương nên \(AD = DC = DD'\)

Tam giác ADD’ vuông tại D nên theo định lý Pythagore ta có:

\(AD' = \sqrt {A{D^2} + DD{'^2}}  = AD\sqrt 2 \)

Tam giác ADC vuông tại D nên theo định lý Pythagore ta có:

\(AC = \sqrt {A{D^2} + D{C^2}}  = AD\sqrt 2 \)

 Do đó, \(AD' = AC\) hay \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD'} } \right|\). Vậy hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD'} \) có cùng độ dài.

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 47 SGK Toán 12 Kết nối tri thức

Cho hình hộp ABCD.A’B’C’D’ (H.2.7)

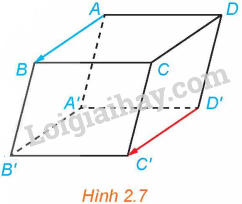
a) So sánh độ dài hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).

b) Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).

c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) có cùng phương không? Có cùng hướng không?

Phương pháp giải:

+ Sử dụng kiến thức về giá của vectơ: Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ.

+ Sử dụng kiến thức về độ dài vectơ: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).

Lời giải chi tiết:

a) Vì ABCD.A’B’C’D’ là hình hộp nên ABCD và DCC’D’ là các hình bình hành. Suy ra, \(AB = CD = D'C'\). Do đó, \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {D'C'} } \right|\).

b) Vì ABCD và DCC’D’ là các hình bình hành nên AB//CD, CD//C’D’. Do đó, AB//C’D’. Vậy giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) song song với nhau.

c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) cùng phương và cùng hướng.

CH

Trả lời câu hỏi Câu hỏi trang 47 SGK Toán 12 Kết nối tri thức

Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?

Phương pháp giải:

Sử dụng kiến thức về hai vectơ bằng nhau để giải bài toán: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a  = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.

Lời giải chi tiết:

Giả sử có ba vectơ \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \) sao cho: \(\overrightarrow a  = \overrightarrow b \) và \(\overrightarrow b  = \overrightarrow c \).

Vì \(\overrightarrow a  = \overrightarrow b \) nên hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\) (1)

Vì \(\overrightarrow b  = \overrightarrow c \) nên hai vectơ \(\overrightarrow c \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow c } \right| = \left| {\overrightarrow b } \right|\) (2)

Từ (1) và (2) ta có hai vectơ \(\overrightarrow a \), \(\overrightarrow c \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow c } \right|\). Do đó, \(\overrightarrow a  = \overrightarrow c \)

Do đó, hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó bằng nhau.

LT2

Trả lời câu hỏi Luyện tập 2 trang 48 SGK Toán 12 Kết nối tri thức

Cho hình chóp S. ABCD có đáy ABCD là hình bình hành.

a) Trong ba vectơ \(\overrightarrow {SC} ,\overrightarrow {AD} \) và \(\overrightarrow {DC} \), vectơ nào bằng vectơ \(\overrightarrow {AB} \).

b) Gọi M là một điểm thuộc cạnh AD. Xác định điểm N sao cho \(\overrightarrow {MN}  = \overrightarrow {AB} \).

Phương pháp giải:

Sử dụng kiến thức về hai vectơ bằng nhau để giải bài toán: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a  = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.

Lời giải chi tiết:

a) Vì ABCD là hình bình hành nên AB//CD và \(AB = CD\). Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) có cùng độ dài và cùng hướng nên hai vectơ đó bằng nhau.

Vì AB và SC chéo nhau nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) không cùng phương. Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) không bằng nhau.

Vì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không cùng phương nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không bằng nhau.

b) Qua M vẽ đường thẳng song song với AB cắt BC tại N.

Tứ giác ABNM có: AB//MN, AM//BN nên tứ giác ABNM là hình bình hành. Do đó, \(AB = MN\), lại có: AB//MN nên hai vectơ \(\overrightarrow {MN} ,\overrightarrow {AB} \) cùng độ dài và cùng hướng. Suy ra, \(\overrightarrow {MN}  = \overrightarrow {AB} \). Vậy điểm N cần tìm là giao điểm của đường thẳng qua M song song với AB và cạnh BC.

VD1

Trả lời câu hỏi Vận dụng 1 trang 48 SGK Toán 12 Kết nối tri thức

Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao.

Phương pháp giải:

Sử dụng kiến thức về hai vectơ bằng nhau để giải thích: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a  = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.

Lời giải chi tiết:

Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 15 lên tầng 22 của tòa nhà là \(\overrightarrow a \). Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 22 lên tầng 29 của tòa nhà là \(\overrightarrow b \).

Vì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều dịch chuyển từ tầng thấp lên tầng cao nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) có cùng hướng (1).

Độ dài vectơ \(\overrightarrow a \) là: \(\left| {\overrightarrow a } \right| = 7\), độ dài vectơ \(\overrightarrow b \) là: \(\left| {\overrightarrow b } \right| = 7\) nên \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 7\) (2)

Từ (1) và (2) ta có: \(\overrightarrow a  = \overrightarrow b \). Vậy các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau.