Lý thuyết tỉ lệ thức
Tỉ lệ thức là một đẳng thức của hai số
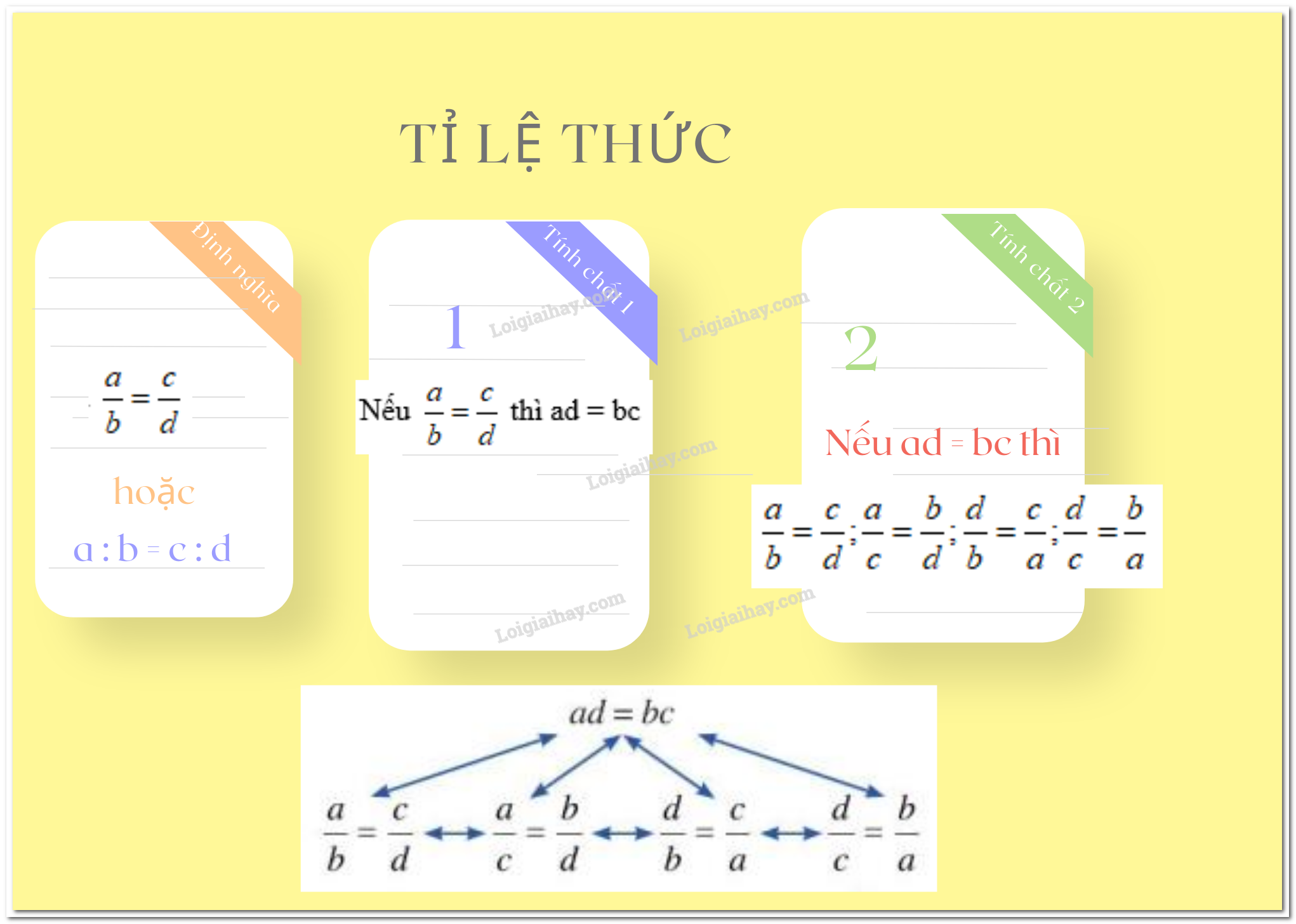
I. Các kiến thức cần nhớ
Định nghĩa tỉ lệ thức
+ Tỉ lệ thức là đẳng thức của hai tỉ số \(\dfrac{a}{b} = \dfrac{c}{d}\)
+ Tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\) còn được viết là \(a:b = c:d\)
Ví dụ: \(\dfrac{{28}}{{24}} = \dfrac{7}{6};\)\(\dfrac{3}{{10}} = \dfrac{{2,1}}{7}\)
Tính chất tỉ lệ thức
+ Tính chất 1 (tính chất cơ bản của tỉ lệ thức)
Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)
+ Tính chất 2 (điều kiện để bốn số lập thành tỉ lệ thức): Nếu \(ad=bc\) và \(a,b,c,d \ne 0\) thì ta có các tỉ lệ thức
\(\dfrac{a}{b} = \dfrac{c}{d}\); \(\dfrac{a}{c} = \dfrac{b}{d}\); \(\dfrac{d}{b} = \dfrac{c}{a};\) \(\dfrac{d}{c} = \dfrac{b}{a}.\)
Ví dụ: Ta có \(\dfrac{3}{6} = \dfrac{9}{{18}} \Rightarrow 3.18 = 9.6\left( { = 54} \right)\)
Vì \(4.9 = 3.12(=36)\) nên ta có các tỉ lệ thức sau: \(\dfrac{4}{3} = \dfrac{{12}}{9};\,\dfrac{3}{4} = \dfrac{9}{{12}};\dfrac{4}{{12}} = \dfrac{3}{9};\dfrac{{12}}{4} = \dfrac{9}{3}\)
II. Các dạng toán thường gặp
Dạng 1: Lập tỉ lệ thức từ đẳng thức cho trước
Phương pháp:
Ta sử dụng: Nếu \(a.d = b.c\) thì
\(\dfrac{a}{b} = \dfrac{c}{d}\); \(\dfrac{a}{c} = \dfrac{b}{d}\); \(\dfrac{d}{b} = \dfrac{c}{a};\) \(\dfrac{d}{c} = \dfrac{b}{a}.\)
Dạng 2: Tìm x, y
Phương pháp:
Sử dụng tính chất cơ bản của tỉ lệ thức: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)
Trong một tỉ lệ thức ta có thể tìm một số hạng chưa biết khi biết ba số hạng còn lại.
\(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow a = \dfrac{{bc}}{d};\,b = \dfrac{{ad}}{c};\)\(c = \dfrac{{ad}}{b};\,d = \dfrac{{bc}}{a}\) .
Ví dụ: Tìm x biết \(\dfrac{x}{2} = \dfrac{8}{6}\)
Ta có:
\(\begin{array}{l}
\dfrac{x}{2} = \dfrac{8}{6}\\
\Rightarrow x.6 = 8.2\\
\Rightarrow x = \dfrac{{16}}{6}\\
\Rightarrow x = \dfrac{8}{3}
\end{array}\)
Dạng 3: Chứng minh các tỉ lệ thức
Phương pháp:
Dựa vào các tính chất của tỉ lệ thức và biến đổi linh hoạt để chứng minh.
III. Bài tập vận dụng
Câu 1. Chọn câu đúng. Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì
A. \(a = c\)
B. \(a.c = b.d\)
C. \(a.d = b.c\)
D. \(b = d\)
Lời giải
Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)
Đáp án C
Câu 2. Chỉ ra đáp án sai: Từ tỉ lệ thức \(\dfrac{5}{9} = \dfrac{{35}}{{63}}\) ta có tỉ lệ thức sau:
A. \(\dfrac{5}{{35}} = \dfrac{9}{{63}}\)
B. \(\dfrac{{63}}{9} = \dfrac{{35}}{5}\)
C. \(\dfrac{{35}}{9} = \dfrac{{63}}{5}\)
D. \(\dfrac{{63}}{{35}} = \dfrac{9}{5}\)
Lời giải
Xét đáp án C: \(35.5 \ne 63.9\) do đó \(\dfrac{{35}}{9} \ne \dfrac{{63}}{5}\) nên C sai
Đáp án C
Câu 3. Các tỉ số nào sau đây lập thành một tỉ lệ thức?
A. \(\dfrac{7}{{12}}\) và \(\dfrac{5}{6}:\dfrac{4}{3}\)
B. \(\dfrac{6}{7}:\dfrac{{14}}{5}\) và \(\dfrac{7}{3}:\dfrac{2}{9}\)
C. \(\dfrac{{15}}{{21}}\) và \( - \dfrac{{125}}{{175}}\)
D. \(\dfrac{{ - 1}}{3}\) và \(\dfrac{{ - 19}}{{57}}\)
Lời giải
Ta có : \(\dfrac{5}{6}:\dfrac{4}{3} = \dfrac{5}{6}.\dfrac{3}{4} = \dfrac{5}{8} \ne \dfrac{7}{{12}}\) nên A sai.
\(\dfrac{6}{7}:\dfrac{{14}}{5} = \dfrac{6}{7}.\dfrac{5}{{14}} = \dfrac{{15}}{{49}}\) và \(\dfrac{7}{3}:\dfrac{2}{9} = \dfrac{7}{3}.\dfrac{9}{2} = \dfrac{{21}}{2} \ne \dfrac{{15}}{{49}}\) nên B sai.
\(\dfrac{{15}}{{21}} = \dfrac{5}{7} \ne - \dfrac{{125}}{{175}}\) nên C sai.
Ta có \(\dfrac{{ - 1}}{3} = \dfrac{{ - 19}}{{57}}\) vì \(\left( { - 1} \right).{\rm{ }}57 = 3.\left( { - 19} \right) = - 57\).
Do đó \(\dfrac{{ - 1}}{3}\) và \(\dfrac{{ - 19}}{{57}}\) lập thành tỉ lệ thức nên D đúng.
Đáp án D
Câu 4. Cho tỉ lệ thức \(\dfrac{x}{{15}} = \dfrac{{ - 4}}{5}\) thì:
A. \(x = \)\(\dfrac{{ - 4}}{3}\)
B. \(x = 4\)
C. \(x = - 12\)
D. \(x = - 10\)
Lời giải
\(\dfrac{x}{{15}} = \dfrac{{ - 4}}{5}\)
\(x.5 = 15.(-4)\)
\(5x = -60\)
\(x = -60 : 5\)
\(x = -12\)
Vậy x = -12.
Đáp án C
Câu 5. Có bao nhiêu giá trị \(x\) thỏa mãn \(\dfrac{{16}}{x} = \dfrac{x}{{25}}\)
A. \(1\)
B. \(2\)
C. \(0\)
D. \(3\)
Lời giải
\(\dfrac{{16}}{x} = \dfrac{x}{{25}}\)
x2 = 16 . 25
x2 = 400
\(x = 20\) hoặc \(x = - 20\)
Vậy \(x = 20\) hoặc \(x = - 20\).
Đáp án B
Câu 6. Biết cứ xay 100kg thóc thì được 60kg gạo. Hỏi muốn có 3 tạ gạo thì phải xay bao nhiêu tạ thóc?
A. 180 kg
B. 5 tạ
C. 2 tạ
D. 600 kg
Lời giải
Gọi khối lượng thóc cần để xay được 3 tạ = 300 kg gạo là x (kg) (x > 0 )
Vì tỉ lệ thóc : gạo xay được là không đổi nên ta có:
\(\dfrac{{100}}{{60}} = \dfrac{x}{{300}}\)
\(\begin{array}{l} 60x = 100.300\\ x = 500\end{array}\)
Vậy cần 500 kg = 5 tạ thóc để xay được 3 tạ gạo
Đáp án B
Câu 7. Giá trị nào của \(x\) thỏa mãn \(\dfrac{{ - 3}}{{x - 2}} = \dfrac{7}{{6 - 3x}}\)
A. x = 0
B. x = -1
C. \(x = 2\)
D. Không có giá trị nào của x thỏa mãn
Lời giải
Ta có: \(\dfrac{{ - 3}}{{x - 2}} = \dfrac{7}{{6 - 3x}}\) (Điều kiện: \(x - 2 \ne 0;6 - 3x \ne 0 \) hay \(x \ne 2\))
\(\begin{array}{l} - 3.(6 - 3x) = 7.(x - 2)\\ - 18 + 9x = 7x – 14\\9x - 7x = - 14 + 18\\ 2x = 4\end{array}\)
x = 2 ( Loại vì không thỏa mãn điều kiện)
Vậy không tìm được x thỏa mãn điều kiện
Câu 8. Tìm số hữu tỉ x biết rằng \(\dfrac{x}{{{y^2}}} = 2\) và \(\dfrac{x}{y} = 16\) \(\left( {y \ne 0} \right).\)
A. \(x = 16\)
B. \(x = 128\)
C. \(x = 8\)
D. \(x = 256\)
Lời giải
Ta có \(\dfrac{x}{{{y^2}}} = 2\) nên \(\dfrac{x}{y}.\dfrac{1}{y} = 2\), mà \(\dfrac{x}{y} = 16\). Do đó:
\(16.\dfrac{1}{y} = 2\)
\(\dfrac{1}{y} = \dfrac{1}{8}\)
\(y = 8\)
Thay \(y = 8\) vào \(\dfrac{x}{y} = 16\) ta được: \(\dfrac{x}{8} = 16\) nên \(x = 16.8 = 128\).
Đáp án B













Danh sách bình luận