Lý thuyết Nguyên hàm Toán 12 Kết nối tri thức

Lý thuyết Nguyên hàm

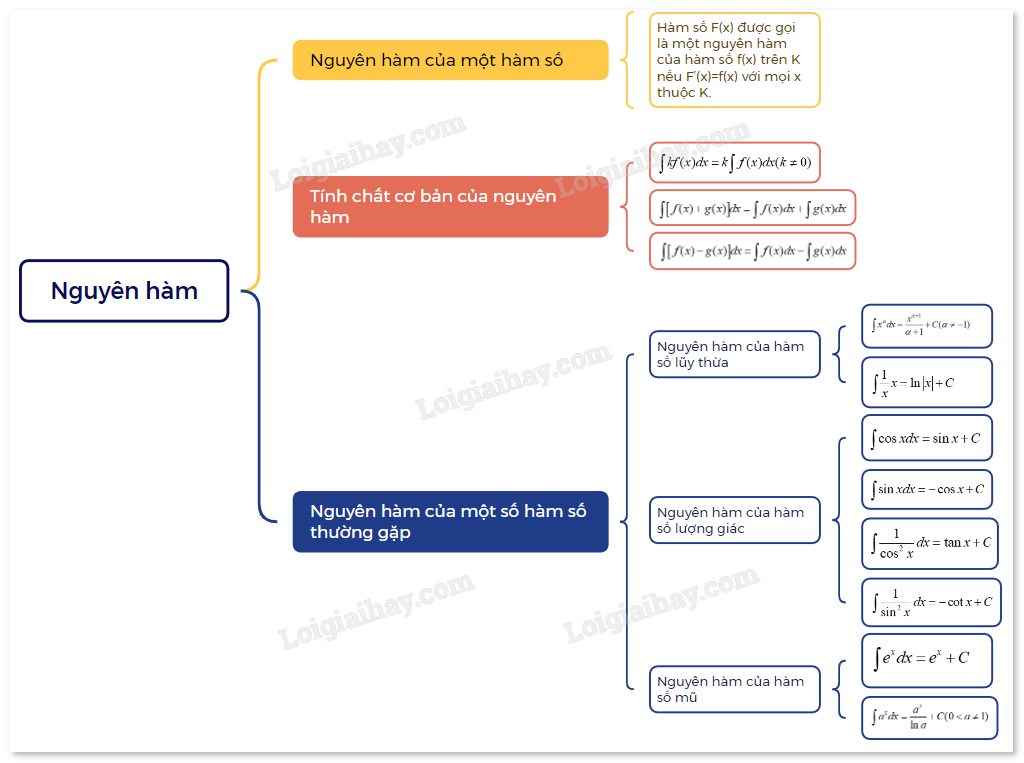
1. Nguyên hàm của một hàm số

Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F’(x)=f(x) với mọi x thuộc K.

Chú ý:

Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:

a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K

b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K

Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + C là họ các nguyên hàm của f(x) trên K, kí hiệu bởi \(\int {f(x)dx} \).

2. Tính chất cơ bản của nguyên hàm

\(\int {kf(x)dx = k\int {f(x)dx(k \ne 0)} } \)
\(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx + \int {g(x)dx} } \)
\(\int {\left[ {f(x) - g(x)} \right]} dx = \int {f(x)dx - \int {g(x)dx} } \)

3. Nguyên hàm của một số hàm số thường gặp

a) Nguyên hàm của hàm số lũy thừa

Hàm số lũy thừa \(y = {x^\alpha }(\alpha \in R)\) có đạo hàm với mọi x > 0 và \(({x^\alpha })' = \alpha {x^{\alpha - 1}}\)

\(\int {{x^\alpha }dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)} \)
\(\int {\frac{1}{x}x = \ln \left| x \right| + C} \)

b) Nguyên hàm của hàm số lượng giác

\(\int {\cos xdx = \sin x + C} \)
\(\int {\sin xdx = - \cos x + C} \)
\(\int {\frac{1}{{{{\cos }^2}x}}dx = \tan x + C} \)
\(\int {\frac{1}{{{{\sin }^2}x}}dx = - \cot x + C} \)

c) Nguyên hàm của hàm số mũ

\(\int {{e^x}dx = {e^x} + C} \)
\(\int {{a^x}dx = \frac{{{a^x}}}{{\ln a}} + C(0 < a \ne 1)} \)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 4,5,6 SGK Toán 12 tập 2 - Kết nối tri thức
Nguyên hàm của một số
Giải mục 2 trang 6,7,8 SGK Toán 12 tập 2 - Kết nối tri thức
Tính chất cơ bản của nguyên hàm
Giải mục 3 trang 8,9,10 SGK Toán 12 tập 2 - Kết nối tri thức
Nguyên hàm của một số hàm số thường gặp
Giải bài tập 4.1 trang 11 SGK Toán 12 tập 2 - Kết nối tri thức
Trong mỗi trường hợp sau, hàm số F(x) có là một nguyên hàm của hàm số f(x) trên khoảng tương ứng không? Vì sao? a) \(F\left( x \right) = x\ln x\) và \(f\left( x \right) = 1 + \ln x\) trên khoảng \(\left( {0; + \infty } \right)\); b) \(F\left( x \right) = {e^{\sin x}}\) và \(f\left( x \right) = {e^{\cos x}}\) trên \(\mathbb{R}\).
Giải bài tập 4.2 trang 11 SGK Toán 12 tập 2 - Kết nối tri thức
Tìm nguyên hàm của các hàm số sau: a) \(f\left( x \right) = 3{x^2} + 2x - 1\); b) \(f\left( x \right) = {x^3} - x\); c) \(f\left( x \right) = {\left( {2x + 1} \right)^2}\); d) \(f\left( x \right) = {\left( {2x - \frac{1}{x}} \right)^2}\).
Giải bài tập 4.3 trang 11 SGK Toán 12 tập 2 - Kết nối tri thức
Tìm: a) \(\int {\left( {3\sqrt x + \frac{1}{{\sqrt[3]{x}}}} \right)} dx\); b) \(\int {\sqrt x \left( {7{x^2} - 3} \right)} dx\left( {x > 0} \right)\); c) \(\int {\frac{{{{\left( {2x + 1} \right)}^2}}}{{{x^2}}}} dx\); d) \(\int {\left( {{2^x} + \frac{3}{{{x^2}}}} \right)} dx\).
Giải bài tập 4.4 trang 11 SGK Toán 12 tập 2 - Kết nối tri thức
Tìm: a) (int {left( {2cos x - frac{3}{{{{sin }^2}x}}} right)} dx); b) (int {4{{sin }^2}frac{x}{2}} dx); c) (int {{{left( {sin frac{x}{2} - cos frac{x}{2}} right)}^2}} dx); d) (int {left( {x + {{tan }^2}x} right)} dx).
Giải bài tập 4.5 trang 11 SGK Toán 12 tập 2 - Kết nối tri thức
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {0; + \infty } \right)\). Biết rằng \(f'\left( x \right) = 2x + \frac{1}{{{x^2}}}\) với mọi \(x \in \left( {0; + \infty } \right)\) và \(f\left( 1 \right) = 1\). Tính giá trị f(4).
Giải bài tập 4.6 trang 11 SGK Toán 12 tập 2 - Kết nối tri thức
Cho hàm số \(y = f\left( x \right)\) có đồ thị là (C). Xét điểm \(M\left( {x;f\left( x \right)} \right)\) thay đổi trên (C). Biết rằng, hệ số góc của tiếp tuyến của đồ thị (C) tại M là \({k_M} = {\left( {x - 1} \right)^2}\) và điểm M trùng với gốc tọa độ khi nó nằm trên trục tung. Tìm biểu thức f(x).
Giải bài tập 4.7 trang 11 SGK Toán 12 tập 2 - Kết nối tri thức
Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm t giây (coi \(t = 0\) là thời điểm viên đạn được bắn lên), vận tốc của nó được cho bởi \(v\left( t \right) = 160 - 9,8t\left( {m/s} \right)\). Tìm độ cao của viên đạn (tính từ mặt đất). a) Sau \(t = 5\) giây; b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất).