-
Toán 9 tập 1 - Cùng khám phá
-
Toán 9 tập 2 - Cùng khám phá
Lý thuyết Hình trụ Toán 9 Cùng khám phá
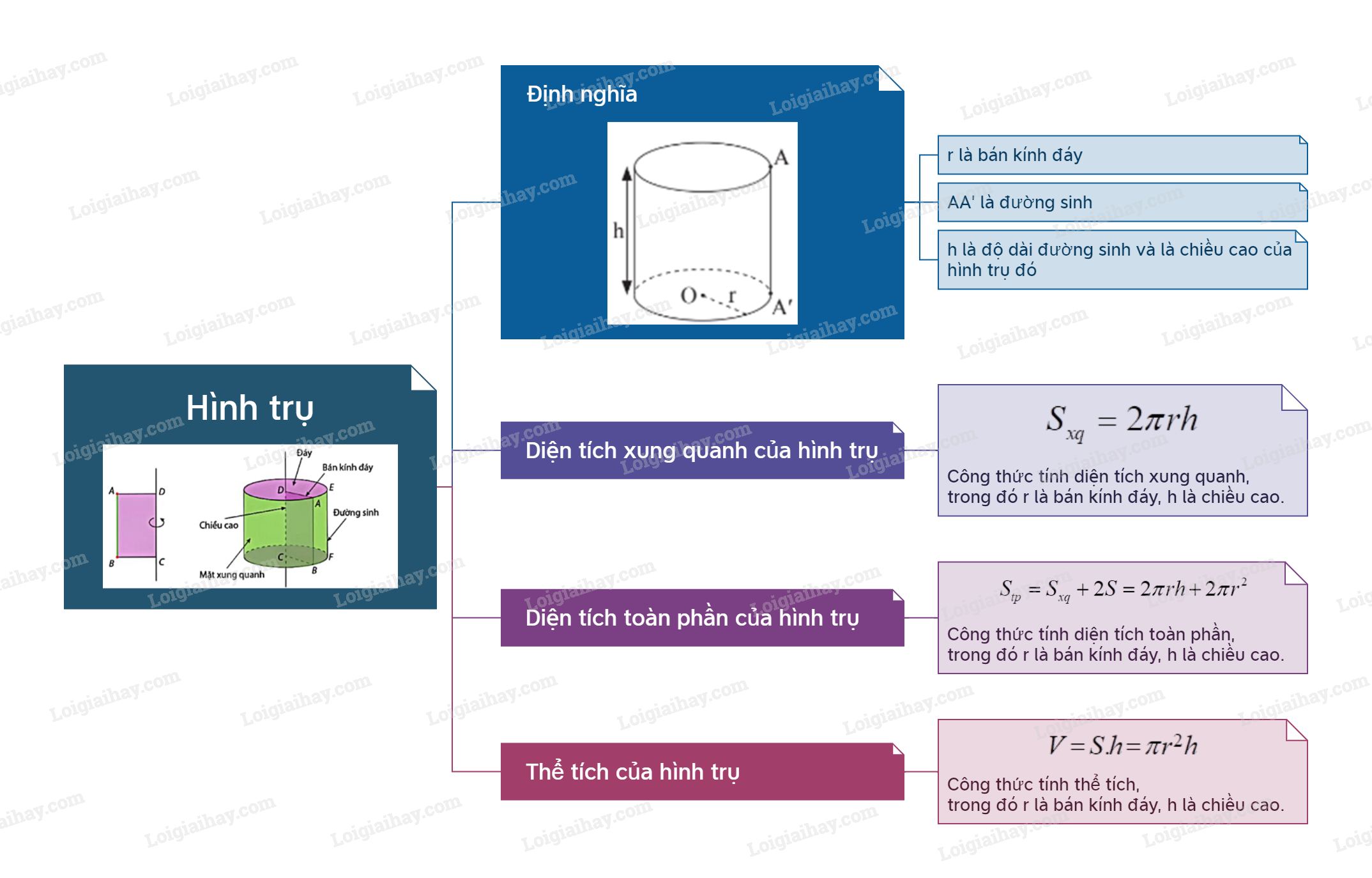
Định nghĩa Ví dụ: Hình trụ trên có: + r là bán kính đáy; + AA’ là đường sinh; + h là độ dài đường sinh và là chiều cao của hình trụ đó.
Định nghĩa
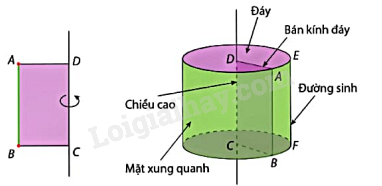
Ví dụ:
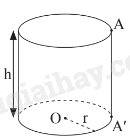
Hình trụ trên có:
+ r là bán kính đáy;
+ AA’ là đường sinh;
+ h là độ dài đường sinh và là chiều cao của hình trụ đó.
2. Diện tích xung quanh của hình trụ
Diện tích xung quanh của hình trụ
|
Diện tích xung quanh \({S_{xq}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{xq}} = 2\pi rh\). |
Diện tích toàn phần của hình trụ
|
Diện tích toàn phần \({S_{tp}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{tp}} = {S_{xq}} + 2S = 2\pi rh + 2\pi {r^2}\) (S là diện tích đáy của hình trụ). |
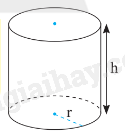
Ví dụ:
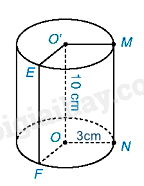
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .3.10 = 60\pi \left( {c{m^2}} \right)\)
3. Thể tích của hình trụ
|
Thể tích V của hình trụ có bán kính đáy r và chiều cao h là: \(V = S.h = \pi {r^2}h\) (S là diện tích đáy của hình trụ).
|
Ví dụ:
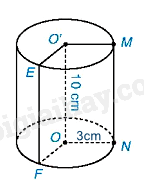
Diện tích đáy là:
\(S = \pi {r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Thể tích của hình trụ là:
\(V = S.h = 9\pi .10 = 90\pi \left( {c{m^3}} \right)\)
Bình luận
Chia sẻ
- Giải mục 1 trang 62, 63 SGK Toán 9 tập 2 - Cùng khám phá
- Giải mục 2 trang 63, 64 SGK Toán 9 tập 2 - Cùng khám phá
- Giải mục 3 trang 65, 66 SGK Toán 9 tập 2 - Cùng khám phá
- Giải mục 4 trang 66, 67 SGK Toán 9 tập 2 - Cùng khám phá
- Giải bài tập 9.1 trang 67 SGK Toán 9 tập 2 - Cùng khám phá
>> Xem thêm
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
