Bài 1. Hình trụ - Toán 9 Cùng khám phá

Giải mục 3 trang 65, 66 SGK Toán 9 tập 2 - Cùng khám phá

Trong một thí nghiệm, bạn Mai thả một khối sắt hình trụ có chiều cao h = 6,5 cm, bán kính đáy r = 3,5 cm vào một bình chia độ đang chứa 500 ml nước. Sau khi khối sắt chìm hẳn xuống, bạn Mai thấy mực nước trong bình tăng lên vạch 750ml. Biết 1 ml = 1 cm3.

Lựa chọn câu để xem lời giải nhanh hơn

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 65 SGK Toán 9 Cùng khám phá

Trong một thí nghiệm, bạn Mai thả một khối sắt hình trụ có chiều cao h = 6,5 cm, bán kính đáy r = 3,5 cm vào một bình chia độ đang chứa 500 ml nước. Sau khi khối sắt chìm hẳn xuống, bạn Mai thấy mực nước trong bình tăng lên vạch 750ml. Biết 1 ml = 1 cm³.

a) Dựa vào mực nước tăng lên trong bình, hãy tính thể tích của khối sắt.

b) Gọi S là diện tích đáy của khối sắt. So sánh tích S.h với kết quả ở câu a và rút ra nhận xét.

Phương pháp giải:

Dựa vào diện tích đường tròn: S = \(\pi {r^2}\) rồi so sánh với câu a.

Lời giải chi tiết:

a) Sự chênh lệch mực nước giữa trước và sau khi cho khối sắt là:

750 – 500 = 250 ml = 250 cm³

Thể tích của khối sắt là 250 cm³.

a) Diện tích đáy của khối sắt là:

S = \(\pi .3,{5^2} = 12,25\) cm²

Suy ra S.h = \(12,25\pi \).6,5 \( \approx 250\) bằng với kết quả câu a

Nhận xét: Thể tích của hình trụ bằng diện tích đáy nhân chiều cao.

LT3

Trả lời câu hỏi Luyện tập 3 trang 66 SGK Toán 9 Cùng khám phá

Tính chiều cao và thể tích của một hình trụ có bán kính đáy bằng 5 cm và diện tích xung quanh bằng \(30\pi \)cm².

Phương pháp giải:

Diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).

Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)

Lời giải chi tiết:

Ta có: \({S_{xq}} = 2\pi rh = 30\pi \)

suy ra h = \(\frac{{30\pi }}{{2\pi .5}} = 3\) cm.

Thể tích hình trụ là:

V = \(\pi {r^2}h = \pi {.5^2}.3 = 75\pi \) (cm³).

VD2

Trả lời câu hỏi Vận dụng 2 trang 66 SGK Toán 9 Cùng khám phá

Tính thể tích nhựa cần dùng để sản xuất đoạn ống nhựa có kích thức như Hình 9.9.

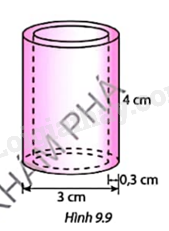
Phương pháp giải:

Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)

Lời giải chi tiết:

Thể tích cả đoạn ống nhựa là:

V = \(\pi {r^2}h = \pi .1,{5^2}.4 = 9c{m^3}\)

Thể tích lõi trong ống nhựa là:

V_lõi\( = \pi {r^2}h = \pi .{\left( {\frac{{3 - 2.0,3}}{2}} \right)^2}.4 = 5,76c{m^3}\)

Thể tích nhựa cần dùng là:

V_nhựa = 9 – 5,76 = 3,24 cm³.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 4 trang 66, 67 SGK Toán 9 tập 2 - Cùng khám phá
Tạo lập hình trụ có bán kính đáy 3 cm và chiều cao 5 cm theo các bước sau: Bước 1: Cắt hai miếng bìa hình tròn có bán kính bằng 3 cm và một miếng bìa hình chữ nhật có chiều rộng 5 cm, chiều dài bằng chu vi của miếng bìa hình tròn vừa cắt (Hình 9.10a) Bước 2: Dùng băng dính để dán các miếng bìa lại để được một hình trụ (Hình 9.10b).
Giải bài tập 9.1 trang 67 SGK Toán 9 tập 2 - Cùng khám phá
Tìm tên gọi thích hợp cho các ô ? trong Hình 9.12.
Giải bài tập 9.2 trang 67 SGK Toán 9 tập 2 - Cùng khám phá
Tìm các số và đơn vị thích hợp trong các ô ? để hoàn thành Bảng 9.1.
Giải bài tập 9.3 trang 68 SGK Toán 9 tập 2 - Cùng khám phá
Từ một tấm bìa hình chữ nhật với đồ dài hai cạnh là 20 cm, 15 cm có thể cuộn lại và dùng băng dính dán thành hình trụ A hoặc hình trụ B (không có nắp) như Hình 9.13. a) Hãy so sánh thể tích của hai hình trụ A và B. Giải thích câu trả lời của em. b) Nếu cắt tấm bìa thành hai phần X, Y bằng nhau và tạo thành hai hình trụ (không có nắp) cùng chiều cao 15 cm thì tổng thể tích của hai hình trụ này có lớn hơn thể tích của hình trụ B không? Vì sao?
Giải bài tập 9.4 trang 68 SGK Toán 9 tập 2 - Cùng khám phá
Một cái thớt gỗ hình trụ có đường kính đáy 40 cm, dày 5 cm như Hình 9.14. a) Tính thể tích gỗ cần dùng để làm thớt. b) Khối lượng riêng của gỗ làm thớt là D = 500 kg/m3. Hỏi cái thớt nặng bao nhiêu gam (làm tròn đến hàng phần mười), biết khối lượng m (kg) của một vật có thể tích V (m3) là m = D.V?
Giải bài tập 9.5 trang 68 SGK Toán 9 tập 2 - Cùng khám phá
Hình 9.15 là một tủ chứa đồ. Biết cung CDE là nửa đường tròn. a) Tính thể tích của tủ đồ. b) Người ta muốn sơn tất cả các mặt ngoài của tủ (kể cả đáy). Hỏi diện tích cần sơn là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Giải mục 2 trang 63, 64 SGK Toán 9 tập 2 - Cùng khám phá
Một hộp hình trụ làm bằng thiếc có bán kính 5 cm, chiều cao 8 cm (Hình 9.4a). Nếu cắt rời hai đáy và cắt dọc theo đường sinh AB của hộp, rồi trải phẳng ra, ta được hình khai triển của hình trụ (Hình 9.4b). a) Tính chu vi mỗi đáy của hình trụ. b) Tính diện tích miếng thiếc hình chữ nhật để làm thành mặt xung quanh của hộp (diện tích các mối nối không đáng kể).
Giải mục 1 trang 62, 63 SGK Toán 9 tập 2 - Cùng khám phá
Bước 1: Vẽ và cắt một hình chữ nhật ABCD bằng bìa cứng. Đánh dấu hai điểm A và B trên hình chữ nhật bằng màu đỏ và tô đậm đoạn thẳng AB bằng màu xanh. Bước 2: Dùng băng dính hai mặt để dán mép hình chữ nhật này vào một nẹp gỗ dọc theo cạnh CD. Bước 3: Giữ cố định vị trí nẹp gỗ và quay hình chữ nhật ABCD quanh nẹp gỗ. Khi hình chữ nhật ABCD quay quanh nẹp gỗ, hai điểm màu đỏ A và B chuyển động theo đường gì? Đoạn thẳng màu xanh AB quét tạo thành bề mặt của hình gì?
Lý thuyết Hình trụ Toán 9 Cùng khám phá
Định nghĩa Ví dụ: Hình trụ trên có: + r là bán kính đáy; + AA’ là đường sinh; + h là độ dài đường sinh và là chiều cao của hình trụ đó.