Bài 5. Góc ở tâm, cung và hình quạt tròn - Toán 9 Cùng ..

Lý thuyết Góc ở tâm, cung và hình quạt tròn Toán 9 Cùng khám phá

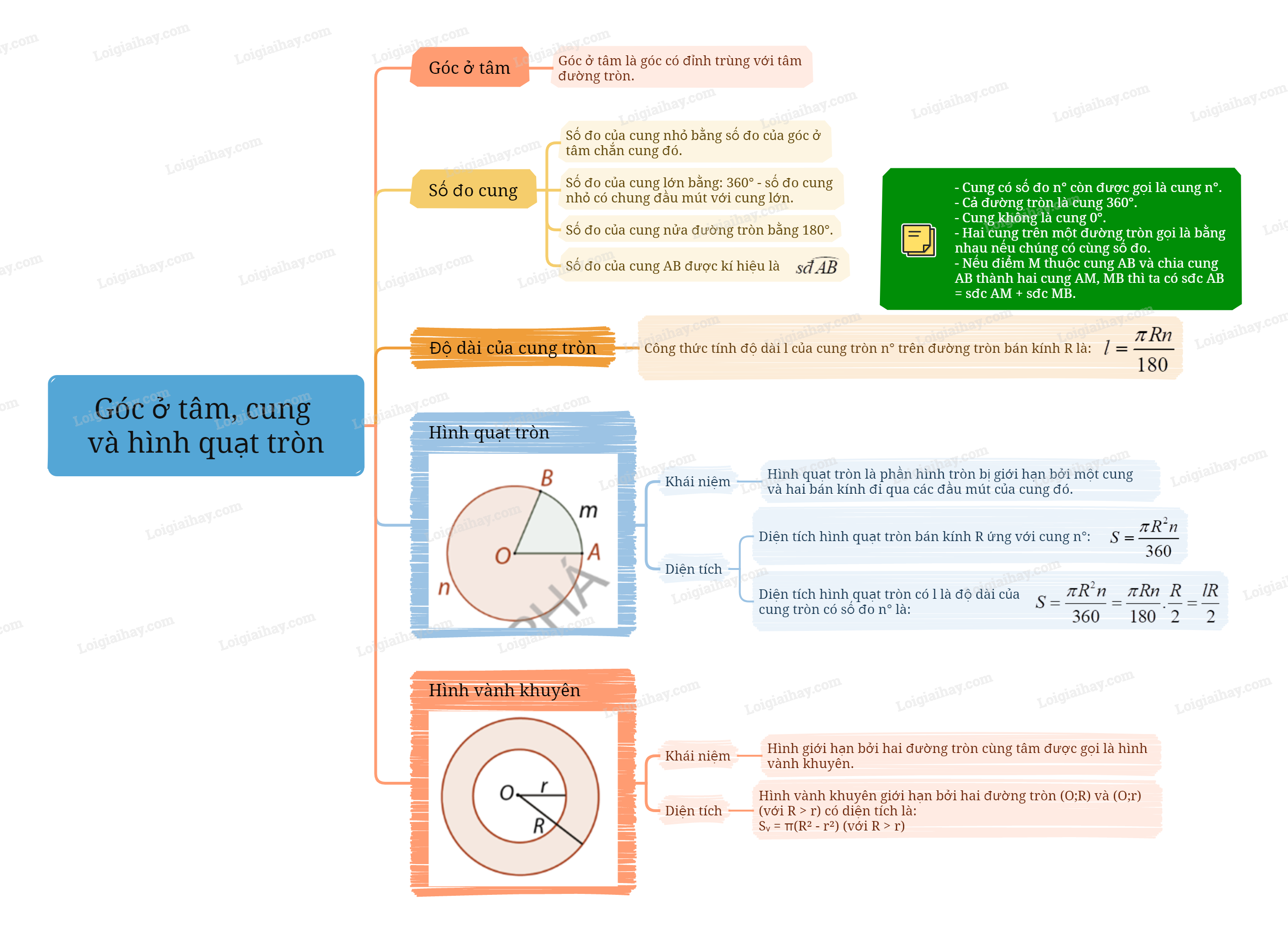
1. Góc ở tâm và số đo cung Góc ở tâm Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm của đường tròn. Số đo cung

1. Góc ở tâm và số đo cung

Góc ở tâm

Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm của đường tròn.

Số đo cung

Trong đường tròn:

- Số đo của cung nhỏ là số đo của góc ở tâm chắn cung đó;

- Số đo của cung lớn là hiệu giữa ${360^0}$ và số đo của cung nhỏ cùng đầu mút với nó.

- Số đo của nửa đường tròn là ${180^0}$.

Lưu ý: Trong một đường tròn:

- Số đo của cung AB được kí hiệu là sđ$\overset\frown{AB}$.

- Các cung có số đo bằng ${n^0}$ được gọi chung là cung ${n^0}$. Mỗi điểm trên đường tròn được xem là một cung ${0^0}$, cả đường tròn được xem là cung ${360^0}$.

- Tổng số đo hai cung có chung đầu mút là ${360^0}$.

- Nếu điểm M thuộc cung AB và chia cung AB thành hai cung AM, MB thì ta có sđ$\overset\frown{AB}$ = sđ$\overset\frown{AM}$ + sđ$\overset\frown{MB}$.

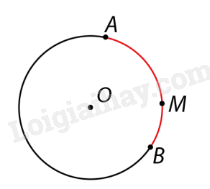
2. Độ dài cung

Công thức độ dài cung ${n^0}$ của đường tròn bán kính R:

$l = \frac{{\pi Rn}}{{180}}$.

Ví dụ:

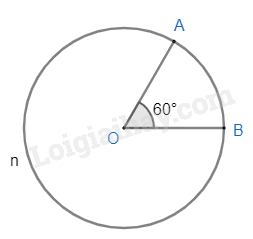
Đường tròn (O; 2cm), $\widehat {AOB} = {60^0}$.

- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.

Do đó sđ$\overset\frown{AB}=\widehat{AOB}={{60}^{0}}$.

Độ dài ${l_1}$ của cung AB là:

${l_1} = \frac{n}{{180}}\pi R = \frac{{60}}{{180}}\pi .2 = \frac{{2\pi }}{3} \approx 2,1\left( {cm} \right)$

Cung lớn AnB có số đo là:

sđ$\overset\frown{AmN}={{360}^{o}}-{{60}^{0}}={{300}^{0}}$.

Độ dài ${l_2}$ của cung AnB là:

${l_2} = \frac{{300}}{{180}}\pi .2 = \frac{{10}}{3}\pi \approx 10,5\left( {cm} \right)$

3. Diện tích hình quạt tròn và hình vành khuyên

Khái niệm hình quạt tròn

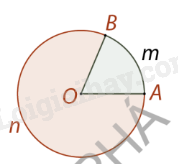
Hình quạt tròn là phần hình tròn bị giới hạn bởi một cung và hai bán kính đi qua các đầu mút của cung đó.

Diện tích hình quạt tròn

Nếu ${S_q}$ là phần diện tích của hình quạt tròn bán kính R ứng với cung có số đo ${n^0}$ thì:

$\frac{{{S_q}}}{{\pi {R^2}}} = \frac{n}{{360}}$.

Công thức diện tích hình quạt tròn bán kính R ứng với cung ${n^o}$:

${S_q} = \frac{{\pi {R^2}n}}{{360}}$

Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là $l = 4\pi $cm, bán kính là R = 5cm là:

${S_q} = \frac{{l.R}}{2} = \frac{{4\pi .5}}{2} = 10\pi \left( {c{m^2}} \right)$

Khái niệm hình vành khuyên

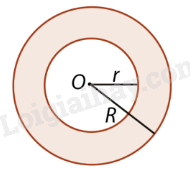
Hình vành khuyên là hình giới hạn bởi hai đường tròn đồng tâm có bán kính khác nhau.

Diện tích hình vành khuyên

Công thức diện tích hình vành khuyên tạo bởi hai đường tròn (O;R) và (O;r) (với r < R):

${S_v} = \pi \left( {{R^2} - {r^2}} \right)$.

Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:

${S_v} = \pi \left( {{5^2} - {3^2}} \right) = 16\pi \left( {{m^2}} \right)$

Lưu ý: Từ công thức tính diện tích hình quạt tròn và độ dài cung ${n^0}$, bán kính R, ta có công thức liên hệ hai diện tích hình quạt (${S_q}$) với độ dài cung ($l$) ứng với nó như sau:

${S_q} = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi Rn}}{{180}}.\frac{R}{2} = \frac{1}{2}lR$.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải câu hỏi khởi động trang 115 SGK Toán 9 tập 1 - Cùng khám phá
Vì sao để chia một chiếc bánh ngọt có mặt hình tròn thành nhiều phần bằng nhau, người ta thường cắt bánh thành các đường đi qua tâm bánh (Hình 5.43)?
Giải mục 1 trang 115, 116, 117 SGK Toán 9 tập 1 - Cùng khám phá
Cắt một hình tròn bằng giấy và gấp làm hai, làm tư, làm tám như trong Hình 5.45. 1. Cho biết giao điểm O của các đường gấp ở đâu trong hình tròn? 2. Các đường gấp chia hình tròn thành nhiều phần. Trong mỗi trường hợp, hãy: a) Cho biết khi đường tròn (O) được gấp lại, các cung của đường tròn nằm trong các phần chồng khít lên nhau không? b) So sánh số đo các góc đỉnh O trong mỗi phần và tính tổng số đo các góc đỉnh O trong tất cả các phần.
Giải mục 2 trang 117, 118, 119 SGK Toán 9 tập 1 - Cùng khám phá
Cắt một hình tròn bằng giấy và đánh dấu hai điểm A, B bất kì trên mép của hình tròn. a) Sử dụng dây mềm để lần lượt viền theo hai cung AB như Hình 5.49a và đo độ dài của đoạn dây trong mỗi trường hợp. b) Lấy một điểm M bất kì trên cung AB, chia cung AB thành hai cung AM và MB. So sánh tổng độ dài hai đoạn dây được viền theo cung AB và MB với độ dài đoạn dây được viền theo cung AB (Hình 5.49b).
Giải mục 3 trang 119, 120, 121 SGK Toán 9 tập 1 - Cùng khám phá
Quay lại hoạt động gấp hình tròn trong Hoạt động 1. Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?
Giải bài tập 5.22 trang 121 SGK Toán 9 tập 1 - Cùng khám phá
Vẽ đường tròn (O), sau đó vẽ: a) Một góc ở tâm của (O) có số đo ${50^o}$; b) Một cung có số đo ${235^o}$.
Giải bài tập 5.23 trang 121 SGK Toán 9 tập 1 - Cùng khám phá
Cho điểm A thuộc đường tròn (O). Trên tiếp tuyến tại A của (O) xác định điểm M sao cho $AM = AO$. Đường thẳng OM cắt (O) tại B và C (B nằm giữa O và M). a) Tính góc ở tâm BOA. b) Tính số đo cung lớn AC.
Giải bài tập 5.24 trang 121 SGK Toán 9 tập 1 - Cùng khám phá
Tiếp tuyến tại hai điểm A và B của đường tròn (O) cắt nhau tại M. Biết rằng MAB là tam giác đều. Tính số đo cung nhỏ và cung lớn AB.
Giải bài tập 5.25 trang 121 SGK Toán 9 tập 1 - Cùng khám phá
Trong 20 giây, kim giây của đồng hồ quay được một cung có số đo bằng bao nhiêu (Hình 5.55)?
Giải bài tập 5.26 trang 121 SGK Toán 9 tập 1 - Cùng khám phá
Tính chu vi và diện tích phần được tô màu trong mỗi trường hợp ở Hình 5.56. Làm tròn kết quả đến hàng phần mười.
Giải bài tập 5.27 trang 122 SGK Toán 9 tập 1 - Cùng khám phá
Trong Hình 5.57, bia bắn cung có dạng hình tròn bán kính 20cm. Bia được chia thành năm phần bởi bốn đường tròn có bán kính lần lượt 4cm, 8cm, 12cm, 16cm. Mỗi phần được sơn một màu khác nhau. Tính diện tích mỗi phần.
Giải bài tập 5.28 trang 122 SGK Toán 9 tập 1 - Cùng khám phá
Trong Hình 5.58, bánh pizza có dạng hình tròn tâm O được cắt thành sáu phần bằng nhau. Góc AOB có số đo bằng bao nhiêu?
Giải bài tập 5.29 trang 122 SGK Toán 9 tập 1 - Cùng khám phá
Một chiếc xe lu có đường kính trống lu là 1,5m và đường kính của bánh sau là 1,2m (Hình 5.59). Khi hoạt động, trống lu quay hết một vòng $\left( {{{360}^o}} \right)$ trong 5 phút. a) Trong mỗi phút, trống lu quay được bao nhiêu độ và xe lu cán được bao nhiêu mét đường? b) Để cán được 1 mét đường thì trống lu phải quay một góc bao nhiêu độ? c) Để trống lu quay được 1 vòng thì bánh sau phải quay bao nhiêu vòng?