-
Toán 9 tập 1 - Cánh diều
-
Toán 9 tập 2 - Cánh diều
Toán 9 cánh diều | Giải toán lớp 9 cánh diều
Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội t..
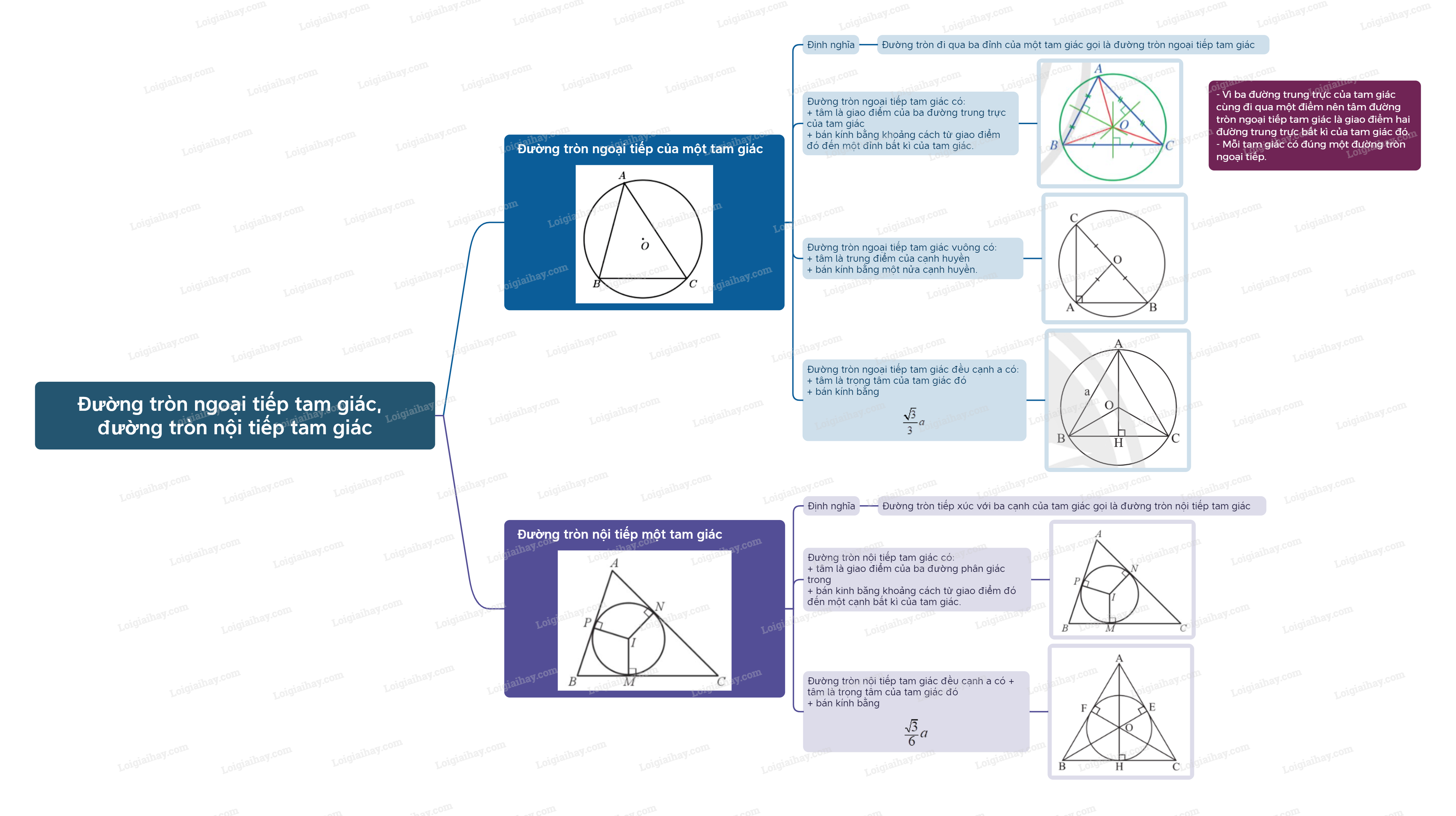
Lý thuyết Đường tròn ngoại tiếp tam giác, đường tròn nội tiếp tam giác Toán 9 Cánh diều
1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác đó.
Tổng hợp đề thi giữa kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
1. Đường tròn ngoại tiếp tam giác
Định nghĩa đường tròn ngoại tiếp tam giác
|
Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác đó. |
Xác định tâm và bán kính đường tròn ngoại tiếp tam giác
|
Tâm đường tròn ngoại tiếp tam giác là giao điểm ba đường trung trực của tam giác đó. Bán kính đường tròn ngoại tiếp tam giác bằng khoảng cách từ giao điểm ba đường trung trực đến mỗi đỉnh của tam giác đó.
|
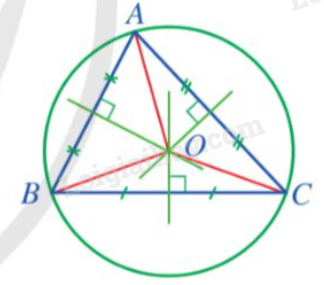
Ví dụ:
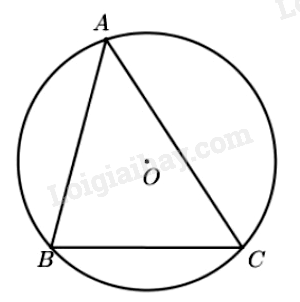
- Đường tròn (O) ngoại tiếp tam giác ABC. Tam giác ABC nội tiếp đường tròn (O).
- Tâm O là giao điểm của ba đường trung trực của tam giác ABC.
Nhận xét:
- Vì ba đường trung trực của tam giác cùng đi qua một điểm nên tâm đường tròn ngoại tiếp tam giác là giao điểm hai đường trung trực bất kì của tam giác đó.
- Mỗi tam giác có đúng một đường tròn ngoại tiếp.
Đường tròn ngoại tiếp tam giác vuông
|
Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng một nửa cạnh huyền.
|
Ví dụ:
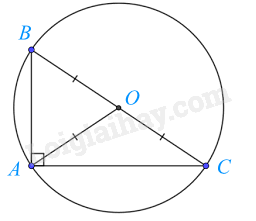
Tam giác ABC nội tiếp đường tròn (O; BO).
Đường tròn ngoại tiếp tam giác đều
|
- Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm đường tròn ngoại tiếp của tam giác đó. - Tam giác đều cạnh a có bán kính đường tròn ngoại tiếp là \(R = \frac{{a\sqrt 3 }}{3}\).
|
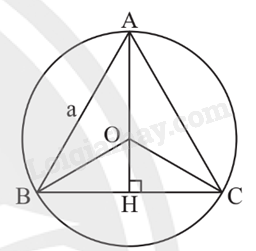
Ví dụ:
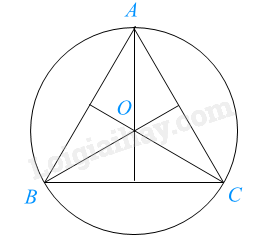
Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\).
2. Đường tròn nội tiếp một tam giác
Định nghĩa đường tròn nội tiếp tam giác
|
Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác đó. |
Xác định tâm và bán kính đường tròn ngoại tiếp tam giác
|
- Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác của tam giác đó. - Bán kính đường tròn nội tiếp tam giác bằng khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh của tam giác đó. |
Ví dụ:
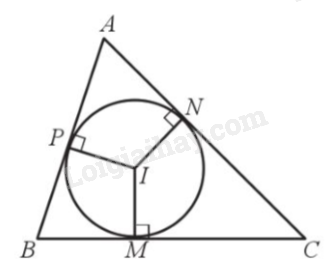
- Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I).
- Tâm I là giao điểm của ba đường phân giác của tam giác.
Nhận xét:
- Vì ba đường phân giác của một tam giác cùng đi qua một điểm nên tâm đường tròn nội tiếp là giao điểm hai đường phân giác bất kì của tam giác đó.
- Mỗi tam giác có đúng một đường tròn nội tiếp.
Đường tròn nội tiếp tam giác đều
|
- Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm đường tròn nội tiếp tam giác đó. - Tam giác đều cạnh a có bán kính đường tròn nội tiếp là \(r = \frac{{a\sqrt 3 }}{6}\).
|
Ví dụ:
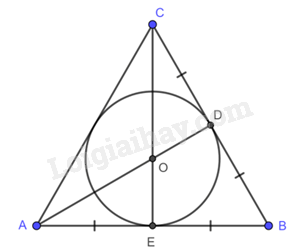
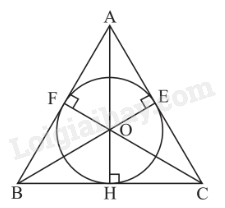
Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\).
Bình luận
Chia sẻ
- Giải mục 1 trang 68, 69, 70 SGK Toán 9 tập 2 - Cánh diều
- Giải mục 2 trang 71, 72, 73 SGK Toán 9 tập 2 - Cánh diều
- Giải bài tập 1 trang 73 SGK Toán 9 tập 2 - Cánh diều
- Giải bài tập 2 trang 74 SGK Toán 9 tập 2 - Cánh diều
- Giải bài tập 3 trang 74 SGK Toán 9 tập 2 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
