Giải bài tập 5 trang 74 SGK Toán 9 tập 2 - Cánh diều

Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O) đường kính AD = 2R. Gọi M là trung điểm của cạnh BC và H là trực tâm của tam giác ABC. Chứng minh: a) (BD bot AB,CD bot AC.) b) Tứ giác BHCD là hình bình hành. c) (A{C^2} + B{H^2} = 4{R^2}.) d) Ba điểm H, M, D thẳng hàng và AH = 2OM.

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Cánh diều

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O) đường kính AD = 2R. Gọi M là trung điểm của cạnh BC và H là trực tâm của tam giác ABC. Chứng minh:

a) \(BD \bot AB,CD \bot AC.\)

b) Tứ giác BHCD là hình bình hành.

c) \(A{C^2} + B{H^2} = 4{R^2}.\)

d) Ba điểm H, M, D thẳng hàng và AH = 2OM.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Dựa vào định lý: Trong một tam giác có đường trung tuyến ứng với một cạnh và bằng nửa cạnh ấy thì tam giác đó vuông.

b) Chứng minh BH//CD, HC//BD thông qua mối quan hệ từ vuông góc đến song song.

c) Áp dụng định lý Pytago trong tam giác vuông ACD.

d) H, M, D thẳng hàng: Chỉ ra M là giao điểm của 2 đường chéo trong hình bình hành BHCD.

AH = 2OM: Chứng minh OM là đường trung bình của tam giác AHD.

Lời giải chi tiết

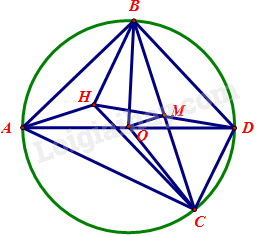
a) Chứng minh: \(BD \bot AB\)

Vì tam giác ABD nội tiếp đường tròn (O) nên AO = OB = OD Mà AD là đường kính của (O) suy ra \(OA = OD = \frac{{AD}}{2}.\)

Do đó \(OB = OA = OD = \frac{{AD}}{2}.\)

Xét tam giác ABD có đường trung tuyến BO và \(OB = \frac{{AD}}{2}\) nên tam giác ABD vuông tại B, suy ra \(BD \bot AB\)

Chứng minh: \(CD \bot AC.\)

Vì tam giác ACD nội tiếp đường tròn (O) nên AO = OC = OD Mà AD là đường kính của (O) suy ra \(OA = OD = \frac{{AD}}{2}.\)

Do đó \(OC = OA = OD = \frac{{AD}}{2}.\)

Xét tam giác ACD có đường trung tuyến CO và \(OC = \frac{{AD}}{2}\) nên tam giác ACD vuông tại C, suy ra \(CD \bot AC.\)

b) Ta có: H là trực tâm của tam giác ABC nên \(BH \bot AC\),\(CH \bot AB\)

Ta lại có:

\(BH \bot AC\), \(CD \bot AC\)(câu a) nên BH // DC.

\(CH \bot AB\), \(BD \bot AB\) (câu a) nên CH // BD.

Xét BHCD có: BH // DC, CH // BD (cmt) suy ra BHCD là hình bình hành (dhnb).

c) Do BHCD là hình bình hành nên BH = CD.

Xét tam giác ADC vuông tại C có: \(A{C^2} + C{D^2} = A{D^2}\), mà BH = CD, AD = 2R nên:

\(A{C^2} + B{H^2} = 4{R^2}\).

d) Do BHCD là hình bình hành, M là trung điểm của đường chéo BC nên M cũng là trung điểm của đường chéo HD. Hay H, M, D thẳng hàng.

Xét tam giác AHD có: M là trung điểm của HD (cmt), O là trung điểm của AD nên OM là đường trung bình, suy ra \(OM = \frac{1}{2}AH\) hay \(AH = 2OM.\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 6 trang 74 SGK Toán 9 tập 2 - Cánh diều
Cho tứ giác ABCD có các tam giác ABC và ACD lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17). Chứng minh: a) Ba điểm I, H, K thẳng hàng. b) AM = AN. c) (widehat {IAK} = frac{1}{2}widehat {BAD}.)
Giải bài tập 4 trang 74 SGK Toán 9 tập 2 - Cánh diều
Một chiếc máy quay ở đài truyền hình được đặt trên giá đỡ 3 chân, các điểm tiếp xúc với mặt đất của 3 chân lần lượt là 3 đỉnh A, B, C của tam giác đều ABC (Hình 16). Tính khoảng cách giữa 2 vị trí A và B, biết bán kính đường tròn ngoại tiếp tam giác ABC là 4 dm.
Giải bài tập 3 trang 74 SGK Toán 9 tập 2 - Cánh diều
Cho bán kính đường tròn nội tiếp tam giác đều bằng 4cm. Tính cạnh của tam giác đều đó.
Giải bài tập 2 trang 74 SGK Toán 9 tập 2 - Cánh diều
Tính bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A với AB = 5cm, AC = 12cm.
Giải bài tập 1 trang 73 SGK Toán 9 tập 2 - Cánh diều
Trong các hình 15a, 15b, 15c, 15d ở hình nào ta có đường tròn (O) là đường tròn ngoại tiếp tam giác ABC? Ở hình nào ta có đường tròn (O) là đường tròn nội tiếp tam giác ABC? Vì sao?
Giải mục 2 trang 71, 72, 73 SGK Toán 9 tập 2 - Cánh diều
Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).
Giải mục 1 trang 68, 69, 70 SGK Toán 9 tập 2 - Cánh diều
Cho biết các đỉnh của tam giác ABC (Hình 2) có thuộc đường tròn (O) hay không?
Lý thuyết Đường tròn ngoại tiếp tam giác, đường tròn nội tiếp tam giác Toán 9 Cánh diều
1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác đó.