Vật lí lớp 12 Nâng cao

Bài 21. Dao động điện từ

Lý thuyết dao động điện từ

Bình chọn:

4.9 trên 7 phiếu

DAO ĐỘNG ĐIỆN TỪ 1. Dao động điện từ trong mạch LC

Xem thêm: Bài 21. Dao động điện từ

DAO ĐỘNG ĐIỆN TỪ

1. Dao động điện từ trong mạch LC

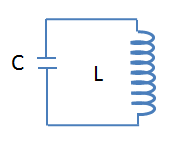
- Mạch LC

- Điện tích (q), dòng điện (i) và điện áp (u) đều biến thiên tuần hoàn theo quy luật dạng sin

\(\begin{array}{l}q = {q_0}cos\left( {\omega t + \varphi } \right)\\i = q' = - \omega {q_0}\sin \left( {\omega t + \varphi } \right) = \omega {q_0}cos\left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\\ = {I_0}cos\left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\\u = \dfrac{q}{C} = \dfrac{{{q_0}}}{C}cos\left( {\omega t + \varphi } \right)\end{array}\)

- Các đặc trưng riêng của mạch LC:

+ Tần số góc riêng: \(\omega = \dfrac{1}{{\sqrt {LC} }}\)

+ Chu kì riêng: \(T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {LC} \)

+ Tần số riêng: \(f = \dfrac{1}{T} = \dfrac{1}{{2\pi \sqrt {LC} }}\)

2. Năng lượng điện từ trong mạch dao động

+ Năng lượng điện trường tập trung trong tụ điện: \({{\rm{W}}_C} = \dfrac{1}{2}\dfrac{{{q^2}}}{C} = \dfrac{1}{2}C{u^2}\)

+ Năng lượng từ trường tập trung trong cuộn cảm: \({{\rm{W}}_L} = \dfrac{1}{2}L{i^2}\)

Năng lượng điện từ: \({\rm{W}} = {{\rm{W}}_C} + {{\rm{W}}_L} = \dfrac{{q_0^2}}{{2C}} = \dfrac{{LI_0^2}}{2} = const\)

3. Dao động điện từ tắt dần – Dao động điện từ duy trì. Hệ tự dao động – Dao động điện từ cưỡng bức. Sự cộng hưởng

- Dao động điện từ tắt dần: Thông thường trong mạch dao động luôn tồn tại điện trở R trên cuộn dây và dây nối.

Do mất mát năng lượng => Hệ dao động tắt dần

- Dao động điện từ duy trì. Hệ tự dao động: Mạch dao động duy trì sẽ cung cấp một phần năng lượng đúng bằng phần năng lượng mất mát trong mỗi giai đoạn (khi có I giảm) của mỗi chu kì

- Dao động điện từ cưỡng bức. Sự cộng hưởng: Khi có nguồn xoay chiều mắc vào mạch thì q, i, u đều dao động theo tần số của nguồn xoay chiều \(\left( \Omega \right)\)

+ Khi \(\Omega = {\omega _0}\): Hệ xảy ra cộng hưởng.