-
Toán 9 tập 1 - Chân trời sáng tạo
-
Toán 9 tập 2 - Chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc ha..
Lý thuyết Biến đổi đơn giản biểu thức chứa căn thức bậc hai Toán 9 Chân trời sáng tạo
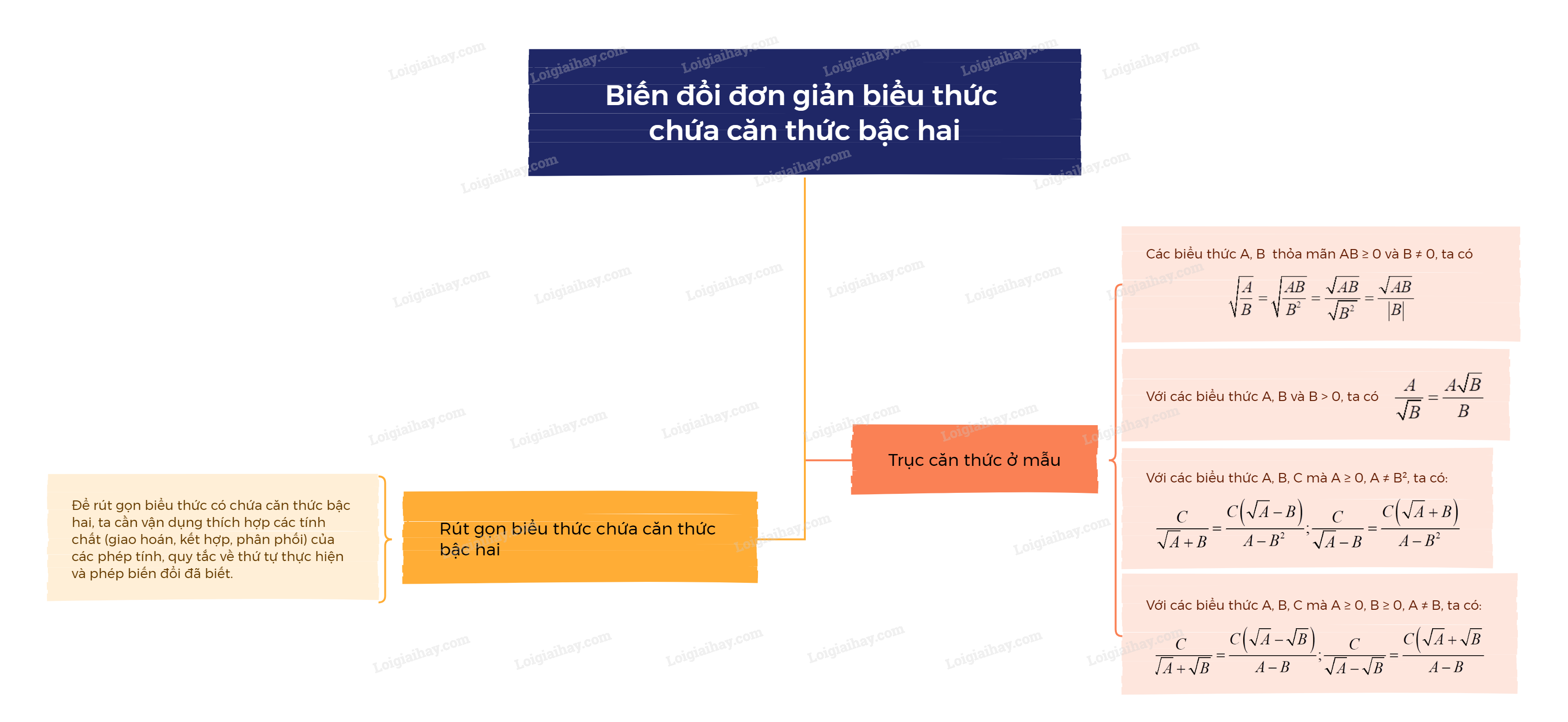
1. Trục căn thức ở mẫu - Với các biểu thức A và B thỏa mãn \(AB \ge 0,B \ne 0\), ta có: \(\sqrt {\frac{A}{B}} = \sqrt {\frac{{AB}}{{{B^2}}}} = \frac{{\sqrt {AB} }}{{\sqrt {{B^2}} }} = \frac{{\sqrt {AB} }}{{\left| B \right|}}\). - Với các biểu thức A, B và B > 0, ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\). - Với các biểu thức A, B, C mà \(A \ge 0,A \ne {B^2}\), ta có: \(\frac{C}{{\sqrt A + B}} = \frac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\frac{C}{{\sqrt A - B}} = \f
Tổng hợp đề thi giữa kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Khoa học tự nhiên
1. Trục căn thức ở mẫu
|
- Với các biểu thức A và B thỏa mãn \(AB \ge 0,B \ne 0\), ta có: \(\sqrt {\frac{A}{B}} = \sqrt {\frac{{AB}}{{{B^2}}}} = \frac{{\sqrt {AB} }}{{\sqrt {{B^2}} }} = \frac{{\sqrt {AB} }}{{\left| B \right|}}\). - Với các biểu thức A, B và B > 0, ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\). - Với các biểu thức A, B, C mà \(A \ge 0,A \ne {B^2}\), ta có: \(\frac{C}{{\sqrt A + B}} = \frac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\frac{C}{{\sqrt A - B}} = \frac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}\). - Với các biểu thức A, B, C mà \(A \ge 0,B \ge 0,A \ne B\), ta có: \(\frac{C}{{\sqrt A + \sqrt B }} = \frac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}};\frac{C}{{\sqrt A - \sqrt B }} = \frac{{C\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}\). |
Ví dụ:
\(\frac{2}{{3\sqrt 5 }} = \frac{{2\sqrt 5 }}{{3{{\left( {\sqrt 5 } \right)}^2}}} = \frac{{2\sqrt 5 }}{{3.5}} = \frac{{2\sqrt 5 }}{{15}}\);
\(\frac{a}{{3 - 2\sqrt 2 }} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{\left( {3 - 2\sqrt 2 } \right).\left( {3 + 2\sqrt 2 } \right)}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{{3^2} - {{\left( {2\sqrt 2 } \right)}^2}}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{9 - 8}} = \left( {3 + 2\sqrt 2 } \right)a\).
2. Rút gọn biểu thức chứa căn thức bậc hai
|
Để rút gọn biểu thức có chứa căn thức bậc hai, ta cần vận dụng thích hợp các tính chất (giao hoán, kết hợp, phân phối) của các phép tính, quy tắc về thứ tự thực hiện và phép biến đổi đã biết. |
Ví dụ:
\(\begin{array}{l}A = 2\sqrt 3 - \sqrt {75} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} \\ = 2\sqrt 3 - \sqrt {{{3.5}^2}} + \left| {1 - \sqrt 3 } \right|\\ = 2\sqrt 3 - 5\sqrt 3 + \sqrt 3 - 1\\ = - 1 - 2\sqrt 3 \end{array}\)
\(\begin{array}{l}B = x\sqrt x - \frac{{{x^2} - x}}{{\sqrt x + 1}}\\ = x\sqrt x - \frac{{\left( {{x^2} - x} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\ = x\sqrt x - \frac{{x\left( {x - 1} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\ = x\sqrt x - \frac{{x\left( {x - 1} \right)\left( {\sqrt x - 1} \right)}}{{x - 1}}\\ = x\sqrt x - x\left( {\sqrt x - 1} \right)\\ = x\sqrt x - x\sqrt x + x\\ = x\end{array}\)
Bình luận
Chia sẻ
- Giải mục 1 trang 52, 53, 54 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải mục 2 trang 54, 55, 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 1 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 2 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 3 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
