 Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
 Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc ha..
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc ha..
Giải bài tập 8 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.
Đề bài
Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.
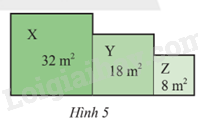
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Từ diện tích S = a2 (a: độ dài cạnh) từng hình vuông ta tìm được lần lượt cạnh của từng hình vuông
- Sau đó tính chu vi của từng hình vuông rồi cộng cá kết quả với nhau.
Lời giải chi tiết
Gọi các điểm trên hình mô tả vườn hoa như hình vẽ.
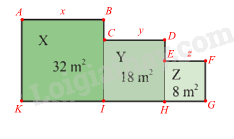
Độ dài cạnh hình vuông X là: \(x = \sqrt {32} = 4\sqrt 2 \)m
Độ dài cạnh hình vuông Y là: \(y = \sqrt {18} = 3\sqrt 2 \)m
Ta có cạnh hình vuông Z là: \(z = \sqrt 8 = 2\sqrt 2 \)m
Quan sát hình vẽ ta thấy: AK = BC + DE + FG hay x = BC + DE + FG
Chu vi của vườn hoa là:
\(AB + BC + CD + DE + EF + FG + GH + HI + IK + KA \)
\(= (AB + IK + AK) + (BC + DE + FG) + (CD + HI) + (EF + GH)\)
\(= 3x + x + 2y + 2z\)
\( = 4x + 2y + 2z\)
\( = 4.4\sqrt 2 + 2.3\sqrt 2 + 2.2\sqrt 2 = 26\sqrt 2 (m)\)
Vậy chu vi của vườn hoa đó là: \(26\sqrt 2 \)m.
- Giải bài tập 7 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 6 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 5 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 4 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 3 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay












Danh sách bình luận