Toán 11, giải toán lớp 11 chân trời sáng tạo Bài 3. Hai mặt phẳng vuông góc Toán 11 Chân trời sáng tạo

Giải mục 4 trang 69, 70, 71 SGK Toán 11 tập 2 - Chân trời sáng tạo


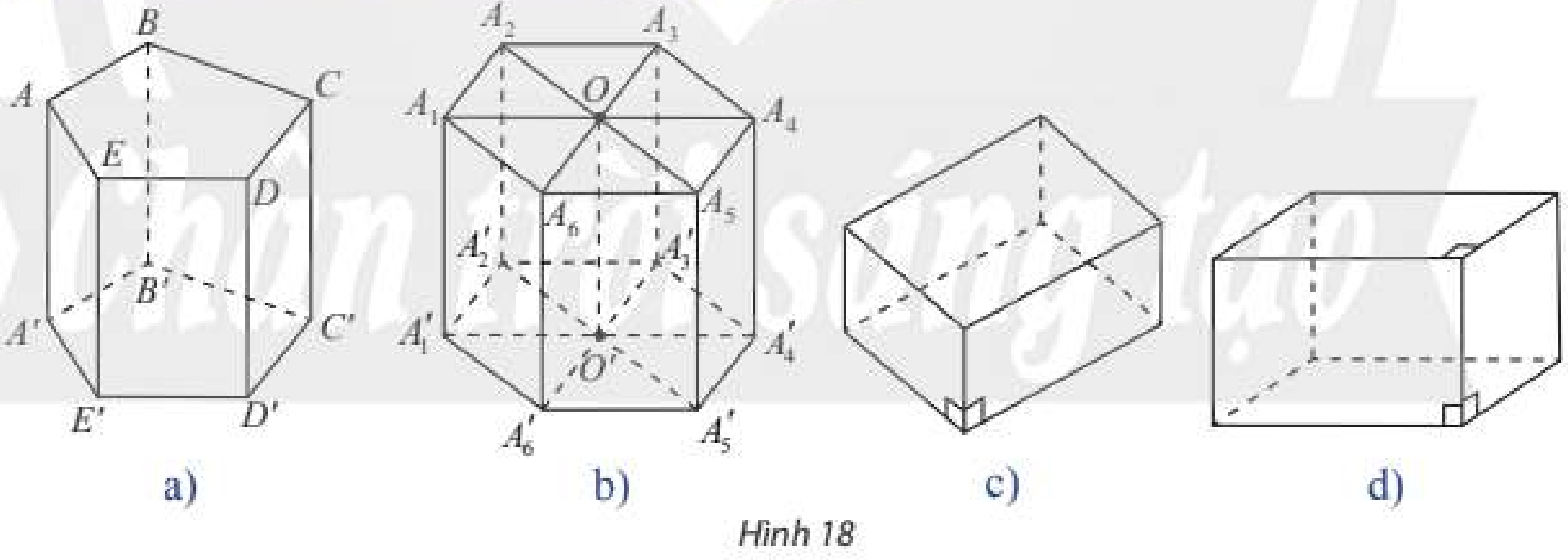
a) Cho hình lăng trụ (ABCDE.A'B'C'D'E') có cạnh bên (AA') vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 6

a) Cho hình lăng trụ \(ABCDE.A'B'C'D'E'\) có cạnh bên \(AA'\) vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?

b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b). Có nhận xét gì các mặt bên của hình lăng trụ này?

c) Một hình lăng trụ nếu có đây là hình bình hành và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18c) thì có bao nhiêu mặt là hình chữ nhật?

d) Một hình hộp nếu có đáy là hình chữ nhật và có cạnh bên vuông góc với mặt phẳng đáy (Hinh 18d) thì có bao nhiêu mặt là hình chữ nhật?

Phương pháp giải:

Quan sát hình ảnh và trả lời câu hỏi.

Lời giải chi tiết:

a) Các mặt bên của hình lăng trụ này là hình chữ nhật vuông góc với mặt phẳng đáy.

b) Các mặt bên của hình lăng trụ này là hình chữ nhật vuông góc với mặt phẳng đáy.

c) Hình lăng trụ đó có 4 mặt bên là hình chữ nhật.

d) Hình lăng trụ đó có cả 6 mặt là hình chữ nhật.

Thực hành 3

Cho hình lăng trụ lục giác đều \(ABCDEF.A'B'C'D'E'F'\) có cạnh bên bằng \(h\) và cạnh đáy bằng \(a\). Tính \(A'C\) và \(A'D\) theo \(a\) và \(h\).

Phương pháp giải:

Sử dụng phép chiếu vuông góc.

Lời giải chi tiết:

 

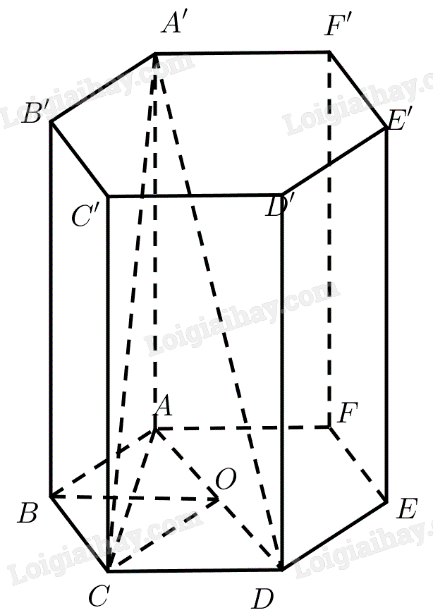
Tam giác \(ABC\) có:

\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}}  = a\sqrt 3 \)

\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AC\)

\( \Rightarrow \Delta AA'C\) vuông tại \(A\)

\( \Rightarrow A'C = \sqrt {AA{'^2} + A{C^2}}  = \sqrt {{h^2} + 3{{\rm{a}}^2}} \).

Gọi \(O\) là tâm lục giác đều \(ABC{\rm{DEF}}\).

\(\Delta OAB,\Delta OC{\rm{D}}\) đều \( \Rightarrow OA = O{\rm{D}} = AB = a \Rightarrow A{\rm{D}} = 2a\)

\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AD\)

\( \Rightarrow \Delta AA'D\) vuông tại \(A\)

\( \Rightarrow A'D = \sqrt {AA{'^2} + A{D^2}}  = \sqrt {{h^2} + 4{{\rm{a}}^2}} \).

Vận dụng 3

Một chiếc lồng đèn kéo quân có dạng hình lăng trụ lục giác đều với cạnh đáy bằng 10 cm và cạnh bên bằng 30 cm (Hình 20). Tính tổng diện tích các mặt bên của chiếc lồng đèn đó. 

Phương pháp giải:

Tính diện tích 1 mặt. Tổng diện tích các mặt bên bằng 6 lần diện tích 1 mặt.

Lời giải chi tiết:

Diện tích một mặt bên của lồng đèn là: \(10.30 = 300\left( {c{m^2}} \right)\)

Tổng diện tích các mặt bên của chiếc lồng đèn đó là: \(300.6 = 1800\left( {c{m^2}} \right)\)


Bình chọn:
3.7 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store