Bài 3. Tính chất của phép khai phương - Toán 9 Chân trờ..

Giải mục 3 trang 49, 50 SGK Toán 9 tập 1 - Chân trời sáng tạo

Thực hiện các phép tính có trên bảng trong Hình 2. b) Từ đó, có nhận xét gì về căn bậc hai của thương hai số dương?

Lựa chọn câu để xem lời giải nhanh hơn

HĐ4

Video hướng dẫn giải

Trả lời câu hỏi Hoạt động 4 trang 49 SGK Toán 9 Chân trời sáng tạo

a) Thực hiện các phép tính có trên bảng trong Hình 2.

b) Từ đó, có nhận xét gì về căn bậc hai của thương hai số dương?

Phương pháp giải:

Dựa vào \({\left( {\sqrt a } \right)^2} = {\left( { - \sqrt a } \right)^2} = a\) và \(\sqrt {{a^2}} = a\). ( a > 0)

Lời giải chi tiết:

(1) \(\sqrt {\frac{4}{9}} = \sqrt {{{\left( {\frac{2}{3}} \right)}^2}} = \frac{2}{3}\)

(2) \(\frac{{\sqrt 4 }}{{\sqrt 9 }} = \frac{{\sqrt {{2^2}} }}{{\sqrt {{3^2}} }} = \frac{2}{3}\)

(3) \(\sqrt {\frac{{16}}{{25}}} = \sqrt {{{\left( {\frac{4}{5}} \right)}^2}} = \frac{4}{5}\)

(4) \(\frac{{\sqrt {16} }}{{\sqrt {25} }} = \frac{{\sqrt {{4^2}} }}{{\sqrt {{5^2}} }} = \frac{4}{5}\)

b) Căn bậc hai của thương hai số dương bằng thương của căn bậc hai hai số dương.

TH6

Video hướng dẫn giải

Trả lời câu hỏi Thực hành 6 trang 50 SGK Toán 9 Chân trời sáng tạo

Tính

a) \(\sqrt {\frac{9}{{25}}} \)

b) \(\sqrt {1\frac{9}{{16}}} \)

c) \(\sqrt {150} :\sqrt 6 \)

d) \(\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} \)

Phương pháp giải:

Dựa vào tính chất: Với số thực a không âm và số thực b dương, ta có:

\(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\)

Lời giải chi tiết:

a) \(\sqrt {\frac{9}{{25}}} = \frac{{\sqrt 9 }}{{\sqrt {25} }} = \frac{3}{5}\)

b) \(\sqrt {1\frac{9}{{16}}} = \sqrt {\frac{{25}}{{16}}} = \frac{{\sqrt {25} }}{{\sqrt {16} }} = \frac{5}{4}\)

c) \(\sqrt {150} :\sqrt 6 = \sqrt {\frac{{150}}{6}} = \sqrt {25} = 5\)

d) \(\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} = \sqrt {\frac{3}{5}:\frac{5}{{12}}} = \sqrt {\frac{3}{5}.\frac{{12}}{5}} = \sqrt {\frac{{36}}{{25}}} = \frac{{\sqrt {36} }}{{\sqrt {25} }} = \frac{6}{5}\)

TH7

Video hướng dẫn giải

Trả lời câu hỏi Thực hành 7 trang 50 SGK Toán 9 Chân trời sáng tạo

Rút gọn các biểu thức sau:

a) \(\frac{{\sqrt {555} }}{{\sqrt {111} }}\)

b) \(\sqrt {\frac{{{a^2}}}{{4{b^4}}}} \) với \(a \ge 0;b \ne 0\)

c) \(\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }}\) với a > 1

Phương pháp giải:

Dựa vào tính chất: Với số thực a không âm và số thực b dương, ta có:

\(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\)

Lời giải chi tiết:

a) \(\frac{{\sqrt {555} }}{{\sqrt {111} }} = \sqrt {\frac{{555}}{{111}}} = \sqrt 5 \)

b) \(\sqrt {\frac{{{a^2}}}{{4{b^4}}}} = \frac{{\sqrt {{a^2}} }}{{\sqrt {4{b^4}} }} = \frac{a}{{2{b^2}}}\)

c) \(\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }} = \sqrt {\frac{{2{a^2}{{(1 - a)}^2}}}{{50}}} = \sqrt {\frac{{{a^2}{{(1 - a)}^2}}}{{25}}} = \frac{{\sqrt {{a^2}{{(1 - a)}^2}} }}{{\sqrt {25} }} = \frac{{a(a-1)}}{5}\)

VD2

Video hướng dẫn giải

Trả lời câu hỏi Vận dụng 2 trang 50 SGK Toán 9 Chân trời sáng tạo

Biết rằng hình tam giác và hình chữ nhật ở Hình 3 có diện tích bằng nhau. Tính chiều rộng x của hình chữ nhật.

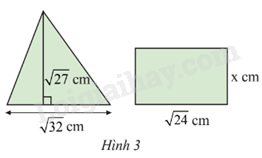
Phương pháp giải:

Dựa vào công thức diện tích tam giác S = \(\frac{1}{2}a.h\) (h: chiều cao,a: độ dài đáy) và diện tích hình chữ nhật S = a.b (a:chiều dài; b: chiều rộng).

Lời giải chi tiết:

Diện tích tam giác là: \(\frac{1}{2}.\sqrt {27} .\sqrt {32} = \frac{1}{2}.\sqrt {3.9} .\sqrt {16.2} = \frac{1}{2}.3\sqrt 3 .4\sqrt 2 = 6\sqrt 6 \) cm²

Suy ra diện tích hình chữ nhật là \(6\sqrt 6 \) cm²

Vậy x = \(\frac{{6\sqrt 6 }}{{\sqrt {24} }} = \frac{{6\sqrt 6 }}{{2\sqrt 6 }} = 3\)cm.

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 5 phiếu

Bài tiếp theo

Giải bài tập 1 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tính a) (sqrt {{{left( { - 10} right)}^2}} ) b) (sqrt {{{left( { - frac{2}{7}} right)}^2}} ) c) ({left( { - sqrt 2 } right)^2} - sqrt {25} ) d) ({left( { - sqrt {frac{2}{3}} } right)^2}.sqrt {0,09} )
Giải bài tập 2 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Rút gọn các biểu thức sau: a) (sqrt {{{left( {3 - sqrt {10} } right)}^2}} ) b) (2sqrt {{a^2}} + 4a) với a < 0 c) (sqrt {{a^2}} + sqrt {{{left( {3 - a} right)}^2}} ) với 0 < a < 3
Giải bài tập 3 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tính a) (sqrt {16.0,25} ) b) (sqrt {{2^4}.{{( - 7)}^2}} ) c) (sqrt {0,9} .sqrt {1000} ) d) (sqrt 2 .sqrt 5 .sqrt {40} )
Giải bài tập 4 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Rút gọn các biểu thức sau: a) (sqrt {{8^2}.5} ) b) (sqrt {81{a^2}} ) với a < 0 c) (sqrt {5a} .sqrt {45a} - 3a) với a ( ge ) 0
Giải bài tập 5 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tính a) (sqrt {frac{{0,49}}{{81}}} ) b) (sqrt {2frac{7}{9}} ) c) (sqrt {frac{1}{{16}}.frac{9}{{36}}} ) d) (left( { - sqrt {52} } right):sqrt {13} )
Giải bài tập 6 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Rút gọn các biểu thức sau: a) (frac{{sqrt 5 .sqrt 6 }}{{sqrt {10} }}) b) (frac{{sqrt {24{a^3}} }}{{sqrt {6a} }}) với a > 0 c) (sqrt {frac{{3{a^2}b}}{{27}}} ) với (a le 0;b ge 0)
Giải bài tập 7 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hình chữ nhật có chiều rộng a (cm), chiều dài b (cm) và diện tích S (cm2) a) Tìm S, biết a = (sqrt 8 ); b = (sqrt {32} ). b) Tìm b, biết S = (3sqrt 2 ); a = (2sqrt 3 )
Giải bài tập 8 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Từ một tấm thép hình vuông, người thợ cắt hai mảnh hình vuông có diện tích lần lượt là 24 cm2 và 40 cm2 như Hình 4. Tính diện tích phần còn lại của tấm thép.
Giải câu hỏi đố vui trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tìm chỗ sai trong phép chứng minh “voi con nặng bằng voi mẹ” sau đây: (begin{array}{l}{M^2} - 2Mm + {m^2} = {m^2} - 2mM + {M^2}\{(M - m)^2} = {(m - M)^2}\sqrt {{{(M - m)}^2}} = sqrt {{{(m - M)}^2}} \M - m = m - M\2M = 2m\M = m(!)end{array})
Giải mục 2 trang 47, 48, 49 SGK Toán 9 tập 1 - Chân trời sáng tạo
Thực hiện các phép tính cho trên bảng trong Hình 1. b) Từ đó, có nhận xét gì về căn bậc hai của tích hai số không âm?
Giải mục 1 trang 46, 47 SGK Toán 9 tập 1 - Chân trời sáng tạo
Hoàn thành bảng sau vào vở. Từ đó, nhận xét gì về căn bậc hai số học của bình phương của một số?
Lý thuyết Tính chất của phép khai phương Toán 9 Chân trời sáng tạo
1. Căn thức bậc hai của một bình phương Tính chất Với biểu thức A bất kì, ta có \(\sqrt {{A^2}} = \left| A \right|\), nghĩa là \(\sqrt {{A^2}} = A\) khi \(A \ge 0\); \(\sqrt {{A^2}} = - A\) khi \(A < 0\).