Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá Bài 3. Hình cầu - Toán 9 Cùng khám phá

Giải mục 2 trang 79, 80 SGK Toán 9 tập 2 - Cùng khám phá


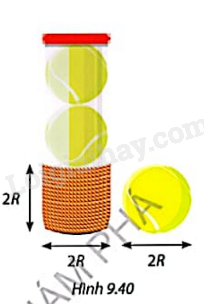
Bạn An dùng một sợi dây dù dài và mỏng cuốn quanh một quả bóng đến khi bọc kín quả bóng đó bằng các vòng cuốn sát nhau và không chồng lên nhau (Hình 9.39). Bạn An cắt sợi dây dù tại điểm kết thúc quá trình cuốn dây quanh quả bóng, rồi lấy đoạn dây này cuốn từng vòng sát nhau quanh hộp hình trụ đựng quả bóng đó (Hình 9.40). Bạn An thấy rằng đoạn dây cuốn quanh hộp đựng bóng tạo thành một hình trụ có đường kính và chiều cao cùng bằng đường kính quả bóng. a) So sánh diện tích bề mặt quả bóng v

Lựa chọn câu để xem lời giải nhanh hơn

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 79 SGK Toán 9 Cùng khám phá

Bạn An dùng một sợi dây dù dài và mỏng cuốn quanh một quả bóng đến khi bọc kín quả bóng đó bằng các vòng cuốn sát nhau và không chồng lên nhau (Hình 9.39).

Bạn An cắt sợi dây dù tại điểm kết thúc quá trình cuốn dây quanh quả bóng, rồi lấy đoạn dây này cuốn từng vòng sát nhau quanh hộp hình trụ đựng quả bóng đó (Hình 9.40). Bạn An thấy rằng đoạn dây cuốn quanh hộp đựng bóng tạo thành một hình trụ có đường kính và chiều cao cùng bằng đường kính quả bóng.

a) So sánh diện tích bề mặt quả bóng với phần diện tích của hộp đựng bị quấn bởi sợi dây dù.

b) Gọi R là bán kính của quả bóng. Viết công thức tính diện tích xung quanh của hình trụ do đoạn dây cuốn quanh hộp đựng bóng tạo thành theo R, từ đó suy ra diện tích bề mặt của quả bóng.

Phương pháp giải:

Nhìn hình và nhận xét.

Lời giải chi tiết:

a) Diện tích bề mặt quả bóng bằng với diện tích xung quanh của hộp đựng.

b) Diện tích xung quanh của hộp đựng là:

\(S = 2\pi .R.2R = 4\pi {R^2}\)

Diện tích bề mặt quả bóng là:

\(S = 4\pi {R^2}\).

LT2

Trả lời câu hỏi Luyện tập 2 trang 80 SGK Toán 9 Cùng khám phá

Một mặt cầu có diện tích là 36 cm2. Hỏi đường kính của mặt cầu này là bao nhiêu centimet (làm tròn kết quả đến hàng phần trăm)?

Phương pháp giải:

Diện tích mặt cầu là: \(S = 4\pi {R^2} = \pi {d^2}\) (R là bán kính và d là đường kính của mặt cầu)

Lời giải chi tiết:

Ta có \(S = \pi {d^2} = 36\)

Suy ra \(d = \sqrt {\frac{{36}}{\pi }} \approx 3,39\)cm.

VD2

Trả lời câu hỏi Vận dụng 2 trang 80 SGK Toán 9 Cùng khám phá

Đại dương bao phủ khoảng 71% bề mặt Trái Đất. Hãy ước tính diện tích của đại dương theo kilomet vuông, biết bán kính Trái Đất khoảng 6371 km (làm tròn kết quả đến hàng triệu).

Phương pháp giải:

Diện tích mặt cầu là: \(S = 4\pi {R^2} = \pi {d^2}\) (R là bán kính và d là đường kính của mặt cầu)

Lời giải chi tiết:

Diện tích Trái Đất là:

\(S = 4\pi {R^2} = 4\pi .{\left( {6371} \right)^2} = 510\)(trệu km2)

Đại dương bao phủ khoảng 71% bề mặt Trái Đất nên diện tích đại dương khoảng: 510.71% = 362 triệu km2.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải mục 3 trang 81, 82 SGK Toán 9 tập 2 - Cùng khám phá

    Bạn Mai thả từ từ một quả cầu bán kính R vào một chiếc cốc thuỷ tinh hình trụ chứa sẵn nước đến \(\frac{1}{3}\) chiều cao cốc (Hình 9.41a) thì thấy nước dâng lên vừa miệng cốc (Hình 9.41b). Dựa vào kết quả thí nghiệm của bạn Mai, viết công thức tính: a) Thể tích của chiếc cốc hình trụ theo R b) Thể tích của quả cầu.

  • Giải mục 4 trang 82 SGK Toán 9 tập 2 - Cùng khám phá

    Ta có thể làm một quả cầu để trang trí theo các bước sau: Bước 1: Cắt 16 miếng bìa hình tròn có bán kính 4 cm và gấp đôi theo nếp gấp là đường kính bất kì (Hình 9.44a) Bước 2: Dùng keo dán hoặc băng dính hai mặt để dán các miếng bìa trên với nhau tạo thành quả cầu (Hình 9.44b).

  • Giải bài tập 9.10 trang 83 SGK Toán 9 tập 2 - Cùng khám phá

    Tìm các số và đơn vị thích hợp ở ô ? để hoàn thành Bảng 9.3.

  • Giải bài tập 9.11 trang 83 SGK Toán 9 tập 2 - Cùng khám phá

    Một quả dưa hấu có dạng hình cầu với bán kính 12 cm và vỏ dày 1 cm (Hình 9.46). Tính diện tích bề mặt quả dưa hấu và thể tích vỏ dưa.

  • Giải bài tập 9.12 trang 83 SGK Toán 9 tập 2 - Cùng khám phá

    Tính khối lượng thép cần dùng để sản xuất 1000 chiếc đinh tán có thân hình trụ và đầu là nửa hình cầu với kích thước như Hình 9.47, biết khối lượng riêng của thép là 7850 kg/m3.

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua