Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số - ..

Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Chân trời sáng tạo


Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn

Tổng hợp đề thi giữa kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Lựa chọn câu để xem lời giải nhanh hơn

KP2

Trả lời câu hỏi Khám phá 2 trang 16 SGK Toán 12 Chân trời sáng tạo

Hình 3 cho ta đồ thị của ba hàm số

\(f(x) = \frac{1}{2}{x^2}\); \(g(x) = \left\{ \begin{array}{l}\frac{1}{2}{x^2}\;\;\;\;\;\;\;\;\;\;\;neu\;x \le 2\;\\ - 4x + 10\;\;\;\;neu\;x \ge 2\end{array} \right.\) và \(h(x) = 3 - \frac{1}{2}{x^2}\) trên đoạn [-1;3]

a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?

b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?

Phương pháp giải:

Quan sát đồ thị và chỉ ra điểm cực đại và giá trị lớn nhất của 3 hàm số.

Lời giải chi tiết:

a) \(h(x)\)đạt giá trị cực đại tại x = 0 và \(\mathop {\max h(x)}\limits_{[ - 1;3]}  = h(0) = 3\)

b) \(\mathop {\max f(x)}\limits_{[ - 1;3]}  = f(3) = \frac{9}{2}\) và \(\mathop {\max g(x)}\limits_{[ - 1;3]}  = g(2) = 2\)

TH2

Trả lời câu hỏi Thực hành 2 trang 18 SGK Toán 12 Chân trời sáng tạo

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]

Phương pháp giải:

Tìm đạo hàm g’(x), lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Lời giải chi tiết:

Xét \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]

\(g'(x) = 1 - \frac{8}{{{x^3}}} = 0 \Leftrightarrow x = 2\)

Bảng biến thiên:

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[1;4]} g(x) = g(2) = 3\) và \(\mathop {\max }\limits_{[1;4]} g(x) = g(1) = 5\)

TH3

Trả lời câu hỏi Thực hành 3 trang 18 SGK Toán 12 Chân trời sáng tạo

Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?

Phương pháp giải:

Tìm hệ thức liên hệ giữa các cạnh, từ đó suy ra hàm số của diện tích tam giác vuông. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất của hàm số

Lời giải chi tiết:

Đặt một cạnh góc vuông là x (x > 0) thì cạnh còn lại là \(\sqrt {25 - {x^2}} \)

Diện tích tam giác vuông là: \(f(x) = \frac{{1}}{2} x\sqrt {25 - {x^2}} \)

Tập xác định: \(D = (0; 5 )\)

\(f'(x) = \frac{{1}}{2}\sqrt {25 - {x^2}}  - \frac{{1}}{2}. \frac{{{x^2}}}{{\sqrt {25 - {x^2}} }}\)

Tập xác định mới: \({D_1} = (0; 5 )\)

\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\sqrt {2} }}{2}\\x =  - \frac{{5\sqrt {2} }}{2}(loại)\end{array} \right.\)

Bảng biến thiên:

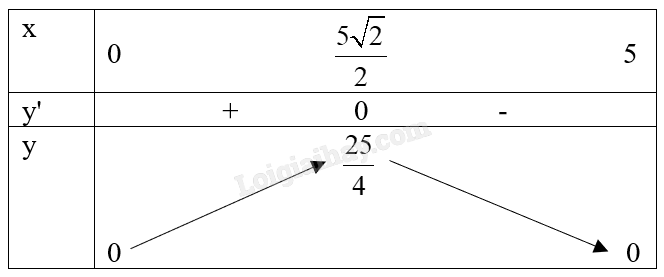
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D f(x) = f(\frac{{5\sqrt {2} }}{2}) = \frac{25}{4}\).

Vậy diện tích lớn nhất của tam giác là \(\frac{25}{4}\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store