Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: a) (y = {x^3} - 12x + 1) trên đoạn [-1;3] b) (y = - {x^3} + 24{x^2} - 180x + 400) trên đoạn [3;11] c) (y = frac{{2x + 1}}{{x - 2}}) trên đoạn [3;7] d) (y = sin 2x) trên đoạn ([0;frac{{7pi }}{{12}}])

Đề bài

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) $y = {x^3} - 12x + 1$ trên đoạn [-1;3]
b) $y = - {x^3} + 24{x^2} - 180x + 400$ trên đoạn [3;11]
c) $y = \frac{{2x + 1}}{{x - 2}}$ trên đoạn [3;7]
d) $y = \sin 2x$ trên đoạn $[0;\frac{{7\pi }}{{12}}]$

Phương pháp giải - Xem chi tiết

Tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Lời giải chi tiết

a) Xét $y = {x^3} - 12x + 1$ trên đoạn [-1;3]

$y' = 3{x^2} - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2(loai)\end{array} \right.$

Bảng biến thiên:

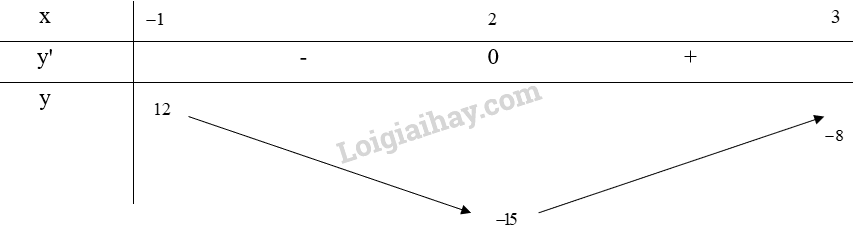
Từ bảng biến thiên, ta thấy $\mathop {\max }\limits_{[ - 1;3]} y = y( - 1) = 12$ và $\mathop {\min }\limits_{[ - 1;3]} y = y(2) = - 15$

b) Xét $y = - {x^3} + 24{x^2} - 180x + 400$ trên đoạn [3;11]

$y' = - 3{x^2} + 48x - 180 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = 6\end{array} \right.$

Bảng biến thiên:

Từ bảng biến thiên, ta thấy $\mathop {\max }\limits_{[3;11]} y = y(3) = 49$ và $\mathop {\min }\limits_{[3;11]} y = y(6) = - 32$

c) Xét $y = \frac{{2x + 1}}{{x - 2}}$ trên đoạn [3;7]

$y' = \frac{{ - 5}}{{{{(x - 2)}^2}}} < 0\forall x \in [3;7]$

Bảng biến thiên:

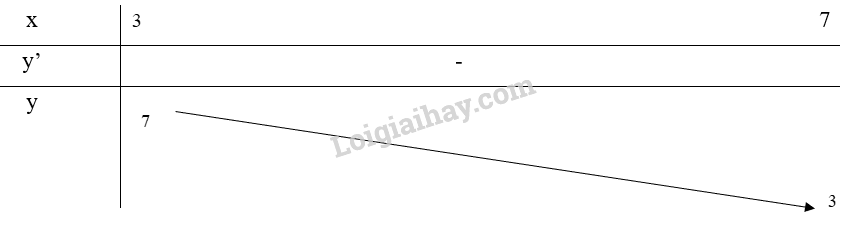
Từ bảng biến thiên, ta thấy $\mathop {\max }\limits_{[3;7]} y = y(3) = 7$ và $\mathop {\min }\limits_{[3;7]} y = y(7) = 3$

d) Xét $y = \sin 2x$ trên đoạn $[0;\frac{{7\pi }}{{12}}]$

$y' = 2\cos 2x = 0 \Leftrightarrow 2x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{4} + \frac{{k\pi }}{2}(k \in \mathbb{Z})$

Ta có: $x \in [0;\frac{{7\pi }}{{12}}] \Rightarrow k = 0 \Rightarrow x = \frac{\pi }{4}$

Bảng biến thiên:

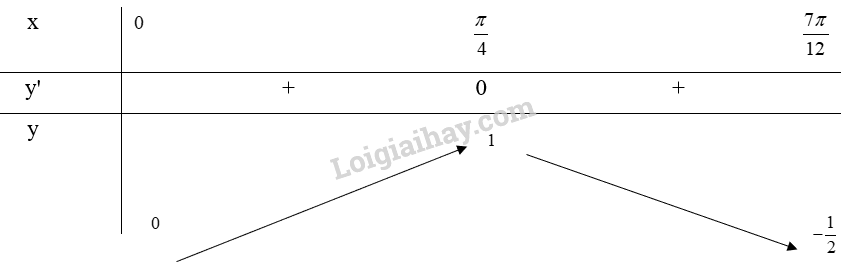
Từ bảng biến thiên, ta thấy $\mathop {\max }\limits_{[0;\frac{{7\pi }}{{12}}]} y = y(\frac{\pi }{4}) = 1$ và $\mathop {\min }\limits_{[0;\frac{{7\pi }}{{12}}]} y = y(\frac{{7\pi }}{{12}}) = - \frac{1}{2}$

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 7 phiếu

Bài tiếp theo

Giải bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị nhỏ nhất của các hàm số sau: a) (y = {x^3} - 3x - 4) trên nửa khoảng [-3;2) b) (y = frac{{3{x^2} - 4x}}{{{x^2} - 1}}) trên khoảng (( - 1; + infty ))
Giải bài tập 4 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khi làm nhà kho, bác An muốn cửa sổ có dạng hình chữ nhật với chu vi bằng 4m (Hình 6). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)?
Giải bài tập 5 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 2\sqrt {1 - {x^2}} + {x^2}$
Giải bài tập 6 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khối lượng $q$ (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán $p$ (nghìn đồng/kg) theo công thức $p = 15 - \frac{1}{2}q$ . Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức $R = pq$ . a) Viết công thức biểu diễn $R$ theo $p$ . b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.
Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Hộp sữa $1l$ được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.
Giải bài tập 1 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5
Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn
Giải mục 1 trang 14, 15, 16 SGK Toán 12 tập 1 - Chân trời sáng tạo
Định nghĩa
Lý thuyết Giá trị lớn nhất, giá trị nhỏ nhất của hàm số Toán 12 Chân trời sáng tạo
1. Định nghĩa Khái niệm GTLN, GTNN của hàm số

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.