Giải bài tập 5 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2\sqrt {1 - {x^2}} + {x^2}\)

Đề bài

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2\sqrt {1 - {x^2}} + {x^2}\)

Phương pháp giải - Xem chi tiết

tìm tập xác định, tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất

Lời giải chi tiết

Tập xác định: \(D = [ - 1;1]\)

\(y' = \frac{{ - 2x}}{{\sqrt {1 - {x^2}} }} + 2x = 0 \Leftrightarrow x = 0\)

Tập xác định mới: \({D_1} = ( - 1;1)\)

Bảng biến thiên:

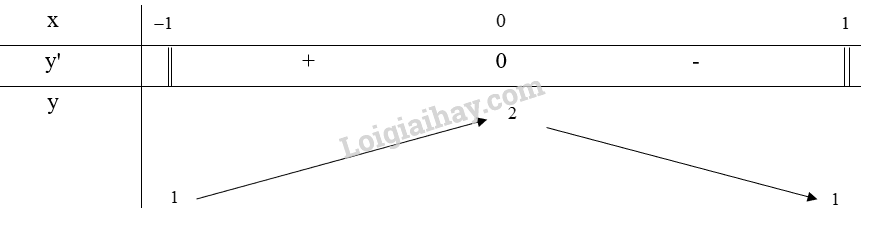
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D y = y(0) = 2\) và \(\mathop {\min }\limits_D y = y( - 1) = y(1) = 1\)

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 6 phiếu

Bài tiếp theo

Giải bài tập 6 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khối lượng \(q\) (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán \(p\) (nghìn đồng/kg) theo công thức \(p = 15 - \frac{1}{2}q\). Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức \(R = pq\). a) Viết công thức biểu diễn \(R\) theo \(p\). b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.
Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Hộp sữa \(1l\) được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.
Giải bài tập 4 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khi làm nhà kho, bác An muốn cửa sổ có dạng hình chữ nhật với chu vi bằng 4m (Hình 6). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)?
Giải bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị nhỏ nhất của các hàm số sau: a) (y = {x^3} - 3x - 4) trên nửa khoảng [-3;2) b) (y = frac{{3{x^2} - 4x}}{{{x^2} - 1}}) trên khoảng (( - 1; + infty ))
Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: a) (y = {x^3} - 12x + 1) trên đoạn [-1;3] b) (y = - {x^3} + 24{x^2} - 180x + 400) trên đoạn [3;11] c) (y = frac{{2x + 1}}{{x - 2}}) trên đoạn [3;7] d) (y = sin 2x) trên đoạn ([0;frac{{7pi }}{{12}}])
Giải bài tập 1 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5
Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn
Giải mục 1 trang 14, 15, 16 SGK Toán 12 tập 1 - Chân trời sáng tạo
Định nghĩa
Lý thuyết Giá trị lớn nhất, giá trị nhỏ nhất của hàm số Toán 12 Chân trời sáng tạo
1. Định nghĩa Khái niệm GTLN, GTNN của hàm số