 Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều
Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều
 Bài 2. Nguyên hàm của một số hàm số sơ cấp - Toán 12 Cá..
Bài 2. Nguyên hàm của một số hàm số sơ cấp - Toán 12 Cá..
Giải câu hỏi mở đầu trang 9 SGK Toán 12 tập 2 - Cánh diều
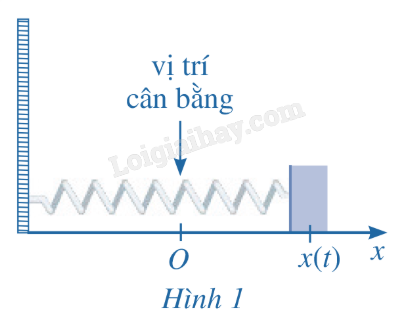
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát như Hình 1, có vận tốc tức thời cho bởi v(t) = 4cost, trong đó t tính bằng giây và v(t) tính bằng centimét/giây. Tại thời điểm t = 0, con lắc đó ở vị trí cân bằng. Phương trình chuyển động của con lắc đó được xác định bằng cách nào?
Đề bài
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát như Hình 1, có vận tốc tức thời cho bởi v(t) = 4cost, trong đó t tính bằng giây và v(t) tính bằng centimét/giây. Tại thời điểm t = 0, con lắc đó ở vị trí cân bằng. Phương trình chuyển động của con lắc đó được xác định bằng cách nào?
Phương pháp giải - Xem chi tiết
Tìm \(s(t) = \int {v(t)dt} \).
Lời giải chi tiết
Giả sử con lắc chuyển động theo phương trình: s = s(t).
Suy ra s’(t) = v(t), do đó s(t) là một nguyên hàm của v(t). Ta có:
\(\int {v(t)dt} = \int {4\cos tdt} = 4\int {\cos tdt} = 4\sin t + C\).
Suy ra s(t) = 4sint + C.
Tại thời điểm t = 0, ta có s(0) = 0, tức là 4sin0 + C = 0, suy ra C = 0.
Vậy phương trình chuyển động của con lắc là: s(t) = 4sint + C.
Các bài khác cùng chuyên mục












Danh sách bình luận