 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài tập cuối chương 4 - Toán 12 Cùng khám phá
Bài tập cuối chương 4 - Toán 12 Cùng khám phá
Giải bài tập 4.41 trang 38 SGK Toán 12 tập 2 - Cùng khám phá
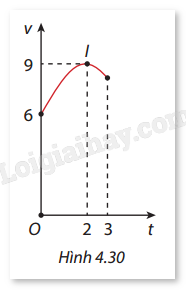
Một vật chuyển động trong 3 giờ với vận tốc \(v\) (km/h) phụ thuộc vào thời gian \(t\) (h) có đồ thị là một phần của đường parabol có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung như Hình 4.30. Tính quãng đường mà vật di chuyển được trong 3 giờ đó. A. \(25,25{\mkern 1mu} {\rm{km}}\) B. \(24,25{\mkern 1mu} {\rm{km}}\) C. \(24,75{\mkern 1mu} {\rm{km}}\) D. \(26,75{\mkern 1mu} {\rm{km}}\)
Đề bài
Một vật chuyển động trong 3 giờ với vận tốc \(v\) (km/h) phụ thuộc vào thời gian \(t\) (h) có đồ thị là một phần của đường parabol có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung như Hình 4.30. Tính quãng đường mà vật di chuyển được trong 3 giờ đó.
A. \(25,25{\mkern 1mu} {\rm{km}}\)
B. \(24,25{\mkern 1mu} {\rm{km}}\)
C. \(24,75{\mkern 1mu} {\rm{km}}\)
D. \(26,75{\mkern 1mu} {\rm{km}}\)
Phương pháp giải - Xem chi tiết
- Quãng đường mà vật di chuyển được tính bằng tích phân của vận tốc theo thời gian:
\(S = \int_0^3 v (t){\mkern 1mu} dt\)
- Hàm \(v(t)\) là một phần của parabol, có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung. Từ đó, ta cần tìm phương trình của \(v(t)\) và tính tích phân trên đoạn từ \(0\) đến \(3\).
Lời giải chi tiết
Ta biết rằng đồ thị \(v(t)\) có dạng một parabol với đỉnh \(I(2;9)\), vậy phương trình của parabol có dạng:
\(v(t) = a{(t - 2)^2} + 9\)
Dựa vào điểm \((0,6)\) trên đồ thị (vận tốc tại thời điểm \(t = 0\)), ta thay vào phương trình để tìm \(a\):
\(6 = a{(0 - 2)^2} + 9\)
\(6 = 4a + 9 \Rightarrow 4a = - 3 \Rightarrow a = - \frac{3}{4}\)
Vậy phương trình của vận tốc là:
\(v(t) = - \frac{3}{4}{(t - 2)^2} + 9\)
Bây giờ, ta tính quãng đường \(S\) bằng cách lấy tích phân:
\(S = \int_0^3 {\left( { - \frac{3}{4}{{(t - 2)}^2} + 9} \right)} dt = \int_0^3 - \frac{3}{4}{(t - 2)^2}{\mkern 1mu} dt + \int_0^3 9 {\mkern 1mu} dt\)
Tính tích phân của \(9\):
\(\int_0^3 9 {\mkern 1mu} dt = 9t|_0^3 = 9(3 - 0) = 27\)
Tính tích phân của \( - \frac{3}{4}{(t - 2)^2}\): Sử dụng biến đổi \(u = t - 2\), tích phân trở thành:
\(\int_0^3 - \frac{3}{4}{(t - 2)^2}{\mkern 1mu} dt = \int_{ - 2}^1 - \frac{3}{4}{u^2}{\mkern 1mu} du\)
Tính tích phân của \({u^2}\):
\(\int_{ - 2}^1 - \frac{3}{4}{u^2}{\mkern 1mu} du = - \frac{3}{4} \cdot \frac{{{u^3}}}{3}|_{ - 2}^1 = - \frac{1}{4}\left( {{1^3} - {{( - 2)}^3}} \right) = - \frac{1}{4}(1 + 8) = - \frac{9}{4}\)
Vậy quãng đường \(S\) là:
\(S = 27 - \frac{9}{4} = \frac{{108}}{4} - \frac{9}{4} = \frac{{99}}{4} = 24,75{\mkern 1mu} {\rm{km}}\)
Chọn C.
- Giải bài tập 4.42 trang 39 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 4.43 trang 39 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 4.40 trang 38 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 4.39 trang 38 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 4.38 trang 38 SGK Toán 12 tập 2 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận