 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài tập cuối chương 1 - Toán 12 Chân trời sáng tạo
Bài tập cuối chương 1 - Toán 12 Chân trời sáng tạo
Giải bài tập 14 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo
Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b
Đề bài
Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: \(r = \frac{{5(12 - h)}}{{12}}\).
b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: \(V(h) = \frac{{25\pi h{{(12 - h)}^2}}}{{144}}\).
c) Tìm h để khối trụ có thể tích lớn nhất.
Phương pháp giải - Xem chi tiết
a) Từ hình vẽ, tìm mối liên hệ giữa r và h thông qua các công thức tính diện tích, thể tích,….
b) Thể tích khối trụ là \(V = \pi {r^2}h\).
c) Lập bảng biến thiên và quan sát.
Lời giải chi tiết
a) Xét nửa tam giác lớn Hình 4b. Diện tích hình chữ nhật bằng diện tích tam giác lớn trừ diện tích hai tam giác nhỏ.
Ta có: \(rh = \frac{1}{2}.12.5 - \frac{1}{2}.h(5 - r) - \frac{1}{2}(12 - h).r = \frac{{60 - 5h + rh - 12r + rh}}{2}\)
\( \Leftrightarrow 2rh = 60 - 5h + 2rh - 12r \Leftrightarrow 12r = 60 - 5h \Leftrightarrow r = \frac{{5(12 - h)}}{{12}}\).
b) Thể tích khối trụ là: \(V(h) = \pi {r^2}h = \pi .\frac{{{5^2}{{(12 - h)}^2}}}{{{{12}^2}}}h = \frac{{25\pi h{{(12 - h)}^2}}}{{144}}\).
c) Thể tích khối trụ lớn nhất khi V(h) đạt giá trị lớn nhất. Ta tìm max của hàm V(h) bằng cách tìm đạo hàm V'(h) và lập bảng biến thiên.
\(V'(h) = \frac{{75\pi {h^2} - 1200\pi h + 3600\pi }}{{144}} = 0 \Leftrightarrow \left[ \begin{array}{l}h = 4\\h = 12\end{array} \right.\)
Bảng biến thiên:
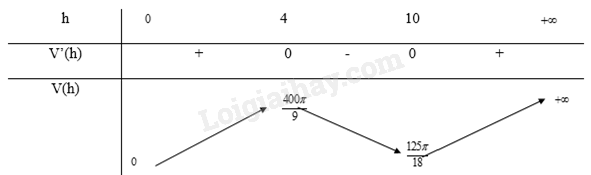
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{(0; + \infty )} V(h) = V(4) = \frac{{400\pi }}{9}\).
Vậy để khối trụ có thể tích lớn nhất thì h = 4cm.
- Giải bài tập 15 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 16 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 13 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 12 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 11 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận