Giải bài 6 trang 81 vở thực hành Toán 9

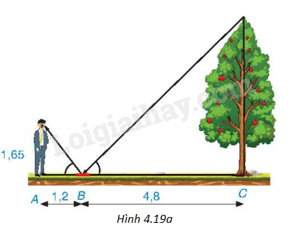
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây mọc thẳng đứng, có gốc ở tại điểm C cách B là 4,8m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65m. Tính chiều cao của cây (H.4.19a).

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây mọc thẳng đứng, có gốc ở tại điểm C cách B là 4,8m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65m. Tính chiều cao của cây (H.4.19a).

Phương pháp giải - Xem chi tiết

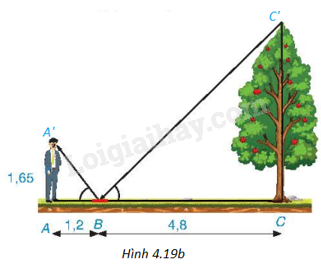
+ Gọi A’ là điểm tại mắt người đứng, C’ là đỉnh ngọn cây (H.4.19b) thì theo quang học, ta có \(\widehat {ABA'} = \widehat {CBC'}\). Khi đó,

+ Vì \(\tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{{1,65}}{{1,2}}\), \(\tan \widehat {CBC'} = \frac{{CC'}}{{CB}}\) nên \(\frac{{CC'}}{{BC}} = \frac{{1,65}}{{1,2}}\), từ đó tính được CC’.

Lời giải chi tiết

Gọi A’ là điểm tại mắt người đứng, C’ là đỉnh ngọn cây (H.4.19b) thì theo quang học, ta có \(\widehat {ABA'} = \widehat {CBC'}\).

Trong tam giác ABA’, ta có \(\tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{{1,65}}{{1,2}}\);

Trong tam giác CBC’, ta có \(\tan \widehat {CBC'} = \frac{{CC'}}{{CB}}\).

Vì \(\widehat{ABA'} = \widehat {CBC'}\) nên \(\tan \widehat{ABA'} = \tan {CBC'}\) hay \(\frac{{CC'}}{{BC}} = \frac{{1,65}}{{1,2}}\)

Suy ra \(CC' = \frac{{1,65BC}}{{1,2}} = \frac{{1,65.4,8}}{{1,2}} = 6,6\left( m \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 82 vở thực hành Toán 9
Để đo chiều rộng của một khúc sông, có hai người đã làm như sau: Hai người đứng ở hai vị trí A, B trên hai bên bờ sông, nhìn thấy đỉnh một tỏa tháp phía xa dưới góc ({40^o}) và góc ({55^o}) (H.4.20). Biết tòa tháp cao 300m, từ đó tính được khoảng cách AB. Em hãy cho biết, họ tính AB bằng bao nhiêu mét.
Giải bài 8 trang 83 vở thực hành Toán 9
Một người đứng cách gốc cây 20m nhìn thấy ngọn cây với góc ({36^o}) so với phương nằm ngang. Biết mắt người ấy cách mặt đất 1,7m và cây mọc thẳng đứng (H.4.21a). Tính chiều cao của cây (làm tròn đến chữ số thập phân thứ nhất).
Giải bài 9 trang 84 vở thực hành Toán 9
Cho tam giác ABC vuông tại A, (BC = 10,AB = 6). a) Giải tam giác ABC. b) Từ B kẻ đường thẳng vuông góc với BC, cắt AC tại D. Tính BD, CD, AD và góc ABD. (Góc làm tròn đến độ, cạnh làm tròn đến chữ số thập phân thứ nhất).
Giải bài 5 trang 80 vở thực hành Toán 9
Cho hình thang ABCD (AD//BC) có (AD = 16cm,BC = 4cm) và (widehat A = widehat B = widehat {ACD} = {90^o}). a) Kẻ đường cao CE của tam giác ACD. Chứng minh (widehat {ADC} = widehat {ACE}). Tính sin của các góc (widehat {ADC},widehat {ACE}) và suy ra (A{C^2} = AD.AE). Từ đó tính AC. b) Tính góc D của hình thang.
Giải bài 4 trang 80 vở thực hành Toán 9
Tính các góc của hình thoi có hai đường chéo dài (2sqrt 3 ) và 2.
Giải bài 3 trang 79 vở thực hành Toán 9
Tính góc nghiêng (alpha ) và chiều rộng AB của mái nhà kho trong Hình 4.16 (góc làm tròn đến độ, độ dài làm tròn đến dm).
Giải bài 2 trang 78 vở thực hành Toán 9
Tính góc nghiêng (alpha ) của thùng xe chở rác trong Hình 4.15a.
Giải bài 1 trang 78 vở thực hành Toán 9
Giải tam giác ABC vuông tại A có (BC = a,AC = b,AB = c,) trong các trường hợp (góc làm tròn đến độ, cạnh làm tròn đến chữ số hàng đơn vị): a) (a = 21,b = 18); b) (b = 10,widehat C = {30^o}); c) (c = 5;b = 3).
Giải câu hỏi trắc nghiệm trang 77, 78 vở thực hành Toán 9
Cho tam giác PQR như Hình 4.12. Khi đó ta có: A. (PQ = PR.sin P). B. (PQ = PR.cos R). C. (QR = PR.cos P). D. (QR = PR.cos R).