Bài 23.7, 23.8, 23.9, 23.10 trang 56 SBT Vật lí 10
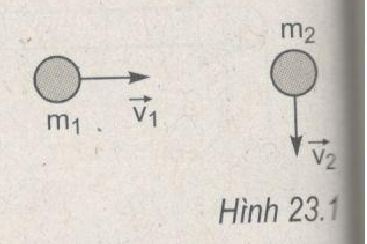
Giải bài 23.7, 23.8, 23.9, 23.10 trang 56 sách bài tập vật lý 10. Hai viên bi có khối lượng 2 g và 3 g, chuyển động trên mặt phẳng ngang không ma sát với vận tốc 6 m/s (viên bi 2 g) và 4 m/s (viên bi 3 g) theo hai phương vuông góc (Hình 23.1). Xác định tổng động lượng của hệ hai viên bi.
23.7.
Hai viên bi có khối lượng 2 g và 3 g, chuyển động trên mặt phẳng ngang không ma sát với vận tốc 6 m/s (viên bi 2 g) và 4 m/s (viên bi 3 g) theo hai phương vuông góc (Hình 23.1). Xác định tổng động lượng của hệ hai viên bi.
Phương pháp giải:
Áp dụng công thức \(\overrightarrow p = m\overrightarrow v \)
Định lí Pytago \({p^2} = p_1^2 + p_2^2\)
Lời giải chi tiết:
Tổng động lượng của hệ hai viên bi :
\(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
Trong đó \(\overrightarrow {{p_1}} = {m_1}\overrightarrow {{v_1}} \) và \(\overrightarrow {{p_2}} = {m_2}\overrightarrow {{v_2}} \)
với:
\(p_1=m_1v_1= 2.10^{-3}.6 \\= 1,2.10^{-2}kg.m/s\)
\(p_2=m_2v_2=3.10^{-3}.4 \\= 1.2.10^{-2}kg.m/s\)
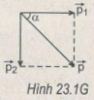
Vì \(\overrightarrow {{p_1}} \bot \overrightarrow {{p_2}} \) (H.23.1G)
Và p1 = p2 = 1,2.10-2 kg.m/s,
Nên vectơ \(\overrightarrow p \) trùng với đường chéo của hình vuông có các cạnh p1 = p2.
Từ đó suy ra : \(\overrightarrow p \) hợp \(\overrightarrow p_1 \) (hoặc \(\overrightarrow p_2 \) ) một góc α = 450 và có độ lớn :
p = p1.\(\sqrt 2\) ≈ 1,2.10-2.1,4 ≈ 1,7.10-2 kg.m/s
23.8.
Một người khối lượng 50 kg đứng ở phía đuôi của một chiếc thuyền khối lượng 450 kg đang đỗ trên mặt hồ phẳng lặng. Người này bắt đầu đi về phía đầu thuyền. Xác định vận tốc chuyển động của thuyền trong hai trường hợp :
a) vận tốc của người đối với mặt hồ là 0,5 m/s.
b) vận tốc của người đối với thuyền là 0,5 m/s.
Phương pháp giải:
Áp dụng định luật bảo toàn động lượng \(\overrightarrow {{p_1}} + \overrightarrow {{p_2}} = \overrightarrow {p{'_1}} + \overrightarrow {p{'_2}} \)
Lời giải chi tiết:
Chọn chiều chuyển động của người là chiều dương. Hệ vật gồm thuyền và người. Do không có ma sát và tổng các ngoại lực tác dụng lên hệ vật (trọng lực và phản lực pháp tuyến) cân bằng nhau theo phương đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn.
Lúc đầu, hệ vật đứng yên đối với mặt hồ phẳng lặng (V0 = 0), nên tổng động lượng của nó có trị đại số bằng : p0 = (M + m)V0 = 0.
a. Khi người chạy với vận tốc v = 0,5 m/s đối với mặt hồ, thì tổng động lượng của hệ vật có trị đại số bằng : p = M.v + m.v.
Áp dụng định luật bảo toàn động lượng : p = p0 => MV + mv = 0
suy ra vận tốc của thuyền : \(V = - \displaystyle{{mv} \over M} = - {{50.0,5} \over {450}} \approx - 0,056(m/s)\)
Dấu trừ chứng tỏ vận tốc của thuyền ngược hướng với vận tốc của người
b. Khi người chạy với vận tốc v = 0,5 m/s đối với thuyền, thì tổng động lượng của hệ vật bằng :
p = MV + m(v + V).
Áp dụng định luật bảo toàn động lượng :
p = p0 => MV + m(v + V) =0
suy ra vận tốc của thuyền : \(V = - \displaystyle{{mv} \over {M + m}} = - {{50.0,5} \over {450 + 50}} \\= - 0,05(m/s)\)
Dấu trừ chứng tỏ vận tốc của thuyền ngược hướng với vận tốc của người.
23.9.
Một xe nhỏ chở cát khối lượng 98 kg đang chạy với vận tốc 1 m/s trên mặt đường phẳng ngang không ma sát. Một vật nhỏ khối lượng 2 kg bay theo phương ngang với vận tốc 6 m/s (đối với mặt đường) đến xuyên vào trong cát. Xác định vận tốc của xe cát sau khi vật nhỏ xuyên vào nó trong hai trường hợp :
a) Vật bay đến ngược chiều chuyển động của xe cát.
b) Vật bay đến cùng chiều chuyển động của xe cát.
Phương pháp giải:
Áp dụng định luật bảo toàn động lượng \(\overrightarrow {{p_1}} + \overrightarrow {{p_2}} = \overrightarrow {p{'_1}} + \overrightarrow {p{'_2}} \)
Lời giải chi tiết:
Chọn chiều chuyển động ban đầu của xe cát là chiều dương. Hệ vật gồm xe cát và vật nhỏ chuyển động theo cùng phương ngang, nên có thể biểu diễn tổng động lượng của hệ vật này dưới dạng tổng đại số.
Trước khi vật xuyên vào xe cát: \(p_0= MV_0+ mv_0\).
Sau khi vật xuyên vào xe cát: \(p = (M + m)V\).
Áp dụng định luật bảo toàn động lượng, ta có :
p = p0 => (M + m)V = MV0 + mv0
Suy ra : \(V = \displaystyle{{M{V_0} + m{v_0}} \over {M + m}}\)
a. Khi vật bay đến ngược chiều chuyển động của xe cát, thì v0 = -6 m/s, nên ta có :
\(V = \displaystyle{{98.1 + 2.( - 6)} \over {98 + 2}} = 0,86(m/s)\)
b. Khi vật bay đến cùng chiều chuyển động của xe cát, thì v0 = 7 m/s, nên ta có :
\(V = \displaystyle{{98.1 + 2.6} \over {98 + 2}} = 1,1(m/s)\)
23.10.
Một quả lựu đạn, đang bay theo phương ngang với vận tốc 10 m/s, bị nổ , và tách thành hai mảnh có trọng lượng 10 N và 15 N. Sau khi nổ, mảnh to vẫn chuyển động theo phương ngang với vận tốc 25 m/s. Lấy g ~ 10 m/s2. Xác định vận tốc và phương chuyển động của mảnh nhỏ.
Phương pháp giải:
Áp dụng định luật bảo toàn động lượng \(\overrightarrow {{p_1}} + \overrightarrow {{p_2}} = \overrightarrow {p{'_1}} + \overrightarrow {p{'_2}} \)
Lời giải chi tiết:
Hệ vật gồm hai mảnh của quả lựu đạn là hệ cô lập, do không chịu tác dụng của ngoại lực, nên động lượng của hệ vật bảo toàn.
+ Trước khi nổ, hai mảnh của quả lựu đạn đều chuyển động với vận tốc v0, nên hệ vật có tổng động lượng :
p0 = (m1 + m2)v0.
+ Sau khi nổ, hệ vật có tổng động lượng :
p = m1v1 + m2v2
Áp dụng định luật bảo toàn động lượng cho hệ vật, ta có
p = p0 => m1v1 + m2v2 = (m1 + m2)v0
suy ra: \({v_1} = \displaystyle{{({m_1} + {m_2}){v_0} - {m_2}{v_2}} \over {{m_1}}}\)
Thay số, ta tìm được :
\({v_1} = \displaystyle{{({m_1} + {m_2}){v_0} - {m_2}{v_2}} \over {{m_1}}} \\= \displaystyle{{(1,0 + 1,5).10 - 1,5.25} \over {1,0}} \\= - 12,5(m/s)\)
Dấu (-) chứng tỏ sau khi nổ, vận tốc v1| của mảnh nhỏ ngược hướng với vận tốc ban đầu v0 của quả lựu đạn.
Loigiaihay.com













Danh sách bình luận