Đề thi học kì 1 Toán 11 - Đề số 10
Đề thi học kì 1 Toán 11 - Đề số 10
Đề bài
Phương trình \(\sin x = - \frac{1}{2}\) có tập nghiệm là
-
A.
\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
-
B.
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ;\frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)s
-
C.
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ;\frac{{7\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
-
D.
\(S = \left\{ {\frac{1}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
Đồ thị của hàm số y = cosx có tính chất nào dưới đây?
-
A.
Đối xứng qua gốc tọa độ
-
B.
Đối xứng qua trục hoành
-
C.
Đối xứng qua trục tung
-
D.
Đối xứng qua điểm I(0;1)
Cho cấp số cộng $(u_n)$ có $u_1 = 2$; công sai d = 5. Giá trị của $u_5$ là
-
A.
$u_5 = 22$.
-
B.
$u_5 = 12$.
-
C.
$u_5 = 27$.
-
D.
$u_5 = 32$.
Với giá trị x; y nào dưới đây thì các số hạng lần lượt là -2 ;x ; -18; y theo thứ tự đó lập thành một cấp số nhân?
-
A.
\(\left\{ \begin{array}{l}x = 6\\y = - 54\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x = - 10\\y = - 26\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = - 6\\y = - 54\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = - 6\\y = 54\end{array} \right.\)
Giới hạn \(\lim \frac{1}{{2n + 5}}\) bằng
-
A.
\(\frac{1}{2}\)
-
B.
0
-
C.
\( + \infty \)
-
D.
\(\frac{1}{5}\)
Cho hàm số $f(x)$ xác định trên ${\mathbb{R}},$ liên tục tại $x = 2$ và thỏa mãn $\lim\limits_{x\rightarrow 2}f(x) = 4.$ Khi đó ta phải gán $f(2)$ bằng bao nhiêu?
-
A.
$f(2) = - 1$.
-
B.
$f(2) = 1$.
-
C.
$f(2) = - 4$.
-
D.
$f(2) = 4$.
Cho mẫu số liệu ghép nhóm về thống kê nhiệt độ tại một địa điểm trong 40 ngày, ta có bảng số liệu sau:
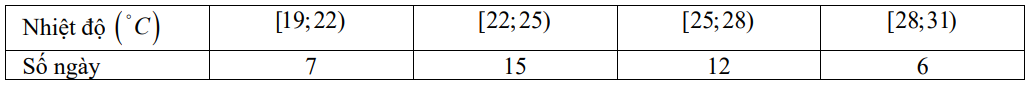
Có bao nhiêu ngày có nhiệt độ từ $28^{{^\circ}}C$ đến dưới $31^{{^\circ}}C$?
-
A.
7.
-
B.
4.
-
C.
5.
-
D.
6.
Điểm thi môn Toán trong Kỳ thi Tốt nghiệp trung học phổ thông của 690 học sinh trường THPT X được thống kê bởi bảng số liệu như sau:

Điểm trung bình môn Toán của mẫu số liệu trên xấp xỉ bằng
-
A.
5,4
-
B.
6,4
-
C.
7,4
-
D.
7,0
Cho $\lim\limits_{x\rightarrow 1}f(x) = - 3$ và $\lim\limits_{x\rightarrow 1}g(x) = 5.$ Giá trị của $\lim\limits_{x\rightarrow 1}\left\lbrack {f(x) + g(x)} \right\rbrack$ bằng
-
A.
$8$.
-
B.
$- 8$.
-
C.
$- 15$.
-
D.
$2$.
Cho bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại E.

Điểm E không thuộc mặt phẳng nào sao đây?
-
A.
(ACD).
-
B.
(BCD).
-
C.
(ABD).
-
D.
(CMN).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, AB.

Đường thẳng nào sau đây song song với đường thẳng CD?
-
A.
AN.
-
B.
MN.
-
C.
MP.
-
D.
NP.
Hai mặt phẳng (P) và (Q) được gọi là song song nếu
-
A.
Có một đường thẳng trong (P) song song với (Q).
-
B.
Có một đường thẳng trong (P) cắt (Q).
-
C.
Có hai đường thẳng trong (P) cùng song song với (Q).
-
D.
Chúng không có điểm chung.
Các mệnh đề sau đúng hay sai?
a) Hàm số $f(x) = \dfrac{3x - 1}{x + 2}$ liên tục trên các khoảng $( - \infty;2)$ và $(2; + \infty)$.
b) $\lim\limits_{x\rightarrow 2^{-}}\dfrac{4x + 1}{x - 2} = - \infty$.
c) $\lim\limits_{x\rightarrow - \infty}\dfrac{(2x + 1)(4 - 5x)}{- x^{2} + 7x + 8} = 10$.
d) Hàm số $f(x) = \tan 2x$ liên tục trên $\mathbb{R}$.
a) SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Giao điểm của đường thẳng AM và mặt phẳng (SBD) thuộc cạnh SO.
c) Đường thẳng MO cắt mặt phẳng (SAD).
d) Ba mặt phẳng (SAB), (SAC) và (MOB) đôi một cắt nhau theo ba giao tuyến phân biệt và ba giao tuyến này đồng quy.
Một vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút. Tại vị trí quan sát, bạn Linh thấy vòng quay chuyển động theo chiều kim đồng hồ. Khi vòng quay chuyển động được 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng bao nhiêu radian (làm tròn kết quả đến hàng phần mười)?
Một hội trường lớn có 35 ghế ở hàng đầu tiên, 37 ghế ở hàng thứ hai, 39 ghế ở hàng thứ ba và cứ tiếp tục theo quy luật như vậy. Có tất cả 27 hàng ghế. Hỏi hội trường đó có bao nhiêu ghế?
Trong hồ có chứa 12000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 40 gam / lít vào hồ với tốc độ 20 lít/phút. Nồng độ muối (gam/lít) trong hồ bằng bao nhiêu nếu bơm nước vào hồ một thời gian dài (xem như $t \to +\infty$).
Một công ty bất động sản Đất Vàng thực hiện cuộc khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào để tiến hành dự án xây nhà ở Thăng Long group sắp tới. Kết quả khảo sát 500 khách hàng được ghi lại ở bảng sau:

Công ty bất động sản Đất Vàng nên xây nhà ở mức giá nào để nhiều người có nhu cầu xây nhà?
Lời giải và đáp án
Phương trình \(\sin x = - \frac{1}{2}\) có tập nghiệm là
-
A.
\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
-
B.
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ;\frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)s
-
C.
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ;\frac{{7\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
-
D.
\(S = \left\{ {\frac{1}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
Đáp án : C
Áp dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\).
\(\sin x = - \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{6} + k2\pi \\x = \pi - \left( { - \frac{\pi }{6}} \right) + k2\pi = \frac{{7\pi }}{6} + k2\pi \end{array} \right.\) \(\left( {k \in \mathbb{Z}} \right)\).
Đồ thị của hàm số y = cosx có tính chất nào dưới đây?
-
A.
Đối xứng qua gốc tọa độ
-
B.
Đối xứng qua trục hoành
-
C.
Đối xứng qua trục tung
-
D.
Đối xứng qua điểm I(0;1)
Đáp án : C
Sử dụng tính chất của hàm số và đồ thị hàm số y = cosx.
Hàm số y = cosx là hàm số chẵn nên đồ thị đối xứng qua trục tung.
Cho cấp số cộng $(u_n)$ có $u_1 = 2$; công sai d = 5. Giá trị của $u_5$ là
-
A.
$u_5 = 22$.
-
B.
$u_5 = 12$.
-
C.
$u_5 = 27$.
-
D.
$u_5 = 32$.
Đáp án : A
Áp dụng công thức tính số hạng tổng quát của cấp số cộng \({u_n} = {u_{n-1}} + (n - 1)d\).
\({u_5} = 2 + (5 - 1).5 = 22\).
Với giá trị x; y nào dưới đây thì các số hạng lần lượt là -2 ;x ; -18; y theo thứ tự đó lập thành một cấp số nhân?
-
A.
\(\left\{ \begin{array}{l}x = 6\\y = - 54\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x = - 10\\y = - 26\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = - 6\\y = - 54\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = - 6\\y = 54\end{array} \right.\)
Đáp án : C
\({u_1};{u_2};{u_3}\) lập thành cấp số nhân có tính chất \(u_2^2 = {u_1}.{u_3}\).
Cấp số nhân -2; x; -18; y có
\(\left\{ {\begin{array}{*{20}{c}}{{x^2} = ( - 2).( - 18)}\\{{{( - 18)}^2} = xy}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x^2} = 36}\\{xy = 324}\end{array}} \right.\)
Với x = 6 thì y = 54.
Với x = -6 thì y = -54.
Vậy (x; y) = (6; 54) hoặc (x; y) = (-6; -54).
Giới hạn \(\lim \frac{1}{{2n + 5}}\) bằng
-
A.
\(\frac{1}{2}\)
-
B.
0
-
C.
\( + \infty \)
-
D.
\(\frac{1}{5}\)
Đáp án : B
Sử dụng quy tắc tính giới hạn của dãy số.
Ta có \(\lim (2n + 5) = + \infty \) suy ra \(\lim \frac{1}{{2n + 5}} = 0\).
Cho hàm số $f(x)$ xác định trên ${\mathbb{R}},$ liên tục tại $x = 2$ và thỏa mãn $\lim\limits_{x\rightarrow 2}f(x) = 4.$ Khi đó ta phải gán $f(2)$ bằng bao nhiêu?
-
A.
$f(2) = - 1$.
-
B.
$f(2) = 1$.
-
C.
$f(2) = - 4$.
-
D.
$f(2) = 4$.
Đáp án : D
Hàm số liên tục tại \(x_0\) khi \(\mathop {\lim }\limits_{x \to x_0} f\left( x \right) = f(x_0) \).
Hàm số liên tục tại x = 2 nên \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f(2) = 4\).
Cho mẫu số liệu ghép nhóm về thống kê nhiệt độ tại một địa điểm trong 40 ngày, ta có bảng số liệu sau:
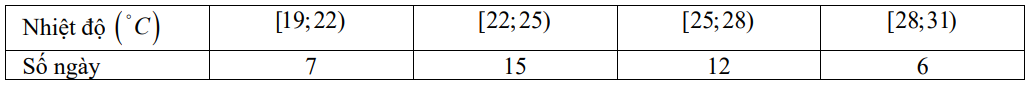
Có bao nhiêu ngày có nhiệt độ từ $28^{{^\circ}}C$ đến dưới $31^{{^\circ}}C$?
-
A.
7.
-
B.
4.
-
C.
5.
-
D.
6.
Đáp án : D
Đọc bảng số liệu.
Có 6 ngày có nhiệt độ từ $28^{{^\circ}}C$ đến dưới $31^{{^\circ}}C$.
Điểm thi môn Toán trong Kỳ thi Tốt nghiệp trung học phổ thông của 690 học sinh trường THPT X được thống kê bởi bảng số liệu như sau:

Điểm trung bình môn Toán của mẫu số liệu trên xấp xỉ bằng
-
A.
5,4
-
B.
6,4
-
C.
7,4
-
D.
7,0
Đáp án : B
Công thức tìm giá trị trung bình.
Ta có \(\bar x = \frac{{15.1 + 55.3 + 190.5 + 290.7 + 140.9}}{{15 + 55 + 190 + 290 + 140}} = 6,4\).
Cho $\lim\limits_{x\rightarrow 1}f(x) = - 3$ và $\lim\limits_{x\rightarrow 1}g(x) = 5.$ Giá trị của $\lim\limits_{x\rightarrow 1}\left\lbrack {f(x) + g(x)} \right\rbrack$ bằng
-
A.
$8$.
-
B.
$- 8$.
-
C.
$- 15$.
-
D.
$2$.
Đáp án : D
Áp dụng tính chất giới hạn của hàm số.
\(\mathop {\lim }\limits_{x \to 1} \left[ {f(x) + f(x)} \right] = \mathop {\lim }\limits_{x \to 1} f(x) + \mathop {\lim }\limits_{x \to 1} g(x) = - 3 + 5 = 2\).
Cho bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại E.

Điểm E không thuộc mặt phẳng nào sao đây?
-
A.
(ACD).
-
B.
(BCD).
-
C.
(ABD).
-
D.
(CMN).
Đáp án : A
Nếu \(E \in d\) và \(d \subset (P)\) thì \(E \in (P)\).
\(E \in BD \subset (BCD)\), \(E \in BD \subset (ABD)\), \(E \in MN \subset (CMN)\), \(E \notin (ACD)\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, AB.

Đường thẳng nào sau đây song song với đường thẳng CD?
-
A.
AN.
-
B.
MN.
-
C.
MP.
-
D.
NP.
Đáp án : B
Áp dụng tính chất đường trung bình.
MN là đường trung bình của tam giác SAB nên MN // AB. Mà ABCD là hình bình hành nên AB // CD. Do đó MN // CD.
Hai mặt phẳng (P) và (Q) được gọi là song song nếu
-
A.
Có một đường thẳng trong (P) song song với (Q).
-
B.
Có một đường thẳng trong (P) cắt (Q).
-
C.
Có hai đường thẳng trong (P) cùng song song với (Q).
-
D.
Chúng không có điểm chung.
Đáp án : D
Dựa vào định nghĩa hai mặt phẳng song song.
Hai mặt phẳng (P) và (Q) được gọi là song song nếu chúng không có điểm chung.
Các mệnh đề sau đúng hay sai?
a) Hàm số $f(x) = \dfrac{3x - 1}{x + 2}$ liên tục trên các khoảng $( - \infty;2)$ và $(2; + \infty)$.
b) $\lim\limits_{x\rightarrow 2^{-}}\dfrac{4x + 1}{x - 2} = - \infty$.
c) $\lim\limits_{x\rightarrow - \infty}\dfrac{(2x + 1)(4 - 5x)}{- x^{2} + 7x + 8} = 10$.
d) Hàm số $f(x) = \tan 2x$ liên tục trên $\mathbb{R}$.
a) Hàm số $f(x) = \dfrac{3x - 1}{x + 2}$ liên tục trên các khoảng $( - \infty;2)$ và $(2; + \infty)$.
b) $\lim\limits_{x\rightarrow 2^{-}}\dfrac{4x + 1}{x - 2} = - \infty$.
c) $\lim\limits_{x\rightarrow - \infty}\dfrac{(2x + 1)(4 - 5x)}{- x^{2} + 7x + 8} = 10$.
d) Hàm số $f(x) = \tan 2x$ liên tục trên $\mathbb{R}$.
Hàm số y = f(x) được gọi là liên tục trên khoảng (a;b) nếu mà hàm số liên tục tại mọi điểm thuộc khoảng đó.
Áp dụng các quy tắc tính giới hạn của hàm số.
a) Đúng. Hàm số có TXĐ là \(D = \mathbb{R}\backslash \{ - 2\} \) nên liên tục trên các khoảng $(-\infty ;2)$ và $(2;+\infty )$.
b) Đúng. \(\mathop {\lim }\limits_{x \to {2^ - }} (4x + 1) = \mathop {\lim }\limits_{x \to {2^ - }} (4.2 + 1) = 9 > 0\);
\(\mathop {\lim }\limits_{x \to {2^ - }} (x - 2) = \mathop {\lim }\limits_{x \to {2^ - }} (x - 2) = 2 - 2 = 0\) và \(x - 2 < 0\).
Do đó \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{4x + 1}}{{x - 2}} = - \infty \).
c) Đúng. \(\mathop {\lim }\limits_{x \to - \infty } \frac{{(2x + 1)(4 - 5x)}}{{ - {x^2} + 7x + 8}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 10{x^2} + 3x + 4}}{{ - {x^2} + 7x + 8}}\)
\( = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2}\left( { - 10 + \frac{3}{x} + \frac{4}{{{x^2}}}} \right)}}{{{x^2}\left( { - 1 + \frac{7}{x} + \frac{8}{{{x^2}}}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 10 + \frac{3}{x} + \frac{4}{{{x^2}}}}}{{ - 1 + \frac{7}{x} + \frac{8}{{{x^2}}}}} = \frac{{ - 10}}{{ - 1}} = 10\).
d) Sai. Hàm số tan không liên tục trên \(\mathbb{R}\).
a) SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Giao điểm của đường thẳng AM và mặt phẳng (SBD) thuộc cạnh SO.
c) Đường thẳng MO cắt mặt phẳng (SAD).
d) Ba mặt phẳng (SAB), (SAC) và (MOB) đôi một cắt nhau theo ba giao tuyến phân biệt và ba giao tuyến này đồng quy.
a) SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Giao điểm của đường thẳng AM và mặt phẳng (SBD) thuộc cạnh SO.
c) Đường thẳng MO cắt mặt phẳng (SAD).
d) Ba mặt phẳng (SAB), (SAC) và (MOB) đôi một cắt nhau theo ba giao tuyến phân biệt và ba giao tuyến này đồng quy.
Áp dụng điều kiện và tính chất của hai đường thẳng song song.

a) Đúng. Ta có \(\left\{ \begin{array}{l}S \in (SAC) \cap (SBD)\\O \in AC \subset (SAC)\\O \in BD \subset (SBD)\end{array} \right. \Rightarrow (SAC) \cap (SBD) = SO\).
b) Đúng. Xét mặt phẳng (SAC), giả sử AM cắt SO tại G. Khi đó \(\left\{ \begin{array}{l}G \in AM\\G \in SO \subset (SBD)\end{array} \right.\) nên G là giao điểm của AM và (SBD).
c) Sai. Xét tam giác SAC có MO là đường trung bình, khi đó MO // SA, suy ra MO // (SAC).
d) Sai. \(\left\{ \begin{array}{l}(SAB) \cap (SAC) = SA\\(SAC) \cap (MOB) = MO\\SA//MO\end{array} \right. \Rightarrow \) (SAB), (SAC) và (MOB) đôi một cắt nhau theo ba giao tuyến phân biệt và ba giao tuyến này song song.
Một vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút. Tại vị trí quan sát, bạn Linh thấy vòng quay chuyển động theo chiều kim đồng hồ. Khi vòng quay chuyển động được 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng bao nhiêu radian (làm tròn kết quả đến hàng phần mười)?
Tìm số đo góc lượng giác vòng quay quay được trong 1 phút, từ đó tính số đo góc lượng giác vòng quay quay được trong 15 phút.
Do vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút và chuyển động theo chiều kim đồng hồ nên sau 15 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng \( - 2\pi \) (rad) .
Do đó, sau 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng:
\(\frac{{ - 2\pi }}{{15}} \cdot 10 = \frac{{ - 4\pi }}{3} \approx - 4,2\) (rad).
Một hội trường lớn có 35 ghế ở hàng đầu tiên, 37 ghế ở hàng thứ hai, 39 ghế ở hàng thứ ba và cứ tiếp tục theo quy luật như vậy. Có tất cả 27 hàng ghế. Hỏi hội trường đó có bao nhiêu ghế?
Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng: \({S_n} = \frac{{\left[ {2{u_1} + (n - 1)d} \right]n}}{2}\).
Gọi \(u_n\) là số ghế ở hàng thứ n. Vì hội trường lớn có 35 ghế ở hàng đầu tiên, 37 ghế ở hàng thứ hai, 39 ghế ở hàng thứ ba, nên dãy số $(u_n)$ lập thành cấp số cộng có $u_1 = 35$ và công sai d = 2. Suy ra tổng số ghế của hội trường với 27 hàng ghế là:
$S_{27} = \frac{(2u_1 + 26d) . 27}{2} = 1647$ (ghế).
Trong hồ có chứa 12000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 40 gam / lít vào hồ với tốc độ 20 lít/phút. Nồng độ muối (gam/lít) trong hồ bằng bao nhiêu nếu bơm nước vào hồ một thời gian dài (xem như $t \to +\infty$).
Lập hàm số nồng độ muối C(t) rồi tính $\lim_{t \to +\infty} C(t)$.
Thể tích nước biển bơm vào sau t phút là: 20t (lít).
Khối lượng muối là: 40.20t = 800t (gam).
Thể tích hồ sau khi bơm nước biển vào là: 12000 + 20t (lít).
Nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là: $C(t) = \frac{800t}{12000 + 20t} = \frac{40t}{600 + t}$ (gam/lít).
Ta có: $\lim_{t \to +\infty} C(t) = \lim_{t \to +\infty} \frac{40t}{600 + t} = 40$ (gam/lít).
Vậy khi bơm nước vào hồ một thời gian dài thì nồng độ muối trong hồ bằng 40 (gam/lít), tương đương với nồng độ muối trong nước biển.
Một công ty bất động sản Đất Vàng thực hiện cuộc khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào để tiến hành dự án xây nhà ở Thăng Long group sắp tới. Kết quả khảo sát 500 khách hàng được ghi lại ở bảng sau:

Công ty bất động sản Đất Vàng nên xây nhà ở mức giá nào để nhiều người có nhu cầu xây nhà?
Áp dụng công thức tính mốt của mẫu số liệu ghép nhóm:
\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g\).
Nhóm chứa mốt của mẫu số liệu trên là [18; 22).
Do đó:
$u_m = 18; n_{m-1} = 105; n_{m+1} = 96; u_{m+1} - u_m = 22 - 18 = 4$.
Mốt của mẫu số liệu ghép nhóm là:
$M_o = 18 + \frac{179 - 105}{(179 - 105) + (179 - 96)} \cdot 4 \approx 19,9$.
Dựa vào kết quả trên ta có thể dự đoán rằng nếu công ty bất động sản Đất Vàng xây nhà ở mức giá 19,9 triệu đồng/ mét vuông thì sẽ có nhiều người mua nhất.
Xác định số hạng đầu và công bội của cấp số nhân, áp dụng công thức ${{u}_{n}}={{u}_{1}}{{q}^{n-1}}$.
Áp dụng quy tắc tính giới hạn của hàm số.
a) Vì cứ sau 1 chu kì bán rã thì khối lượng mẫu chất phóng xạ giảm một nửa nên $(u_n)$ là cấp số nhân với $u_1 = 21$ và công bội $q = \frac{1}{2}$.
Khi đó, số hạng tổng quát của dãy số $(u_n)$ là: $u_n = \frac{42}{2^n}$.
b) Ta có: $\lim_{n \to \infty} u_n = \lim_{n \to \infty} \frac{42}{2^n} = \lim_{n \to \infty} 42 . \lim_{n \to \infty} \left( \frac{1}{2} \right)^n = 42 . 0 = 0$.
Từ giới hạn đó, ta rút ra được ý nghĩa: Khi $n$ càng dần tới vô cực thì khối lượng còn lại của mẫu chất phóng xạ càng dần về 0, nghĩa là sau một khoảng thời gian đủ dài thì khối lượng còn lại của mẫu chất phóng xạ là rất nhỏ (đến mức không đáng kể).
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
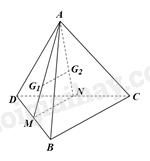
Gọi M, N lần lượt là trung điểm của DB, DC. Do đó, MN là đường trung bình của tam giác DBC. Suy ra MN//BC (1)
Vì \({G_1}\) là trọng tâm của tam giác ADB nên \(\frac{{A{G_1}}}{{AM}} = \frac{2}{3}\).
Vì \({G_2}\) là trọng tâm của tam giác ADC nên \(\frac{{A{G_2}}}{{AN}} = \frac{2}{3}\).
Tam giác AMN có: \(\frac{{A{G_1}}}{{AM}} = \frac{{A{G_2}}}{{AN}}\left( { = \frac{2}{3}} \right)\) nên \({G_1}{G_2}//MN\) (2) (định lí Thalès đảo)
Từ (1) và (2) ta có: \({G_1}{G_2}//MN//BC\).
Vì \({G_1}{G_2}//BC\), \({G_1}{G_2}\) không nằm trong mặt phẳng (ABC), \(BC \subset \left( {ABC} \right)\) nên \({G_1}{G_2}\)//(ABC)
Vì \({G_1}{G_2}//BC\), \({G_1}{G_2}\) không nằm trong mặt phẳng (DBC), \(BC \subset \left( {DBC} \right)\) nên \({G_1}{G_2}\)//(DBC).
Ta có bảng số liệu ghép nhóm:

Để tính tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm trước hết ta xác định nhóm chứa \({Q_3}.\) Giả sử đó là nhóm thứ p: \(\left[ {{a_p};{a_{p + 1}}} \right)\).
Khi đó, \({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + ... + {m_{p - 1}}} \right)}}{{{m_p}}}\left( {{a_{p + 1}} - {a_p}} \right)\), trong đó n là cỡ mẫu, với \(p = 1\) thì ta quy ước \({m_1} + ... + {m_{p - 1}} = 0\)
Số a chính là tứ phân vị thứ ba.
Tứ phân vị thứ ba a là \(\frac{{{x_{18}} + {x_{19}}}}{2}\). Do \({x_{18}},{x_{19}}\) đều thuộc nhóm \(\left[ {8;10} \right)\) nên nhóm này chứa a. Do đó, \(p = 4,{a_4} = 8,{m_4} = 9,{m_1} + {m_2} + {m_3} = 2 + 5 + 6 = 13,{a_5} - {a_4} = 2\)
Suy ra: \(a = 8 + \frac{{\frac{{3.25}}{4} - 13}}{9}.2 = \frac{{167}}{{18}}\).
Đề thi học kì 1 Toán 11 - Đề số 9
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng (với giả thiết các biểu thức đều có nghĩa).
Phần trắc nghiệm (7 điểm) Câu 1: Nghiệm của phương trình
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (7 điểm) Câu 1: Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là
A. Nội dung ôn tập Hàm số lượng giác và phương trình lượng giác 1. Giá trị lượng giác của góc lượng giác 2. Công thức lượng giác 3. Hàm số lượng giác 4. Phương trình lượng giác cơ bản
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |












Danh sách bình luận