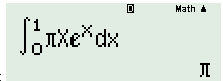50 bài tập trắc nghiệm tích phân mức độ nhận biết
Làm đề thiCâu hỏi 1 :
Cho \(\int\limits_0^1 {f\left( x \right)dx} = - 2\) và \(\int\limits_0^1 {g\left( x \right)dx} = - 5\), khi đó \(\int\limits_0^1 {\left[ {f\left( x \right) + 3g\left( x \right)} \right]dx} \) bằng:
- A \( - 10\)
- B \(12\)
- C \( - 17\)
- D \(1\)
Đáp án: C
Phương pháp giải:
Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {mf\left( x \right) + ng\left( x \right)} \right]dx} = m\int\limits_a^b {f\left( x \right)dx} + n\int\limits_a^b {g\left( x \right)dx} \).
Lời giải chi tiết:
\(\int\limits_0^1 {\left[ {f\left( x \right) + 3g\left( x \right)} \right]dx} = \int\limits_0^1 {f\left( x \right)dx} + 3\int\limits_0^1 {g\left( x \right)dx} \)\( = - 2 + 3.\left( { - 5} \right) = - 17\).
Chọn C.
Câu hỏi 2 :
Giá trị của \(\int\limits_0^\pi {\left( {2\cos x - \sin 2x} \right)dx} \) là:
- A \(1\).
- B \(0\).
- C \( - 1\).
- D \( - 2\).
Đáp án: B
Phương pháp giải:
Sử dụng các công thức nguyên hàm hàm số lượng giác: \(\int {\sin kxdx} = - \dfrac{1}{k}\cos kx + C\), \(\int {\cos kxdx} = \dfrac{1}{k}\sin kx + C\).
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,\,\,\int\limits_0^\pi {\left( {2\cos x - \sin 2x} \right)dx} \\ = \left. {\left( {2\sin x + \dfrac{1}{2}\cos 2x} \right)} \right|_0^\pi \\ = 2\sin \pi + \dfrac{1}{2}\cos 2\pi - 2\sin 0 - \dfrac{1}{2}\cos 0\\ = \dfrac{1}{2} - \dfrac{1}{2} = 0\end{array}\)
Chọn B.
Câu hỏi 3 :
Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\left[ { - 1;4} \right],\,\,f\left( 4 \right) = 2019,\,\,\int\limits_{ - 1}^4 {f'\left( x \right){\rm{d}}x} = 2020.\) Tính \(f\left( { - 1} \right)\)?
- A \(f\left( { - 1} \right) = - 1\)
- B \(f\left( { - 1} \right) = 1\)
- C \(f\left( { - 1} \right) = 3\)
- D \(f\left( { - 1} \right) = 2\)
Đáp án: A
Phương pháp giải:
Sử dụng tính chất của tích phân để làm bài toán: \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right).\)
Lời giải chi tiết:
Theo đề bài ta có: \(\int\limits_{ - 1}^4 {f'\left( x \right)dx} = 2020\)
\(\begin{array}{l} \Leftrightarrow f\left( 4 \right) - f\left( { - 1} \right) = 2020\\ \Leftrightarrow f\left( { - 1} \right) = f\left( 4 \right) - 2020\\ \Leftrightarrow f\left( { - 1} \right) = 2019 - 2020 = - 1.\end{array}\)
Chọn A.
Câu hỏi 4 :
Tính tích phân \(I = \int\limits_0^2 {\left| {1 - x} \right|dx} \) ta được kết quả:
- A \(\dfrac{1}{2}\)
- B \(1\)
- C \(\dfrac{3}{2}\)
- D \(2\)
Đáp án: B
Phương pháp giải:
- Xét dấu của biểu thức \(1 - x\) trên \(\left[ {0;2} \right]\) và phá trị tuyệt đối.
- Sử dụng các nguyên hàm cơ bản để tính tích phân.
Lời giải chi tiết:
\(\begin{array}{l}I = \int\limits_0^2 {\left| {1 - x} \right|dx} = \int\limits_0^1 {\left| {1 - x} \right|dx} + \int\limits_1^2 {\left| {1 - x} \right|dx} \\\,\,\,\, = \int\limits_0^1 {\left( {1 - x} \right)dx} - \int\limits_1^2 {\left( {1 - x} \right)dx} \\\,\,\,\, = \left. {\left( {x - \dfrac{{{x^2}}}{2}} \right)} \right|_0^1 - \left. {\left( {x - \dfrac{{{x^2}}}{2}} \right)} \right|_1^2\\\,\,\,\, = \dfrac{1}{2} - \left( {0 - \dfrac{1}{2}} \right) = 1\end{array}\).
Chọn B.
Câu hỏi 5 :
Tính tích phân \(I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{\sin 2x}{1+{{\sin }^{2}}x}dx}\) ta được:
- A ln2
- B 0
- C ln3
- D \(\frac{\pi }{2}\)
Đáp án: A
Phương pháp giải:
Sử dụng phương pháp đặt ẩn phụ, đặt \(t={{\sin }^{2}}x\)
Lời giải chi tiết:
\(I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{\sin 2x}{1+{{\sin }^{2}}x}dx}=I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{2\sin x\cos x}{1+{{\sin }^{2}}x}dx}\)
Đặt \(t={{\sin }^{2}}x\Leftrightarrow dt=2\sin x\cos xdx\).
Đổi cận \(\left\{ \begin{array}{l}x = 0 \Leftrightarrow t = 0\\x = \frac{\pi }{2} \Leftrightarrow t = 1\end{array} \right.,\) khi đó ta có: \(I = \int\limits_0^1 {\frac{{dt}}{{1 + t}}} = \left. {\ln \left| {1 + t} \right|} \right|_0^1 = \ln 2 - \ln 1 = \ln 2\)
Chọn A.
Câu hỏi 6 :
Tính tích phân \(I=\int\limits_{1}^{2}{\frac{{{x}^{2}}+2\ln x}{x}dx}\) ta được:
- A \(\frac{3}{2}+2\ln 2\)
- B \(\frac{3}{2}+{{\ln }^{2}}2\)
- C \(\frac{2}{3}+2\ln 2\)
- D \(\frac{3}{2}+\ln 2\)
Đáp án: B
Phương pháp giải:
Sử dụng phương pháp đăt ẩn phụ, đặt \(t=\ln x\)
Lời giải chi tiết:
Đặt \(t=\ln x\Leftrightarrow dt=\frac{dx}{x}\) và \(x={{e}^{t}}\)
Đổi cận \(\left\{ \begin{array}{l}x = 1 \Leftrightarrow t = 0\\x = 2 \Leftrightarrow t = \ln 2\end{array} \right.\), khi đó
\(I=\int\limits_{1}^{2}{\frac{{{x}^{2}}+2\ln x}{x}dx}=\int\limits_{0}^{\ln 2}{\left( {{e}^{2t}}+2t \right)dt}=\left. \left( \frac{1}{2}{{e}^{2t}}+{{t}^{2}} \right) \right|_{0}^{\ln 2}=2+{{\ln }^{2}}2-\frac{1}{2}=\frac{3}{2}+{{\ln }^{2}}2\)
Chọn B.
Câu hỏi 7 :
Biết \(f(x)\) là hàm liên tục trên \(\mathbb{R}\) và \(\int\limits_{0}^{9}{f(x)dx=9}\). Khi đó giá trị của \(\int\limits_{1}^{4}{f(3x-3)dx}\) là
- A 27
- B 3
- C 24
- D 0
Đáp án: B
Phương pháp giải:
Tính tích phân bằng phương pháp đổi biến.
Lời giải chi tiết:
Đặt \(3x-3=y\Rightarrow 3dx=dy\Leftrightarrow dx=\frac{dy}{3}\)
Đổi cận:
![]()
\(I=\int\limits_{1}^{4}{f(3x-3)dx}=\frac{1}{3}\int\limits_{0}^{9}{f(y)dy}=\frac{1}{3}\int\limits_{0}^{9}{f(x)dx=\frac{1}{3}.9=3}\)
Chọn: B.
Câu hỏi 8 :
Tích phân \(I=\int\limits_{1}^{e}{\frac{dx}{x-3}}\) bằng:
- A \(\ln \frac{3-e}{2}\)
- B \(\ln \frac{3-e}{4}\)
- C \(\ln \frac{3+e}{4}\)
- D \(\ln \frac{e-3}{2}\)
Đáp án: A
Phương pháp giải:
\(\int{\frac{1}{ax+b}dx}=\frac{1}{a}\ln \left| ax+b \right|+C\)
Lời giải chi tiết:
\(I=\int\limits_{1}^{e}{\frac{dx}{x-3}}=\left. \ln \left| x-3 \right| \right|_{1}^{e}=\ln \left| e-3 \right|-\ln 2=\ln \frac{3-e}{2}\)
Chọn A.
Câu hỏi 9 :
Biết \(\int\limits_{1}^{3}{\frac{1}{2x+3}dx}=m\ln 5+n\ln 3\,\,\left( m,n\in R \right)\). Tính \(P=m-n\)
- A P = 0
- B P = -1
- C \(P=\frac{3}{2}\)
- D \(P=-\frac{3}{2}\)
Đáp án: D
Phương pháp giải:
\(\int{\frac{1}{ax+b}dx}=\frac{1}{a}\ln \left| ax+b \right|+C\)
Lời giải chi tiết:
\(\begin{array}{l}
\int\limits_1^3 {\frac{1}{{2x + 3}}dx} = \left. {\frac{1}{2}\ln \left| {2x + 3} \right|} \right|_1^3\\
= \frac{1}{2}\left( {\ln 9 - \ln 5} \right) = \ln 3 - \frac{1}{2}\ln 5\\
\Rightarrow n = 1;\,\,\,m = - \frac{1}{2}\\
\Rightarrow P = m - n = - \frac{1}{2} - 1 = - \frac{3}{2}
\end{array}\)
Chọn D.
Câu hỏi 10 :
Tính tích phân \(\int\limits_{0}^{1}{\frac{dx}{{{x}^{2}}-x-12}}\)
- A \(\ln \frac{9}{16}\)
- B \(\frac{1}{4}\ln \frac{9}{16}\)
- C \(-\frac{1}{7}\ln \frac{9}{16}\)
- D \(\frac{1}{7}\ln \frac{9}{16}\)
Đáp án: D
Phương pháp giải:
\(\frac{1}{{{x}^{2}}-x-12}=\frac{1}{\left( x-4 \right)\left( x+3 \right)}=\frac{A}{x-4}+\frac{B}{x+3}\)
Lời giải chi tiết:
Ta có : \(\frac{1}{{{x}^{2}}-x-12}=\frac{1}{\left( x-4 \right)\left( x+3 \right)}=\frac{1}{7}\left( \frac{1}{x-4}-\frac{1}{x+3} \right)\)
\(\Rightarrow I=\frac{1}{7}\int\limits_{0}^{1}{\left( \frac{1}{x-4}-\frac{1}{x+3} \right)dx}=\left. \frac{1}{7}\ln \left| \frac{x-4}{x+3} \right| \right|_{0}^{1}=\frac{1}{7}\left( \ln \frac{3}{4}-\ln \frac{4}{3} \right)=\frac{1}{7}\ln \frac{9}{16}\)
Chọn D.
Câu hỏi 11 :
Cho \(\int\limits_{0}^{1}{\left( \frac{1}{x+1}-\frac{1}{x+2} \right)dx}=a\ln 2+b\ln 3\) với a, b là các số nguyên. Mệnh đề nào dưới đây đúng ?
- A \(a+b=2\)
- B \(a-2b=0\)
- C \(a+b=-2\)
- D \(a+2b=0\)
Đáp án: D
Phương pháp giải:
\(\int{\frac{1}{ax+b}dx}=\frac{1}{a}\ln \left| ax+b \right|+C\)
Lời giải chi tiết:
\(\begin{array}{l}\int\limits_0^1 {\left( {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}} \right)dx} = \left. {\left( {\ln \left| {x + 1} \right| - \ln \left| {x + 2} \right|} \right)} \right|_0^1 = \left. {\ln \left| {\frac{{x + 1}}{{x + 2}}} \right|} \right|_0^1 = \ln \frac{2}{3} - \ln \frac{1}{2} = \ln 2 - \ln 3 + \ln 2 = 2\ln 2 - \ln 3\\ \Rightarrow \left\{ \begin{array}{l}a = 2\\b = - 1\end{array} \right. \Rightarrow a + 2b = 2 - 2 = 0\end{array}\)
Chọn D.
Câu hỏi 12 :
Tính tích phân \(I = \int\limits_0^2 {{x^2}\sqrt {{x^3} + 1} dx} \)
- A \({{16} \over 9}\)
- B \( - {{16} \over 9}\)
- C \({{52} \over 9}\)
- D \( - {{52} \over 9}\)
Đáp án: C
Phương pháp giải:
Đặt ẩn phụ \(t = \sqrt {{x^3} + 1} \)
Lời giải chi tiết:
Đặt \(t = \sqrt {{x^3} + 1} \Leftrightarrow {t^2} = {x^3} + 1 \Leftrightarrow 2tdt = 3{x^2}dx \Leftrightarrow {x^2}dx = {2 \over 3}tdt\)
Đổi cận \(\left\{ \matrix{ x = 0 \Rightarrow t = 1 \hfill \cr x = 2 \Rightarrow t = 3 \hfill \cr} \right.\), khi đó ta có: \(I = \int\limits_1^3 {{{2{t^2}} \over 3}dt} = \left. {{2 \over 3}.{{{t^3}} \over 3}} \right|_1^3 = 6 - {2 \over 9} = {{52} \over 9}\)
Chọn C.
Câu hỏi 13 :
Biến đổi \(\int\limits_0^3 {{x \over {1 + \sqrt {1 + x} }}dx} \) thành \(\int\limits_1^2 {f\left( t \right)dt} \) , với \(t = \sqrt {1 + x} \). Khi đó \(f\left( t \right)\) là hàm số nào trong các hàm số sau đây?
- A \(f\left( t \right) = 2{t^2} - 2t\)
- B \(f\left( t \right) = {t^2} + t\)
- C \(f\left( t \right) = {t^2} - t\)
- D \(f\left( t \right) = 2{t^2} + 2t\)
Đáp án: A
Phương pháp giải:
Đặt \(t = \sqrt {1 + x} \)
Lời giải chi tiết:
Đặt \(t = \sqrt {1 + x} \Leftrightarrow {t^2} = 1 + x \Leftrightarrow 2tdt = dx\) và \(x = {t^2} - 1\), đổi cận \(\left\{ \matrix{ x = 0 \Rightarrow t = 1 \hfill \cr x = 3 \Rightarrow t = 2 \hfill \cr} \right.\), khi đó ta có: \(I = \int\limits_1^2 {{{{t^2} - 1} \over {1 + t}}2tdt} = \int\limits_1^2 {2t\left( {t - 1} \right)dt} = \int\limits_1^2 {\left( {2{t^2} - 2t} \right)dt} \Rightarrow f\left( t \right) = 2{t^2} - 2t\).
Chọn A.
Câu hỏi 14 :
Nếu \(\int\limits_{0}^{1}{f\left( x \right)\,\text{d}x}=5\) và \(\int\limits_{1}^{2}{f\left( x \right)\,\text{d}x}=2\) thì \(\int\limits_{0}^{2}{f\left( x \right)\,\text{d}x}\) bằng
- A
\(3.\)
- B
\(10.\)
- C
\(7.\)
- D \(\frac{5}{2}.\)
Đáp án: C
Phương pháp giải:
Sử dụng lý thuyết tích phân \(\int\limits_{a}^{c}{f\left( x \right)\,\text{d}x}+\int\limits_{c}^{b}{f\left( x \right)\,\text{d}x}=\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}.\)
Lời giải chi tiết:
Ta có \(\int\limits_{0}^{2}{f\left( x \right)\,\text{d}x}=\int\limits_{0}^{1}{f\left( x \right)\,\text{d}x}+\int\limits_{1}^{2}{f\left( x \right)\,\text{d}x}=5+2=7.\)
Chọn C
Câu hỏi 15 :
Cho \(I = \int\limits_{{\pi \over 6}}^{{\pi \over 4}} {{{dx} \over {{{\cos }^2}x{{\sin }^2}x}}} = a + b\sqrt 3 \) với a, b là số hữu tỉ. Tính giá trị a – b.
- A \( - {1 \over 3}\)
- B \( - {2 \over 3}\)
- C \({1 \over 3}\)
- D \({2 \over 3}\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức nhân đôi \(\sin 2x = 2\sin x\cos x\)
Lời giải chi tiết:
\(I = \int\limits_{{\pi \over 6}}^{{\pi \over 4}} {{{dx} \over {{{\cos }^2}x{{\sin }^2}x}}} = \int\limits_{{\pi \over 6}}^{{\pi \over 4}} {{{4dx} \over {{{\sin }^2}2x}}} = \left. { - 2\cot 2x} \right|_{{\pi \over 6}}^{{\pi \over 4}} = - 2\left( {0 - {1 \over {\sqrt 3 }}} \right) = {2 \over {\sqrt 3 }} = {{2\sqrt 3 } \over 3} \Rightarrow \left\{ \matrix{ a = 0 \hfill \cr b = {2 \over 3} \hfill \cr} \right. \Rightarrow a - b = - {2 \over 3}\)
Chọn B.
Câu hỏi 16 :
Tính tích phân \(I = \int\limits_{ - {\pi \over 2}}^{{\pi \over 6}} {\left( {\sin 2x - \cos 3x} \right)dx} \)
- A \(I = {2 \over 3}\)
- B \(I = {3 \over 4}\)
- C \(I = - {3 \over 4}\)
- D \(I = {9 \over {16}}\)
Đáp án: C
Phương pháp giải:
Sử dụng bảng nguyên hàm cơ bản.
Lời giải chi tiết:
\(I = \int\limits_{ - {\pi \over 2}}^{{\pi \over 6}} {\left( {\sin 2x - \cos 3x} \right)dx} = \left. {\left( { - {{\cos 2x} \over 2} - {{\sin 3x} \over 3}} \right)} \right|_{ - {\pi \over 2}}^{{\pi \over 6}} = {{ - 7} \over {12}} - {1 \over 6} = - {3 \over 4}\)
Chọn C.
Câu hỏi 17 :
Tính \(I=\int\limits_{0}^{1}{{{e}^{3x}}dx}\).
- A \(I=e-1\).
- B \(I={{e}^{3}}-1\).
- C \(\frac{{{e}^{3}}-1}{3}\).
- D \({{e}^{3}}+\frac{1}{2}\).
Đáp án: C
Phương pháp giải:
\(\int\limits_{{}}^{{}}{{{e}^{kx}}dx}=\frac{1}{k}{{e}^{kx}}+C\)
Lời giải chi tiết:
\(I=\int\limits_{0}^{1}{{{e}^{3x}}dx}=\frac{1}{3}\left. {{e}^{3x}} \right|_{0}^{1}=\frac{{{e}^{3}}-1}{3}\)
Chọn: C
Câu hỏi 18 :
Cho hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( a;c \right),\) \(a<b<c\) và \(\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}=5,\,\,\int\limits_{c}^{b}{f\left( x \right)\,\text{d}x}=1.\) Tính tích phân \(I=\int\limits_{a}^{c}{f\left( x \right)\,\text{d}x}.\)
- A \(I=4.\)
- B \(I=5.\)
- C \(I=6.\)
- D \(I=-\,5.\)
Đáp án: A
Phương pháp giải:
Sử dụng tích chất của tích phân : Với \(a<b<c\) ta có : \(\int\limits_{a}^{c}{f\left( x \right)dx=}\int\limits_{a}^{b}{f\left( x \right)dx}+\int\limits_{b}^{c}{f\left( x \right)dx.}\)
Lời giải chi tiết:
Ta có \(I=\int\limits_{a}^{c}{f\left( x \right)\,\text{d}x}=\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}+\int\limits_{b}^{c}{f\left( x \right)\,\text{d}x}=\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}-\int\limits_{c}^{b}{f\left( x \right)\,\text{d}x}=5-1=4.\)
Chọn A
Câu hỏi 19 :
Tích phân \(I=\int\limits_{0}^{1}{{{e}^{x\,+\,1}}\,\text{d}x}\) bằng
- A \({{e}^{2}}-1.\)
- B \({{e}^{2}}-e.\)
- C \({{e}^{2}}+e.\)
- D \(e-{{e}^{2}}.\)
Đáp án: B
Phương pháp giải:
Đổi biến số hoặc bấm máy tính
Lời giải chi tiết:
Ta có \(I=\int\limits_{0}^{1}{{{e}^{x\,+\,1}}\,\text{d}x}=\,\int\limits_{0}^{1}{{{e}^{x\,+\,1}}\,\text{d}\left( x+1 \right)}=\left. {{e}^{x\,+\,1}} \right|_{0}^{1}={{e}^{2}}-e.\)
Chọn B
Câu hỏi 20 :
Tích phân \(\int\limits_{1}^{2}{{{\left( x+3 \right)}^{2}}dx}\) bằng
- A \(61.\)
- B \(\frac{61}{3}.\)
- C \(4.\)
- D \(\frac{61}{9}.\)
Đáp án: B
Câu hỏi 21 :
Tích phân \(\int\limits_0^1 {x\left( {{x^2} + 3} \right)\,{\rm{d}}x} \) bằng
- A 2.
- B \(\frac{7}{4}.\)
- C \(\frac{4}{7}.\)
- D 1.
Đáp án: B
Câu hỏi 22 :
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\) và \(\int\limits_0^1 {g\left( x \right)dx} = 5\), khi đó \(\int\limits_0^1 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]dx} \) bằng
- A \( - 3\)
- B \(12\)
- C \( - 8\)
- D \(1\)
Đáp án: C
Phương pháp giải:
Sử dụng tính chất tích phân \(\int\limits_a^b {\left[ {\alpha f\left( x \right) \pm \beta g\left( x \right)} \right]dx} = \alpha \int\limits_a^b {f\left( x \right)dx} \pm \beta \int\limits_a^b {g\left( x \right)dx} \)
Lời giải chi tiết:
Ta có: \(\int\limits_0^1 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]dx} = \int\limits_0^1 {f\left( x \right)dx} - 2\int\limits_0^1 {g\left( x \right)dx} = 2 - 2.5 = - 8\)
CHỌN C
Câu hỏi 23 :
Cho \(f\left( x \right),g\left( x \right)\) là hai hàm số liên tục trên \(\mathbb{R}\). Chọn mệnh đề sai trong các mệnh đề sau
- A \(\int\limits_a^b {\left( {f\left( x \right).g\left( x \right)} \right)dx} = \int\limits_a^b {f\left( x \right)dx.\int\limits_a^b {g\left( x \right)dx} } \)
- B \(\int\limits_a^a {f\left( x \right)dx = 0} \)
- C \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^b {f\left( y \right)dy} \)
- D \(\int\limits_a^b {\left( {f\left( x \right) - g\left( x \right)} \right)dx} = \int\limits_a^b {f\left( x \right)dx - \int\limits_a^b {g\left( x \right)dx} } \)
Đáp án: A
Phương pháp giải:
Sử dụng tính chất tích phân.
Lời giải chi tiết:
Ta có
\(\left\{ \begin{array}{l}\int\limits_a^a {f\left( x \right)dx = 0} ;\,\,\,\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^b {f\left( y \right)dy} ;\\\int\limits_a^b {\left( {f\left( x \right) - g\left( x \right)} \right)dx} = \int\limits_a^b {f\left( x \right)dx - \int\limits_a^b {g\left( x \right)dx} } \end{array} \right.\) nên B, C, D đúng.
A sai vì tích phân một tích không bằng tích các tích phân.
Chọn A.
Câu hỏi 24 :
Cho hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và số thực \(k\) tùy ý. Trong các khẳng định sau, khẳng định nào sai?
- A \(\int\limits_a^a {kf\left( x \right)dx} = 0\)
- B \(\int\limits_a^b {xf\left( x \right)dx} = x\int\limits_a^b {f\left( x \right)dx} \)
- C \(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} \)
- D \(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \).
Đáp án: B
Phương pháp giải:
Sử dụng các tính chất của tích phân:
\(\int\limits_a^a {kf\left( x \right)dx} = 0\)
\(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} \)
\(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \)
Lời giải chi tiết:
Dựa vào các đáp án ta dễ dàng nhận thấy các đáp án A, C, D đúng, đáp án B sai.
Chọn B.
Câu hỏi 25 :
Cho \(\int\limits_1^2 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {2g\left( x \right)dx} = 8\). Khi đó \(\int\limits_1^2 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} \) bằng:
- A 10
- B 6
- C 18
- D 0
Đáp án: B
Phương pháp giải:
Sử dụng tính chất tích phân: \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} = \int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} \).
Lời giải chi tiết:
Ta có: \(\int\limits_1^2 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int\limits_1^2 {f\left( x \right)dx} + \int\limits_1^2 {g\left( x \right)dx} = 2 + 4 = 6\).
Chọn B.
Câu hỏi 26 :
Cho các hàm số \(f\left( x \right)\) và \(F\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa \(F'\left( x \right) = f\left( x \right),\forall x \in \mathbb{R}\). Tính \(\int\limits_0^1 {f\left( x \right)dx} \) biết \(F\left( 0 \right) = 2,\,F\left( 1 \right) = 5\).
- A \(\int\limits_0^1 {f\left( x \right)dx} = 7\).
- B \(\int\limits_0^1 {f\left( x \right)dx} = 1\).
- C \(\int\limits_0^1 {f\left( x \right)dx} = 3\).
- D \(\int\limits_0^1 {f\left( x \right)dx} = - 3\).
Đáp án: C
Phương pháp giải:
Sử dụng công thức \(\int\limits_a^b {F'\left( x \right)dx} = F\left( b \right) - F\left( a \right)\).
Lời giải chi tiết:
Ta có: \(\int\limits_0^1 {f\left( x \right)dx} = \int\limits_0^1 {F'\left( x \right)dx} = F\left( 1 \right) - F\left( 0 \right) = 5 - 2 = 3\).
Chọn: C
Câu hỏi 27 :
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và a là số dương. Trong các khẳng định sau, khẳng định nào đúng?
- A \(\int\limits_a^a {f\left( x \right)dx} = 0\).
- B \(\int\limits_a^a {f\left( x \right)dx} = {a^2}\).
- C \(\int\limits_a^a {f\left( x \right)dx} = 2a\).
- D \(\int\limits_a^a {f\left( x \right)dx} = 1\).
Đáp án: A
Phương pháp giải:
Sử dụng tính chất của tích phân: \(\int\limits_a^a {f\left( x \right)dx} = 0\)
Lời giải chi tiết:
\(\int\limits_a^a {f\left( x \right)dx} = 0\).
Chọn: A
Câu hỏi 28 :
Để tính tích phân \(I = \int\limits_0^{\dfrac{\pi }{2}} {{e^{\sin x}}\cos xdx} \) ta chọn cách đặt nào sau đây cho phù hợp ?
- A Đặt \(t = {e^{\cos x}}\)
- B Đặt \(t = {e^x}\)
- C Đặt \(t = \cos x\)
- D Đặt \(t = \sin x\)
Đáp án: D
Phương pháp giải:
Tính tích phân bằng phương pháp đặt ẩn phụ.
Lời giải chi tiết:
Đặt \(t = \sin x \Rightarrow dt = \cos xdx\). Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = \dfrac{\pi }{2} \Rightarrow t = 1\end{array} \right.\).
Ta có: \(I = \int\limits_0^{\dfrac{\pi }{2}} {{e^{\sin x}}\cos xdx} = \int\limits_0^1 {{e^t}dt} = \left. {{e^t}} \right|_0^1 = e - 1\).
Chọn D.
Câu hỏi 29 :
Giá trị của \(\int\limits_0^1 {\pi x{e^x}dx} \) là:
- A \(\pi \)
- B \(\pi e\)
- C \(\dfrac{\pi }{3}\)
- D \(\dfrac{1}{3}\)
Đáp án: A
Phương pháp giải:
Sử dụng MTCT.
Lời giải chi tiết:
Sử dụng MTCT ta có:
Chọn A.
Câu hỏi 30 :
Tính tích phân \(I = \int\limits_1^e {\dfrac{{3\ln x + 1}}{x}{\rm{d}}x} \). Nếu đặt \(t = \ln x\) thì
- A
\(I = \int\limits_0^1 {\dfrac{{3t + 1}}{{{e^t}}}{\rm{d}}t} \)
- B \(I = \int\limits_1^e {\dfrac{{3t + 1}}{t}{\rm{d}}t} \)
- C \(I = \int\limits_1^e {\left( {3t + 1} \right){\rm{d}}t} \)
- D \(I = \int\limits_0^1 {\left( {3t + 1} \right){\rm{d}}t} \)
Đáp án: D
Phương pháp giải:
Tính \(dt\), đổi cận và thay vào tính \(I\).
Lời giải chi tiết:
Đặt \(t = \ln x\)\( \Rightarrow {\rm{d}}t = \dfrac{{{\rm{d}}x}}{x}\). Đổi cận: \(x = 1 \Rightarrow t = 0;x = e \Rightarrow t = 1\)
Vậy \(I = \int\limits_0^1 {\left( {3t + 1} \right){\rm{d}}t} \)
Chọn D.
Câu hỏi 31 :
Khẳng định nào dưới đây là đúng?
- A \(\int\limits_{ - 2}^2 {f\left( x \right)dx} = - \int\limits_0^2 {\left[ {f\left( x \right) + f\left( { - x} \right)} \right]dx} \)
- B \(\int\limits_{ - 2}^2 {f\left( x \right)dx} = - 2\int\limits_0^2 {f\left( x \right)dx} \)
- C \(\int\limits_{ - 2}^2 {2f\left( x \right)dx} = 2\int\limits_{ - 2}^2 {f\left( x \right)dx} \)
- D \(\int\limits_{ - 2}^2 {f\left( x \right)dx} = 2\int\limits_0^2 {f\left( x \right)dx} \)
Đáp án: C
Phương pháp giải:
Sử dụng các tính chất: \(\int\limits_{}^{} {kf\left( x \right)dx} = k\int\limits_{}^{} {f\left( x \right)dx} \).
Lời giải chi tiết:
Khẳng định đúng là \(\int\limits_{ - 2}^2 {2f\left( x \right)dx} = 2\int\limits_{ - 2}^2 {f\left( x \right)dx} \).
Chọn C.
Câu hỏi 32 :
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_0^4 {f\left( x \right)dx} = 10,\,\,\int\limits_3^4 {f\left( x \right)dx} = 4\). Tích phân \(\int\limits_0^3 {f\left( x \right)dx} \) bằng:
- A 4
- B 7
- C 3
- D 6
Đáp án: D
Phương pháp giải:
Sử dụng tính chất của tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \).
Lời giải chi tiết:
\(\int\limits_0^3 {f(x)dx} \)\( = \int\limits_0^4 {f\left( x \right)} dx + \int\limits_4^3 {f\left( x \right)} dx = \int\limits_0^4 {f\left( x \right)} dx - \int\limits_3^4 {f\left( x \right)} dx\)\( = 10 - 4 = 6\).
Chọn: D
Câu hỏi 33 :
Với \(f\left( x \right)\) là hàm số tùy ý liên tục trên \(\mathbb{R},\) chọn mệnh đề sai trong các mệnh đề sau:
- A \({\left( {\int\limits_a^b {f\left( x \right)dx} } \right)^2} = \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} \)
- B \(\int\limits_a^b {kf\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} \,\,\,\left( {k \in \mathbb{R}} \right)\)
- C \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \)
- D \(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \)
Đáp án: A
Phương pháp giải:
Sử dụng các tính chất cơ bản của tích phân để chọn đáp án đúng:
\(\begin{array}{l}\int\limits_a^b {kf\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} \,\,\,\left( {k \in \mathbb{R}} \right)\\\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \\\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \end{array}\)
Lời giải chi tiết:
Sử dụng các tính chất cơ bản của tích phân ta thấy chỉ có đáp án A sai.
Chọn A.
Câu hỏi 34 :
Cho hàm số \(f\left( x \right)\) thỏa mãn \(\int\limits_1^3 {f\left( x \right)dx} = 5\) và \(\int\limits_{ - 1}^3 {f\left( x \right)dx} = 1\). Tính tích phân \(I = \int\limits_{ - 1}^1 {f\left( x \right)dx} \).
- A \(I = - 4\).
- B \(I = - 6\).
- C \(I = 6\).
- D \(I = 4\).
Đáp án: A
Phương pháp giải:
Sử dụng tính chất tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \).
Lời giải chi tiết:
\(I = \int\limits_{ - 1}^1 {f\left( x \right)dx} = \int\limits_{ - 1}^3 {f\left( x \right)dx} + \int\limits_3^1 {f\left( x \right)dx} = \int\limits_{ - 1}^3 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} = 1 - 5 = - 4\).
Chọn: A
Câu hỏi 35 :
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 3\) và \(\int\limits_1^2 {f\left( x \right)dx = 2.} \) Khi đó \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
- A \(1\)
- B \( - 1\)
- C \(5\)
- D \(6\)
Đáp án: C
Phương pháp giải:
Sử dụng tính chất tích phân: \(\int\limits_a^b {f\left( x \right)dx + } \int\limits_b^c {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} \)
Lời giải chi tiết:
Ta có \(\int\limits_0^1 {f\left( x \right)dx + } \int\limits_1^2 {f\left( x \right)dx} = \int\limits_0^2 {f\left( x \right)dx} \Leftrightarrow \int\limits_0^2 {f\left( x \right)dx} = 2 + 3 = 5.\)
Chọn C.
Câu hỏi 36 :
Giả sử \(f\left( x \right)\) và \(g\left( x \right)\) là các số bất kì liên tục trên \(\mathbb{R}\) và \(a,\,b,\,c\) là các số thực. Mệnh dề nào sau đây sai?
- A \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} + \int\limits_c^a {f\left( x \right)dx} = 0\)
- B \(\int\limits_a^b {cf\left( x \right)dx} = c\int\limits_a^b {f\left( x \right)dx} \)
- C \(\int\limits_a^b {f\left( x \right).g\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx + } \int\limits_a^b {g\left( x \right)dx} \)
- D \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} + \int\limits_a^b {g\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx} \)
Đáp án: C
Phương pháp giải:
Sử dụng các tính chất cơ bản của tích phân để chọn đáp án đúng:
\(\begin{array}{l}\int\limits_a^b {kf\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} \,\,\,\left( {k \in \mathbb{R}} \right)\\\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \\\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \end{array}\)
Lời giải chi tiết:
Dựa vào các tính chất cơ bản của tích phân ta có:
\(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} + \int\limits_c^a {f\left( x \right)dx} = \int\limits_a^a {f\left( x \right)dx} = 0 \Rightarrow \) đáp án A đúng.
\(\int\limits_a^b {cf\left( x \right)dx} = c\int\limits_a^b {f\left( x \right)dx} \Rightarrow \) đáp án B đúng.
\(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} + \int\limits_a^b {g\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx} \Rightarrow \)đáp án D đúng.
Chọn C.
Câu hỏi 37 :
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) liên tục liên tục trên đoạn \(\left[ {a;b} \right]\). Biết \(f\left( a \right) = 5\) và \(\int\limits_a^b {f'\left( x \right)dx} = 2\sqrt 5 \), tính \(f\left( b \right)\).
- A \(\sqrt 5 \left( {2 - \sqrt 5 } \right)\)
- B \(\sqrt 5 \left( {\sqrt 5 + 2} \right)\)
- C \(\sqrt 2 \left( {\sqrt 5 - 2} \right)\)
- D \(\sqrt 5 \left( {\sqrt 5 - 2} \right)\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tích phân \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\).
Lời giải chi tiết:
Ta có: \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\)\( \Rightarrow f\left( b \right) - f\left( a \right) = 2\sqrt 5 \)
\( \Rightarrow f\left( b \right) - 5 = 2\sqrt 5 \) \( \Leftrightarrow f\left( b \right) = 5 + 2\sqrt 5 = \sqrt 5 \left( {\sqrt 5 + 2} \right)\)
Chọn B.
Câu hỏi 38 :
Tính \(I = \int\limits_{ - 1}^2 {6{x^2}dx} \).
- A \(I = 18\).
- B \(I = 22\).
- C \(I = 26\)
- D \(I = 14\).
Đáp án: A
Phương pháp giải:
Sử dụng công thức: \(\int\limits_a^b {{x^n}dx} = \left. {\dfrac{{{x^{n + 1}}}}{{n + 1}}} \right|_a^b,\,\,\left( {n \ne - 1} \right)\).
Lời giải chi tiết:
Ta có: \(I = \int\limits_{ - 1}^2 {6{x^2}dx} = \left. {2{x^3}} \right|_{ - 1}^2 = 16 + 2 = 18\).
Chọn: A
Câu hỏi 39 :
Tính \(I = \int\limits_0^1 {{e^x}} dx\).
- A \(I = {e^2} - e\).
- B \(I = e - 1\).
- C \(I = 1 - e\).
- D \(I = e\).
Đáp án: B
Phương pháp giải:
Sử dụng công thức nguyên hàm cơ bản.
Lời giải chi tiết:
\(I = \int\limits_0^1 {{e^x}} dx = \left. {{e^x}} \right|_0^1 = e - 1\)
Chọn: B
Câu hỏi 40 :
Cho \(\int\limits_1^5 {f\left( x \right)} dx = a\) và \(\int\limits_1^{2018} {f\left( x \right)} dx = b\). Khi đó \(\int\limits_5^{2018} {f\left( x \right)} dx\) bằng
- A \(b - a\).
- B \( - a - b\).
- C \(a - b\).
- D \(a + b\).
Đáp án: A
Phương pháp giải:
Sử dụng tính chất tích phân: \(\int\limits_a^b {f\left( x \right)} dx = \int\limits_a^c {f\left( x \right)} dx + \int\limits_c^b {f\left( x \right)} dx\).
Lời giải chi tiết:
Ta có: \(\int\limits_5^{2018} {f\left( x \right)} dx = \int\limits_5^1 {f\left( x \right)} dx + \int\limits_1^{2018} {f\left( x \right)} dx = - \int\limits_1^5 {f\left( x \right)} dx + \int\limits_1^{2018} {f\left( x \right)} dx = - a + b\).
Chọn: A
Câu hỏi 41 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên đoạn \(\left[ { - 2;1} \right]\) và \(f\left( { - 2} \right) = 3,\,f\left( 1 \right) = 7\). Tính \(I = \int\limits_{ - 2}^1 {f'\left( x \right)dx} \).
- A \(I = 10\).
- B \(I = - 4\).
- C \(I = \dfrac{7}{3}\).
- D \(I = 4\)
Đáp án: D
Phương pháp giải:
\(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) \Rightarrow \int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\).
Lời giải chi tiết:
\(I = \int\limits_{ - 2}^1 {f'\left( x \right)dx} = f\left( 1 \right) - f\left( { - 2} \right) = 7 - 3 = 4\).
Chọn: D
Câu hỏi 42 :
Giả sử \(\int\limits_a^b {f\left( x \right)dx} = 2,\,\,\int\limits_c^b {f\left( x \right)dx} = 3\) với \(a < b < c\) thì \(\int\limits_a^c {f\left( x \right)dx} \) bằng:
- A \(5\)
- B 1
- C -2
- D -1.
Đáp án: D
Phương pháp giải:
\(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \)
Lời giải chi tiết:
\(\int\limits_a^c {f\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_c^b {f\left( x \right)dx} = 2 - 3 = - 1\).
Chọn: D
Câu hỏi 43 :
Cho hai hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(a < c < b\). Mệnh đề nào dưới đây sai?
- A \(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx = \int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} } \)
- B \(\int\limits_a^b {k.f\left( x \right)dx = } k.\int\limits_a^b {f\left( x \right)dx} \)với \(k\) là hằng số
- C \(\int\limits_a^b {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}dx} = \dfrac{{\int\limits_a^b {f\left( x \right)dx} }}{{\int\limits_a^b {g\left( x \right)dx} }}\)
- D \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \)
Đáp án: C
Phương pháp giải:
Sử dụng tính chất của tích phân.
Lời giải chi tiết:
Dễ thấy A, B, D đúng.
C sai: \(\int\limits_a^b {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}dx} \ne \dfrac{{\int\limits_a^b {f\left( x \right)dx} }}{{\int\limits_a^b {g\left( x \right)dx} }}\)
Chọn C
Câu hỏi 44 :
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\). Mệnh đề nào dưới đây đúng?
- A \(\int\limits_a^b {f\left( x \right)dx} = F\left( a \right) - F\left( b \right)\)
- B \(\int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\)
- C \(\int\limits_a^b {f\left( x \right)dx} = F\left( b \right) + F\left( a \right)\)
- D \(\int\limits_a^b {f\left( x \right)dx} = F'\left( b \right) - F'\left( a \right)\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tích phân Leibnitz: \(\int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\) với \(F'\left( x \right) = f\left( x \right)\).
Lời giải chi tiết:
Do \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) nên \(\int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\).
Chọn B
Câu hỏi 45 :
Cho \(f\left( x \right)\) và \(g\left( x \right)\) là các hàm số liên tục bất kì trên đoạn \(\left[ {a;\,\,b} \right].\) Mênh đề nào sau đây đúng?
- A \(\int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
- B \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
- C \(\left| {\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} } \right|dx = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} \)
- D \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \left| {\int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} } \right|\)
Đáp án: B
Phương pháp giải:
Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} .\)
Lời giải chi tiết:
Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} .\)
Chọn B.
Câu hỏi 46 :
Cho các số thực a, b \((a<b)\). Nếu hàm số \(y=f(x)\) có đạo hàm là hàm liên tục trên \(\mathbb{R}\) thì
- A \(\int\limits_a^b {f\left( x \right)dx} = f'\left( a \right) - f'\left( b \right)\)
- B \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\)
- C \(\int\limits_a^b {f'\left( x \right)dx} = f\left( a \right) - f\left( b \right)\)
- D \(\int\limits_a^b {f\left( x \right)dx} = f'\left( b \right) - f'\left( a \right)\)
Đáp án: B
Lời giải chi tiết:
Chọn B.
Câu hỏi 47 :
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( 0 \right) = 1,f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_0^3 {f'\left( x \right)dx} = 9\). Giá trị của \(f\left( 3 \right)\) là
- A 6
- B 3
- C 10
- D 9
Đáp án: C
Phương pháp giải:
Sử dụng công thức tích phân \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\).
Lời giải chi tiết:
Ta có: \(\int\limits_0^3 {f'\left( x \right)dx} = 9 = f\left( 3 \right) - f\left( 0 \right)\)\( \Rightarrow f\left( 3 \right) = 9 + f\left( 0 \right) = 9 + 1 = 10\).
Chọn C.
Câu hỏi 48 :
Cho hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và số thực \(k\) tùy ý. Trong các phát biểu sau, phát biểu nào sai?
- A \(\int\limits_a^b {f\left( x \right){\rm{d}}x} = - \int\limits_b^a {f\left( x \right){\rm{d}}x} \).
- B \(\int\limits_a^a {kf\left( x \right){\rm{d}}x} = 0\).
- C \(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]{\rm{d}}x} = \int\limits_a^b {f\left( x \right){\rm{d}}x} + \int\limits_a^b {g\left( x \right){\rm{d}}x} \).
- D \(\int\limits_a^b {xf\left( x \right){\rm{d}}x} = x\int\limits_a^b {f\left( x \right){\rm{d}}x} \).
Đáp án: D
Phương pháp giải:
Sử dụng các tính chất của tích phân.
Lời giải chi tiết:
Dễ thấy mệnh đề sai là: \(\int\limits_a^b {xf\left( x \right){\rm{d}}x} = x\int\limits_a^b {f\left( x \right){\rm{d}}x} \).
Chọn D.
Câu hỏi 49 :
Cho các hàm số \(f\left( x \right),\,\,\,g\left( x \right)\) liên tục trên tập xác định. Tìm mệnh đề sai?
- A \(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int {f\left( x \right)dx + \int {g\left( x \right)dx} } \)
- B \(\int {f'\left( x \right)dx} = f\left( x \right) + C\)
- C \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} ,\,\,\,\forall k \in \mathbb{R}\)
- D \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Đáp án: C
Phương pháp giải:
Dựa vào tính chất tích phân.
Lời giải chi tiết:
Mệnh đề sai là C. Mệnh đề đúng phải là: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \,\,\forall k \in \mathbb{R},\,\,k \ne 0\).
Chọn C.
Câu hỏi 50 :
Tính tích phân \(I = \int\limits_0^1 {\left| {x - 2} \right|dx} \) ta được kết quả:
- A \(\dfrac{1}{2}\)
- B \(1\)
- C \(\dfrac{3}{2}\)
- D \(2\)
Đáp án: C
Phương pháp giải:
- Xét dấu của biểu thức \(x - 2\) trên \(\left[ {0;1} \right]\) và phá trị tuyệt đối.
- Sử dụng các nguyên hàm cơ bản để tính tích phân.
Lời giải chi tiết:
Với \(x \in \left[ {0;1} \right]\) thì \(x - 2 < 0\), do đó \(\left| {x - 2} \right| = 2 - x\).
Khi đó ta có: \(I = \int\limits_0^1 {\left| {x - 2} \right|dx} = \int\limits_0^1 {\left( {2 - x} \right)dx} \)\( = \left. {\left( {2x - \dfrac{{{x^2}}}{2}} \right)} \right|_0^1 = 2 - \dfrac{1}{2} = \dfrac{3}{2}\).
Chọn C.
Tổng hợp các bài tập trắc nghiệm nguyên tích phân độ vận dụng, vận dụng cao có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm nguyên tích phân độ nhận biết, thông hiểu có đáp án và lời giải chi tiết
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục