50 bài tập các phép toán với số phức mức độ nhận biết, thông hiểu
Làm đề thiCâu hỏi 1 :
Tìm số phức thỏa mãn: \((1+3i)z-(2+5i)=(2+i)z\)
- A \(z=\frac{8}{5}-\frac{9}{5}i\)
- B \(z=\frac{8}{5}+\frac{9}{5}i\)
- C \(z=-\frac{8}{5}-\frac{9}{5}i\)
- D \(z=-\frac{8}{5}+\frac{9}{5}i\)
Đáp án: A
Phương pháp giải:
Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm \(a,b\Rightarrow z\).
Lưu ý: phương pháp đồng nhất hệ số \(a+bi=a'+b'i\Leftrightarrow a=a';b=b'\).
Lời giải chi tiết:
Giả sử \(z=a+bi\left( a,b\in R \right)\)
\(\begin{array}{l}(1 + 3i)z - (2 + 5i) = (2 + i)z\\ \Leftrightarrow \left( {1 + 3i - 2 - i} \right)z = 2 + 5i\\ \Leftrightarrow \left( { - 1 + 2i} \right)(a + bi) = 2 + 5i\\ \Leftrightarrow - a - bi + 2ai - 2b = 2 + 5i\\ \Leftrightarrow \left\{ \begin{array}{l} - a - 2b = 2\\2a - b = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{8}{5}\\b = - \frac{9}{5}\end{array} \right.\\ \Rightarrow z = \frac{8}{5} - \frac{9}{5}i\end{array}\)
Chọn A
Câu hỏi 2 :
Số phức thỏa mãn: \((3+4i)z+(1-3i)=2+5i\) là:
- A \(z=-\frac{7}{5}+\frac{4}{5}i\)
- B \(z=\frac{7}{5}+\frac{4}{5}i\)
- C \(z=-\frac{7}{5}-\frac{4}{5}i\)
- D \(z=\frac{7}{5}-\frac{4}{5}i\)
Đáp án: B
Phương pháp giải:
Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm \(a,b\Rightarrow z\).
Lưu ý: phương pháp đồng nhất hệ số \(a+bi=a'+b'i\Leftrightarrow a=a';b=b'\).
Lời giải chi tiết:
Giả sử \(z=a+bi\left( a,b\in R \right)\), ta có:
\(\begin{array}{l}(3 + 4i)z + (1 - 3i) = 2 + 5i\\ \Leftrightarrow (3 + 4i)z = 1 + 8i\\ \Leftrightarrow (3 + 4i)(a + bi) = 1 + 8i\\ \Leftrightarrow 3a + 3bi + 4ai - 4b = 1 + 8i\\ \Leftrightarrow \left\{ \begin{array}{l}3a - 4b = 1\\4a + 3b = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{7}{5}\\b = \frac{4}{5}\end{array} \right.\\ \Rightarrow z = \frac{7}{5} + \frac{4}{5}i\end{array}\)
Chọn B
Câu hỏi 3 :
Số phức \(z\) thỏa mãn: \((3-2i)\overline{z}-4(1-i)=(2+i)z\). Mô đun của z là:
- A \(\sqrt{3}\)
- B \(\sqrt{5}\)
- C \(\sqrt{10}\)
- D \(\frac{\sqrt{3}}{4}\)
Đáp án: C
Phương pháp giải:
Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm \(a,b\Rightarrow z\).
Tính mô đun của \(z:\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\).
Lưu ý: phương pháp đồng nhất hệ số \(a+bi=a'+b'i\Leftrightarrow a=a';b=b'\).
Lời giải chi tiết:
Giả sử \(z=a+bi\left( a,b\in R \right)\), ta có:
\(\begin{array}{l}\Rightarrow (3 - 2i)(a - bi) - 4(1 - i) = (2 + i)(a + bi)\\\Leftrightarrow 3a - 3bi - 2ai - 2b - 4 + 4i = 2a + 2bi + ai - b\\\Leftrightarrow \left\{ \begin{array}{l}3a - 2b - 4 = 2a - b\\- 2a - 3b + 4 = a + 2b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b = 4\\3a + 5b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 1\end{array} \right.\\ \Rightarrow z = 3 - i \Rightarrow \left| z \right| = \sqrt {10} \end{array}\)
Chọn C
Câu hỏi 4 :
Điểm biểu diễn số phức thỏa mãn \((3+2i)z=5-14i\) có tọa độ là:
- A \(\left( -1;-4 \right)\)
- B \(\left( 1;-4 \right)\)
- C \(\left( -1;4 \right)\)
- D \(\left( -4;-1 \right)\)
Đáp án: A
Phương pháp giải:
Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm .
Lưu ý: phương pháp đồng nhất hệ số \(a+bi=a'+b'i\Leftrightarrow a=a';b=b'\).
Điểm biểu diễn số phức \(z=a+bi\) là điểm \(M\left( a;b \right)\).
Lời giải chi tiết:
Giả sử \(z=a+bi\left( a,b\in R \right)\), ta có:
\(\begin{array}{l} \Rightarrow (3 + 2i)(a + bi) = 5 - 14i\\ \Leftrightarrow 3a + 3bi + 2ai - 2b = 5 - 14i\\ \Leftrightarrow \left\{ \begin{array}{l}3a - 2b = 5\\2a + 3b = - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = - 4\end{array} \right.\end{array}\)
Þ Điểm biểu diễn của có tọa độ là: \((-1;-4)\)
Chọn A
Câu hỏi 5 :
Cho số phức z = a + bi \((a, b \in R)\) thỏa mãn: \((1+i)z+2\overline{z}=3+2i\). Tính \(P=a+b\)
- A \(P=\frac{1}{2}\)
- B \(P=1\)
- C \(P=-1\)
- D \(P=-\frac{1}{2}\)
Đáp án: C
Phương pháp giải:
Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm \(a,b\Rightarrow P\).
Lưu ý: phương pháp đồng nhất hệ số \(a+bi=a'+b'i\Leftrightarrow a=a';b=b'\).
Lời giải chi tiết:
Giả sử \(z=a+bi\left( a,b\in R \right)\), ta có:
\(\begin{array}{l}(1 + i)z + 2\overline z = 3 + 2i\\ \Leftrightarrow (1 + i)(a + bi) + 2(a - bi) = 3 + 2i\\ \Leftrightarrow a + ai + bi - b + 2a - 2bi = 3 + 2i\\ \Leftrightarrow \left\{ \begin{array}{l}3a - b = 3\\a - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = - \frac{3}{2}\end{array} \right.\\ \Rightarrow P = \frac{1}{2} - \frac{3}{2} = - 1\end{array}\)
Chọn C
Câu hỏi 6 :
Mô đun của số phức \(z=5+2i-{{\left( 1+i \right)}^{3}}\) là:
- A 7
- B 3
- C 5
- D 2
Đáp án: A
Phương pháp giải:
- Rút gọn số phức \(z=a+bi\).
- Tính mô đun \(\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\).
Lời giải chi tiết:
Ta có: \(z=5+2i-{{\left( 1+i \right)}^{3}}=5+2i-(1+3i+3{{i}^{2}}+{{i}^{3}})\)
\(=5+2i+2-2i=7\)
\(\Rightarrow \left| z \right|=\sqrt{49}=7\)
Chọn A
Câu hỏi 7 :
Thu gọn \(z={{\left( \sqrt{2}+3i \right)}^{2}}\) ta được:
- A \(z=11-6i\)
- B \(z=-1-i\)
- C \(z=4+3i\)
- D \(z=-7+6\sqrt{2}i\)
Đáp án: D
Phương pháp giải:
Dùng hằng đẳng thức \({{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\) với chú ý \({{i}^{2}}=-1\).
Lời giải chi tiết:
Ta có: \(z={{\left( \sqrt{2}+3i \right)}^{2}}=2+6\sqrt{2}i+9{{i}^{2}}=-7+6\sqrt{2}i\)
Chọn D
Câu hỏi 8 :
Rút gọn biểu thức \(z=i\left( 2-i \right)\left( 3+i \right)\) ta được:
- A \(z=6\)
- B \(z=1+7i\)
- C \(z=2+5i\)
- D \(z=5i\)
Đáp án: B
Phương pháp giải:
- Dùng quy tắc nhân hai số phức.
Lời giải chi tiết:
Ta có: z = i(2 – i)(3 + i) =\(\left( 2i+1 \right)\left( 3+i \right)\)
\(=6i+2{{i}^{2}}+3+i=1+7i\)
Chọn B
Câu hỏi 9 :
Phần ảo của số phức \(z={{\left( \sqrt{2}+i \right)}^{2}}\left( 1-\sqrt{2}i \right)\) là:
- A \(-\sqrt{2}\)
- B \(2\)
- C \(\sqrt{2}\)
- D \(3\)
Đáp án: C
Phương pháp giải:
- Rút gọn số phức \(z=a+bi\).
- Phần ảo của số phức \(z=a+bi\) là \(b\).
Lời giải chi tiết:
Ta có: \(z={{\left( \sqrt{2}+i \right)}^{2}}\left( 1-\sqrt{2}i \right)=\left( 2+2\sqrt{2}i+{{i}^{2}} \right)\left( 1-\sqrt{2}i \right)\)
\(=\left( 1+2\sqrt{2}i \right)\left( 1-\sqrt{2}i \right)=1-\sqrt{2}i+2\sqrt{2}i-4{{i}^{2}}=5+\sqrt{2}i\)
Phần ảo của số phức \(z\) là \(\sqrt{2}\)
Chọn C
Câu hỏi 10 :
Gọi \(M\left( x;\ y \right)\) là điểm biểu diễn số phức \(z=\left( 6+7i \right)i\) trong mặt phẳng phức. Tìm tọa độ điểm M.
- A \(M\left( 6;\ 7 \right)\)
- B \(M\left( -6;-7 \right)\)
- C \(M\left( 6;-7 \right)\)
- D \(M\left( -7;\ 6 \right)\)
Đáp án: D
Phương pháp giải:
+) Cho số phức \(z=a+bi\ \ \left( a;\ b\in R \right)\) thì điểm \(M\left( a;\ b \right)\) biểu diễn số phức z.
Lời giải chi tiết:
Ta có: \(z=\left( 6+7i \right)i=6i+7{{i}^{2}}=-7+6i.\)
\(\Rightarrow M\left( -7;\ 6 \right)\) là điểm biểu diễn số phức z.
Chọn D.
Câu hỏi 11 :
Cho hai số phức \(z=2+3i,z'=3-2i\). Tìm môđun của số phức \(w=z.z'\).
- A \(\left| w \right|=\sqrt{13}\)
- B \(\left| w \right|=13\)
- C \(\left| w \right|=12\)
- D \(\left| w \right|=14\)
Đáp án: B
Phương pháp giải:
Tính \(z.z'\Rightarrow w\)
Tính môđun của số phức \(w=a+bi\): \(\left| w \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\)
Lời giải chi tiết:
Sử dụng MTCT ta tính được:
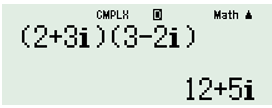
\(\Rightarrow \left| w \right|=\sqrt{{{12}^{2}}+{{5}^{2}}}=13\).
Chọn B.
Câu hỏi 12 :
Cho hai số phức \({{z}_{1}}=1+2i;\)\({{z}_{2}}=2-3i\). Xác định phần ảo của số phức \(3{{z}_{1}}-2{{z}_{2}}\)
- A \(11\)
- B \(12\)
- C \(10\)
- D \(13\)
Đáp án: B
Phương pháp giải:
- Tính số phức \(3{{z}_{1}}-2{{z}_{2}}\)
- Phần ảo của số phức \(z=a+bi\) là \(b\).
Lời giải chi tiết:
Ta có: \(3{{z}_{1}}-2{{z}_{2}}=3(1+2i)-2(2-3i)=3+6i-4+6i=-1+12i\)
=> Phần ảo của nó là \(12\)
Chọn B
Câu hỏi 13 :
Cho số phức \(z=3-2i.\) Tìm số phức \(w=i.\bar{z}-z.\)
- A \(w=-\,5+5i.\)
- B \(w=-\,1+5i.\).
- C \(w=-\,5+i.\)
- D \(w=5-5i.\)
Đáp án: A
Phương pháp giải:
Xác định số phức liên hợp và tìm số phức w bằng máy tính casio.
Lời giải chi tiết:
Ta có \(z=3-2i\Rightarrow \bar{z}=3+2i\Rightarrow i.\bar{z}=-\,2+3i.\)
Vậy \(w=i.\bar{z}-z=-\,2+3i-3+2i=-\,5+5i.\)
Chọn A
Câu hỏi 14 :
Cho số phức \(z=(1+2i)(5-i)\), \(z\) có phần thực là
- A 5
- B 7
- C 3
- D 9
Đáp án: B
Phương pháp giải:
Số phức \(z=a+bi,\,\,\left( a,\,b\in \mathbb{R} \right)\)có phần thực là a, phần ảo là b.
Lời giải chi tiết:
\(z=\left( 1+2i \right)\left( 5-i \right)=5-i+10i-2{{i}^{2}}=5-i+10i+2=7+9i\)
\(z\)có phần thực là 7.
Chọn: B
Câu hỏi 15 :
Cho số phức \(z = \left( {3 - 2i} \right){\left( {1 + i} \right)^2}\). Môđun của \(w = iz + \overline z \) là
- A \(8\)
- B \(2\sqrt 2 \)
- C \(1\)
- D \(\sqrt 2 \)
Đáp án: B
Phương pháp giải:
- Tìm số phức z rồi suy ra số phức w.
- Môđun của số phức \(w = a + bi\) là \(\left| w \right| = \sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết:
Ta có \(z = \left( {3 - 2i} \right){\left( {1 + i} \right)^2} = 4 + 6i\)
Khi đó ta có:
\(\begin{array}{l}w = iz + \overline z = i\left( {4 + 6i} \right) + \left( {4 - 6i} \right) = - 2 - 2i\\ \Rightarrow \left| w \right| = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 .\end{array}\)
Chọn B.
Câu hỏi 16 :
Phần ảo của số phức \(z = i{\left( {1 + 2i} \right)^2}\)là:
- A \(3\)
- B \( - 5\)
- C \( - 3\)
- D \(5\)
Đáp án: C
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right).\) Khi đó \(a\) là phần thực, \(b\) là phần ảo của số phức \(z.\)
Lời giải chi tiết:
Ta có: \(z = i{\left( {1 + 2i} \right)^2}\)\( = i\left( {1 + 4i + 4{i^2}} \right)\) \( = i\left( {4i - 3} \right)\)\( = 4{i^2} - 3i = - 4 - 3i\)
\( \Rightarrow \) Phần ảo của số phức \(z\) là \( - 3.\)
Chọn C.
Câu hỏi 17 :
Cho số phức \(z\) thỏa mãn \(\overline z - 3 + i = 0.\) Modun của \(z\) bằng:
- A \(4.\)
- B \(10.\)
- C \(\sqrt 3 .\)
- D \(\sqrt {10} .\)
Đáp án: D
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\)
Khi đó modun của số phức \(z\) là:\(\left| z \right| = \sqrt {{a^2} + {b^2}} .\)
Lời giải chi tiết:
Ta có: \(\overline z - 3 + i = 0 \Leftrightarrow \overline z = 3 - i \Rightarrow z = 3 + i.\)
\( \Rightarrow \left| z \right| = \sqrt {{3^2} + 1} = \sqrt {10} .\)
Chọn D.
Câu hỏi 18 :
Cho \({z_1} = 2 - i,\,{z_2} = - 3 + i\). Phần ảo của số phức \(z = 2{z_1} + 3i{z_2}\) bằng
- A \(17\).
- B \( - 11\).
- C \( - 19\).
- D \(22\)
Đáp án: B
Phương pháp giải:
- Thực hiện phép nhân và cộng số phức.
- Số phức \(z = a + bi\) có phần ảo bằng b.
Lời giải chi tiết:
\(\begin{array}{l}z = 2{z_1} + 3i{z_2} = 2\left( {2 - i} \right) + 3i\left( { - 3 + i} \right)\\\,\,\,\, = 4 - 2i - 9i - 3 = 1 - 11i\end{array}\)
Vậy phần ảo của số phức \(z\) bằng -11.
Chọn B.
Câu hỏi 19 :
Cho số phức \(z = 1 - 2i\). Môđun của số phức \(iz + \overline z \) bằng:
- A \(\sqrt 6 \)
- B \(3\sqrt 2 \)
- C \(\sqrt {10} \)
- D \(6\)
Đáp án: B
Phương pháp giải:
- Tính số phức z.
- Áp dụng công thức tính môđun số phức: \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}iz + \overline z = i\left( {1 - 2i} \right) + \left( {1 + 2i} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = i + 2 + 1 + 2i = 3 + 3i\\ \Rightarrow \left| {iz + \overline z } \right| = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 .\end{array}\)
Chọn B.
Câu hỏi 20 :
Cho số phức \(z = 2 - 3i\). Mô-đun của số phức \(w = 2z + \left( {1 + i} \right)\bar z\) bằng:
- A \(4\)
- B \(2\)
- C \(\sqrt {10} \)
- D \(2\sqrt 2 \)
Đáp án: C
Phương pháp giải:
- Số phức \(z = a + bi\) có số phức liên hợp \(\bar z = a - bi\).
- Thực hiện phép nhân tìm số phức \(w\).
- Sử dụng công thức tính môđun số phức: \(z = a + bi\)\( \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}w = 2z + \left( {1 + i} \right)\bar z\\w = 2\left( {2 - 3i} \right) + \left( {1 + i} \right)\left( {2 + 3i} \right)\\w = 4 - 6i + 2 + 3i + 2i - 3\\w = 3 - i\\ \Rightarrow \left| w \right| = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} .\end{array}\)
Chọn C.
Câu hỏi 21 :
Cho hai số phức \({z_1} = 2 + 3i\) và \({z_2} = 1 - i.\) Tính modun của số phức \({z_1} + {z_2}.\)
- A \(5\)
- B \(\sqrt 5 \)
- C \(13\)
- D \(\sqrt {13} \)
Đáp án: D
Phương pháp giải:
Cho \({z_1} = {a_1} + {b_1}i;\,\,{z_2} = {a_2} + {b_2}i\,\,\,\left( {{a_1},\,\,{a_2},\,\,{b_1},\,\,{b_2} \in \mathbb{R}} \right).\) Ta có: \({z_1} + {z_2} = {a_1} + {a_2} + \left( {{b_1} + {b_2}} \right)i.\)
\( \Rightarrow \left| {{z_1} + {z_2}} \right| = \sqrt {{{\left( {{a_1} + {a_2}} \right)}^2} + {{\left( {{b_1} + {b_2}} \right)}^2}} .\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{z_1} = 2 + 3i\\{z_2} = 1 - i\end{array} \right. \Rightarrow {z_1} + {z_2} = 3 + 2i\) \( \Rightarrow \left| {{z_1} + {z_2}} \right| = \sqrt {{3^2} + {2^2}} = \sqrt {13} .\)
Chọn D.
Câu hỏi 22 :
Biết \({z_1},\,\,{z_2}\) là hai nghiệm của phương trình \(2{z^2} - 3z + 4 = 0\). Khi đó \(z_1^2 + z_2^2\) bằng
- A \(\dfrac{{25}}{4}\)
- B \( - \dfrac{5}{2}\)
- C \( - \dfrac{7}{4}\)
- D \(\dfrac{7}{2}\)
Đáp án: C
Phương pháp giải:
Biến đổi biểu thức làm xuất hiện \({z_1} + {z_2}\) và \({z_1}{z_2}\).
Sử dụng định lí Vi-et \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \dfrac{b}{a}\\{z_1}{z_2} = \dfrac{c}{a}\end{array} \right.\)
Thay vào biểu thức cần tính giá trị.
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{z_1} + {z_2} = \dfrac{3}{2}\\{z_2}.{z_2} = 2\end{array} \right.\)
Khi đó
\(\begin{array}{l}z_1^2 + z_2^2 = {\left( {{z_1} + {z_2}} \right)^2} - 2{z_1}{z_2}\\ = {\left( {\dfrac{3}{2}} \right)^2} - 2.2 = - \dfrac{7}{4}\end{array}\)
Chọn C.
Câu hỏi 23 :
Cho số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) thỏa mãn \(z - 2\bar z = - 1 + 6i\). Giá trị \(a + b\) bằng:
- A \( - 1\)
- B \( - 3\)
- C \(2\)
- D \(3\)
Đáp án: D
Phương pháp giải:
- Thực hiện phép nhân và trừ số phức.
- Hai số phức \({z_1} = {a_1} + {b_1}i\), \({z_2} = {a_2} + {b_2}i\) bằng nhau khi và chỉ khi \(\left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} = {b_2}\end{array} \right.\).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\,\,\,\,\left( {a + bi} \right) - 2\left( {a - bi} \right) = - 1 + 6i\\ \Leftrightarrow - a + 3bi = - 1 + 6i\\ \Leftrightarrow \left\{ \begin{array}{l} - a = - 1\\3b = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\end{array} \right.\end{array}\)
Vậy \(a + b = 1 + 2 = 3\).
Chọn D.
Câu hỏi 24 :
Trên mặt phẳng tọa độ, cho hai số phức \({z_1} = 2 + i\) và \({z_2} = 1 - i.\) Điểm biểu diễn số phức \({z_1} - {z_2}\) là điểm nào dưới đây?
- A \(Q\left( {1; - 2} \right)\)
- B \(M\left( {1;\,\,0} \right)\)
- C \(P\left( {2;\,\,1} \right)\)
- D \(N\left( {1;\,\,2} \right)\)
Đáp án: D
Phương pháp giải:
Cho \({z_1} = {a_1} + {b_1}i;\,\,{z_2} = {a_2} + {b_2}i\,\,\,\left( {{a_1},\,\,{a_2},\,\,{b_1},\,\,{b_2} \in \mathbb{R}} \right).\) Ta có: \({z_1} \pm {z_2} = {a_1} \pm {a_2} + \left( {{b_1} \pm {b_2}} \right)i.\)
Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{z_1} = 2 + i\\{z_2} = 1 - i\end{array} \right.\) \( \Rightarrow {z_1} - {z_2} = \left( {2 - 1} \right) + \left( {1 + 1} \right)i = 1 + 2i\)
\( \Rightarrow N\left( {1;\,2} \right)\) là điểm biểu diễn số phức \({z_1} - {z_2}.\)
Chọn D.
Câu hỏi 25 :
Trong hình bên .\(M,\,\,N\). lần lượt là điểm biểu diễn số phức \(z\) và \({\rm{w}}{\rm{.}}\) Số phức \(z + {\rm{w}}\) bằng?
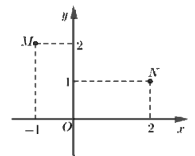
- A \(1 - 3i\)
- B \(3 + i\)
- C \(1 + 3i\)
- D \(3 - i\)
Đáp án: C
Phương pháp giải:
Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\)
Cho hai số phức: \({z_1} = {a_1} + {b_1}i,\,\,\,{z_2} = {a_2} + {b_2}i\,\,\,\,\left( {{a_1},\,\,{b_1},\,\,{a_2},\,\,{b_2} \in \mathbb{R}} \right).\) Khi đó: \({z_1} + {z_2} = \left( {{a_1} + {a_2}} \right) + \left( {{b_1} + {b_2}} \right)i.\)
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy: \(M\left( { - 1;\,\,2} \right) \Rightarrow z = - 1 + 2i\) và \(N\left( {2;\,\,1} \right) \Rightarrow {\rm{w}} = 2 + i.\)
Khi đó ta có: \(z + {\rm{w}} = - 1 + 2i + 2 + i = 1 + 3i.\)
Chọn C.
Câu hỏi 26 :
Cho số phức \(z\) thỏa mãn \(z\left( {1 + i} \right) = 3 - 5i\). Tính môđun của \(z\).
- A \(\left| z \right|=\sqrt{17}\).
- B \(\left| z \right|=16\).
- C \(\left| z \right|=17\).
- D \(\left| z \right|=4\).
Đáp án: A
Phương pháp giải:
Chia số phức và tính môđun của số phức tìm được (bấm máy)
Lời giải chi tiết:
Ta có \(z\left( 1+i \right)=3-5i\Leftrightarrow z=\frac{3-5i}{1+i}=\frac{\left( 3-5i \right)\left( 1-i \right)}{1-{{i}^{2}}}=-1-4i\Rightarrow \left| z \right|=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=\sqrt{17}.\)
Chọn A
Câu hỏi 27 :
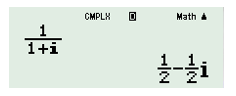
Phần ảo của số phức \(\frac{1}{{1 + i}}\) là :
- A \(\frac{1}{2}\)
- B \( - \frac{1}{2}\)
- C \( - \frac{1}{2}i\)
- D \( - 1\)
Đáp án: B
Phương pháp giải:
Sử dụng MTCT, đưa z về dạng \(z = a + bi\) và kết luận số phức z có phần ảo bằng b.
Lời giải chi tiết:
Chọn B.
Câu hỏi 28 :
Tìm phần thực , phần ảo của số phức sau : \(\) \(z=\frac{3-i}{1+i}+\frac{2+i}{i}\)
- A Phần thực là 2; phần ảo là -4
- B Phần thực là 2; phần ảo là 4i
- C Phần thực là 2; phần ảo là 4
- D Phần thực là 2;phần ảo là -4i
Đáp án: A
Phương pháp giải:
cho z = a + bi , phần thực của z là a ; phần ảo của z là b
Lời giải chi tiết:
\(z=\frac{3-i}{1+i}+\frac{2+i}{i}=2-4i\)
Suy ra phần thực là 2 ; phần ảo là -4
Chọn đáp án A
Câu hỏi 29 :
Tìm phần ảo của số phức \(z = \dfrac{3}{i}\).
- A \( - 1\).
- B \(1\)
- C \( - 3\).
- D \(3\).
Đáp án: C
Phương pháp giải:
Số phức \(z = a + bi,\left( {a,b \in \mathbb{R}} \right)\) có phần thực là \(a\), phần ảo là \(b\).
Lời giải chi tiết:
Ta có: \(z = \dfrac{3}{i} = \dfrac{{3i}}{{{i^2}}} = - 3i\): có phần ảo là \( - 3\).
Chọn: C
Câu hỏi 30 :
Số phức liên hợp của số phức \(z = \dfrac{2}{{i + 1}}\) là:
- A \(\dfrac{{ - 2}}{{1 - i}}\).
- B \(1 - i\).
- C \(\dfrac{{ - 2}}{{1 + i}}\).
- D \(1 + i\).
Đáp án: D
Phương pháp giải:
Số phức liên hợp của số phức \(z = a + bi,\left( {a,b \in \mathbb{R}} \right)\) là \(\overline z = a - bi\).
Lời giải chi tiết:
Ta có: \(z = \dfrac{2}{{i + 1}} = \dfrac{{2\left( {i - 1} \right)}}{{\left( {i + 1} \right)\left( {i - 1} \right)}} = \dfrac{{2\left( {i - 1} \right)}}{2} = 1 - i\)
Số phức liên hợp của z là \(\overline z = 1 + i\).
Chọn: D
Câu hỏi 31 :
Tìm số phức \(z\) biết: \(\left( {1 - i} \right)z - 1 + 5i = 0\).
- A \(z = - 3 - 2i\)
- B \(z = 3 - 2i\)
- C \(z = 3 + 2i\)
- D \(z = - 3 + 2i\)
Đáp án: B
Phương pháp giải:
Thực hiện phép chia số phức tìm \(z\).
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,\,\,\left( {1 - i} \right)z - 1 + 5i = 0\\ \Leftrightarrow \left( {1 - i} \right)z = 1 - 5i\\ \Leftrightarrow z = \dfrac{{1 - 5i}}{{1 - i}} = 3 - 2i.\end{array}\)
Chọn B.
Câu hỏi 32 :
Số phức \(z = \dfrac{{5 + 15i}}{{3 + 4i}}\) có phần thực là
- A \(3.\)
- B \(1.\)
- C \(-3.\)
- D \(-1.\)
Đáp án: A
Phương pháp giải:
Tính số phức z bằng MTCT sau đó suy ra phần thực.
Lời giải chi tiết:
\(z = \dfrac{{5 + 15i}}{{3 + 4i}} = 3 + i\)

Vậy phần thực của z bằng 3.
Chọn A.
Câu hỏi 33 :
Số phức liên hợp \(\overline z \) của số phức \(z = \dfrac{{4 + 6i}}{{1 - i}}\) là:
- A \(\overline z = - 2 - 10i\)
- B \(\overline z = - 1 + 5i\)
- C \(\overline z = - 2 + 10i\)
- D \(\overline z = - 1 - 5i\)
Đáp án: D
Phương pháp giải:
- Tìm số phức z bằng MTCT.
- Số phức liên hợp của số phức \(z = a + bi\) là \(\overline z = a - bi\).
Lời giải chi tiết:
Ta có \(z = \dfrac{{4 + 6i}}{{1 - i}} = - 1 + 5i \Rightarrow \overline z = - 1 - 5i.\)
Chọn D.
Câu hỏi 34 :
Cho số phức z thỏa mãn \(z\left( {1 + i} \right) = 7 + i\). Môđun của số phức z bằng
- A \(2\sqrt {10} \)
- B 25.
- C 40
- D 5
Đáp án: D
Phương pháp giải:
- Tìm số phức z bằng MTCT hoặc thực hiện phép chia.
- Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết:
Ta có \(z\left( {1 + i} \right) = 7 + i \Rightarrow z = \dfrac{{7 + i}}{{1 + i}} = 4 - 3i\)
Khi đó \(\left| z \right| = \sqrt {{4^2} + {{\left( { - 3} \right)}^2}} = 5.\)
Chọn D.
Câu hỏi 35 :
Cho số phức z thỏa mãn \(\left( {1 + 3i} \right)z - 5 = 7i\). Khi đó số phức liên hợp của z là
- A \(\overline z = \dfrac{{13}}{5} - \dfrac{4}{5}i\)
- B \(\overline z = - \dfrac{{13}}{5} + \dfrac{4}{5}i\)
- C \(\overline z = - \dfrac{{13}}{5} - \dfrac{4}{5}i\)
- D \(\overline z = \dfrac{{13}}{5} + \dfrac{4}{5}i\)
Đáp án: D
Phương pháp giải:
- Thực hiện phép chia số phức.
- Số phức liên hợp của số phức \(z = a + bi\) là \(\overline z = a - bi\).
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,\,\,\,\left( {1 + 3i} \right)z - 5 = 7i\\ \Leftrightarrow z = \dfrac{{7i + 5}}{{1 + 3i}} = \dfrac{{13}}{5} - \dfrac{4}{5}i\\ \Rightarrow \overline z = \dfrac{{13}}{5} + \dfrac{4}{5}i\end{array}\)
Chọn D.
Câu hỏi 36 :
Gọi \(z,{\rm{w}}\) là các số phức có điểm biểu diễn lần lượt là \(M,\,\,N\) trên mặt phẳng Oxy như hình minh họa bên. Phần ảo của số phức \(\dfrac{z}{{\rm{w}}}\) là
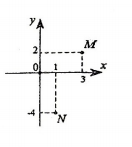
- A \(\dfrac{{14}}{{17}}\)
- B \(3\)
- C \( - \dfrac{5}{{17}}\)
- D \( - \dfrac{1}{2}\)
Đáp án: A
Phương pháp giải:
- Từ đồ thị suy ra tọa độ của M, N.
- Tìm hai số phức z, w: Điểm \(M\left( {a;b} \right)\) biểu diễn cho số phức \(z = a + bi\).
- Tính \(\dfrac{z}{{\rm{w}}}\), sử dụng MTCT.
Lời giải chi tiết:
Dựa vào đồ thị ta có \(M\left( {3;2} \right),\)\(N\left( {1; - 4} \right).\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}z = 3 + 2i\\{\rm{w}} = 1 - 4i\end{array} \right.\\ \Rightarrow \dfrac{z}{{\rm{w}}} = \dfrac{{3 + 2i}}{{1 - 4i}} = - \dfrac{5}{{17}} + \dfrac{{14}}{{17}}i\end{array}\)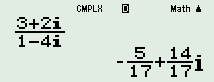
Khi đó phần ảo của số phức \(\dfrac{z}{{\rm{w}}}\) là \(\dfrac{{14}}{{17}}\)
Chọn A.
Câu hỏi 37 :
Nghiệm của phương trình \(\left( {3 + i} \right)z + \left( {4 - 5i} \right) = 6 - 3i\) là
- A \(z = \dfrac{2}{5} + \dfrac{4}{5}i\)
- B \(z = \dfrac{1}{2} + \dfrac{1}{2}i\)
- C \(z = \dfrac{4}{5} + \dfrac{2}{5}i\)
- D \(z = 1 + \dfrac{1}{2}i\)
Đáp án: C
Phương pháp giải:
- Biến đổi phương trình số phức, giải phương trình dạng \(az = b \Leftrightarrow z = \dfrac{b}{a}\).
- Sử dụng MTCT để thực hiện phép chia số phức.
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,\,\,\left( {3 + i} \right)z + \left( {4 - 5i} \right) = 6 - 3i\\ \Leftrightarrow \left( {3 + i} \right)z = 6 - 3i - \left( {4 - 5i} \right)\\ \Leftrightarrow \left( {3 + i} \right)z = 2 + 2i\\ \Leftrightarrow z = \dfrac{{2 + 2i}}{{3 + i}} = \dfrac{4}{5} + \dfrac{2}{5}i\end{array}\)
Chọn C.
Câu hỏi 38 :
Cho \(z = 1 + \sqrt 3 i\). Tìm số phức nghịch đảo của số phức\(z\).
- A \(\dfrac{1}{z} = \dfrac{1}{4} + \dfrac{{\sqrt 3 }}{4}i\)
- B \(\dfrac{1}{z} = \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i\)
- C \(\dfrac{1}{z} = \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\)
- D \(\dfrac{1}{z} = \dfrac{1}{4} - \dfrac{{\sqrt 3 }}{4}i\)
Đáp án: D
Phương pháp giải:
Số phức nghịch đảo của số phức z là \(\dfrac{1}{z}\).
Lời giải chi tiết:
\(\dfrac{1}{z} = \dfrac{1}{{1 + \sqrt 3 i}} = \dfrac{1}{4} - \dfrac{{\sqrt 3 }}{4}i.\)
Chọn D.
Câu hỏi 39 :
Cho số phức \(z = a + bi\) với \(a;b \in \mathbb{R}\) thỏa mãn \(\left( {1 + i} \right)z + \left( {2 - i} \right)\overline z = 13 + 2i.\) Tính tổng \(a + b\)
- A \(a + b = 1.\)
- B \(a + b = - 2.\)
- C \(a + b = 2.\)
- D \(a + b = 0.\)
Đáp án: A
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\)
Lời giải chi tiết:
Ta có: \(z = a + bi \Rightarrow \overline z = a - bi.\)
\(\begin{array}{l} \Rightarrow \left( {1 + i} \right)z + \left( {2 - i} \right)\overline z = 13 + 2i\\ \Leftrightarrow \left( {1 + i} \right)\left( {a + bi} \right) + \left( {2 - i} \right)\left( {a - bi} \right) = 13 + 2i\\ \Leftrightarrow a + ai + bi + b{i^2} + 2a - 2bi - ai + b{i^2} = 13 + 2i\\ \Leftrightarrow 3a - 2b - bi = 13 + 2i\\ \Leftrightarrow \left\{ \begin{array}{l}3a - 2b = 13\\ - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 2\end{array} \right.\\ \Rightarrow a + b = 3 - 2 = 1.\end{array}\)
Chọn A.
Câu hỏi 40 :
Trên \(\mathbb{C}\) phương trình \(\dfrac{2}{{z - 1}} = 1 + i\) có nghiệm là:
- A \(z = 2 - i.\)
- B \(z = 1 - 2i.\)
- C \(z = 1 + 2i.\)
- D \(z = 2 + i.\)
Đáp án: A
Phương pháp giải:
Thực hiện phép chia số phức.
Lời giải chi tiết:
\(\dfrac{2}{{z - 1}} = 1 + i \Leftrightarrow z - 1 = \dfrac{2}{{1 + i}} \Leftrightarrow z - 1 = 1 - i \Leftrightarrow z = 2 - i\).
Chọn A.
Câu hỏi 41 :
Cho hai số phức \({z_1} = 5 - i\), \({z_2} = 1 + i\). Phần thực của số phức \(\dfrac{{{z_1}}}{{{z_2}}}\) bằng:
- A \(6\)
- B \(2\)
- C \(-3\)
- D \(4\)
Đáp án: B
Phương pháp giải:
Sử dụng: \(\dfrac{{{z_1}}}{{{z_2}}} = \dfrac{{{a_1} + {b_1}i}}{{{a_2} + {b_2}i}}\)\( = \dfrac{{\left( {{a_1} + {b_1}i} \right)\left( {{a_2} - {b_2}i} \right)}}{{a_2^2 + b_2^2}}\)
Lời giải chi tiết:
Ta có: \(\dfrac{{{z_1}}}{{{z_2}}}\)\( = \dfrac{{5 - i}}{{1 + i}} = \dfrac{{\left( {5 - i} \right)\left( {1 - i} \right)}}{{{1^2} - {i^2}}}\)\( = \dfrac{{5 - 6i + {i^2}}}{2}\)\( = \dfrac{{4 - 6i}}{2} = 2 - 3i\)
Số phức \(2 - 3i\) có phần thực bằng \(2.\)
Chọn B.
Câu hỏi 42 :
Số phức nghịch đảo của \(z = 3 + 4i\) là:
- A \(3 - 4i\)
- B \(\dfrac{3}{{25}} - \dfrac{4}{{25}}i\)
- C \(\dfrac{3}{{25}} + \dfrac{4}{{25}}i\)
- D \(\dfrac{3}{5} - \dfrac{4}{5}i\)
Đáp án: B
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right).\) Khi đó số phức nghịch đảo của số phức \(z\) là: \(\dfrac{1}{z} = \dfrac{1}{{a + bi}}.\)
Lời giải chi tiết:
Số phức nghịch đảo của số phức \(z = 3 + 4i\) là: \(\dfrac{1}{{3 + 4i}} = \dfrac{{3 - 4i}}{{{3^2} - {{\left( {4i} \right)}^2}}}\) \( = \dfrac{{3 - 4i}}{{9 + 16}} = \dfrac{3}{{25}} - \dfrac{4}{{25}}i.\)
Chọn B.
Câu hỏi 43 :
Phần thực của số phức \(z = \left( {1 + 2i} \right) + \dfrac{i}{{1 + i}}\) bằng:
- A \(\dfrac{3}{2}\)
- B \(1 - \dfrac{{\sqrt 2 }}{2}\)
- C \(1 + \dfrac{{\sqrt 2 }}{2}\)
- D \(\dfrac{1}{2}\)
Đáp án: A
Phương pháp giải:
- Sử dụng MTCT tìm số phức \(z\).
- Số phức \(z = a + bi\) có phần thực bằng \(a\).
Lời giải chi tiết:
Sử dụng MTCT ta có: 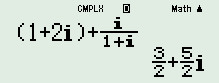 \( \Rightarrow z = \dfrac{3}{2} + \dfrac{5}{2}i\).
\( \Rightarrow z = \dfrac{3}{2} + \dfrac{5}{2}i\).
Vậy số phức \(z\) có phần thực bằng \(\dfrac{3}{2}\).
Chọn A.
Câu hỏi 44 :
Biết số phức \(z\) thỏa mãn \({z^{ - 1}} = 1 + 2i,\) phần ảo của \(z\) bằng:
- A \(\dfrac{1}{5}\)
- B \( - \dfrac{1}{5}\)
- C \( - \dfrac{2}{5}\)
- D \(\dfrac{2}{5}\)
Đáp án: C
Phương pháp giải:
Ta có:\({z^{ - 1}} = \dfrac{1}{z}.\)
Số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có phần thực là \(a\) và phần ảo là \(b.\)
Lời giải chi tiết:
Ta có: \({z^{ - 1}} = 1 + 2i\) \( \Rightarrow \dfrac{1}{z} = 1 + 2i\) \( \Leftrightarrow z = \dfrac{1}{{1 + 2i}} = \dfrac{{1 - 2i}}{{1 - {{\left( {2i} \right)}^2}}}\)\( = \dfrac{{1 - 2i}}{{1 + 4}} = \dfrac{1}{5} - \dfrac{2}{5}i\)
\( \Rightarrow \) Số phức \(z\) có phần ảo là \( - \dfrac{2}{5}.\)
Chọn C.
Câu hỏi 45 :
Cho số phức \(z\) thỏa mãn \(iz = 1 + 3i.\) Modun của \(z\) bằng:
- A \(\sqrt {10} \)
- B \(4\)
- C \(2\sqrt 2 \)
- D \(2\)
Đáp án: A
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right),\) ta có modun của số phức \(z\) là:\(\left| z \right| = \sqrt {{a^2} + {b^2}} .\)
Lời giải chi tiết:
Ta có: \(iz = 1 + 3i\) \( \Rightarrow z = \dfrac{{1 + 3i}}{i} = \dfrac{{i + 3{i^2}}}{{{i^2}}} = 3 - i\) \( \Rightarrow \left| z \right| = \sqrt {{3^2} + 1} = \sqrt {10} .\)
Chọn A.
Câu hỏi 46 :
Số phức liên hợp của số phức \(z = \dfrac{1}{{1 + i}}\) là:
- A \(\dfrac{1}{2} + \dfrac{1}{2}i\)
- B \(1 + i\)
- C \(1 - i\)
- D \(\dfrac{1}{2} - \dfrac{1}{2}i\)
Đáp án: A
Phương pháp giải:
Tìm số phức \(z = a + bi \Rightarrow \overline z = a - bi\) là số phức liên hợp của z.
Lời giải chi tiết:
Ta có \(z = \dfrac{1}{{1 + i}} = \dfrac{1}{2} - \dfrac{1}{2}i \Rightarrow \overline z = \dfrac{1}{2} + \dfrac{1}{2}i\).
Chọn A.
Câu hỏi 47 :
Cho số phức \(z = a + bi\) (với \(a,b \in \mathbb{R}\)) thỏa mãn \(z\left( {\overline {1 + 2i} } \right) + i = 3\). Tính \(T = a + b\).
- A \(T = - \dfrac{6}{5}\).
- B \(T = 0\).
- C \(T = 2\).
- D \(T = 1\).
Đáp án: C
Phương pháp giải:
- Thực hiện phép chia số phức để tìm \(z\).
- Đồng nhất hệ số tìm \(a,\,\,b\) và tính tổng \(T = a + b\).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,z\left( {\overline {1 + 2i} } \right) + i = 3 \Leftrightarrow z.\left( {1 - 2i} \right) = 3 - i\\ \Leftrightarrow z = \dfrac{{3 - i}}{{1 - 2i}} = \dfrac{{\left( {3 - i} \right)\left( {1 + 2i} \right)}}{5} = 1 + i\end{array}\)
\( \Rightarrow a = b = 1 \Rightarrow T = a + b = 2\).
Chọn C.
Câu hỏi 48 :
Cho hai số phức \({z_1} = 2 - 3i,\,\,{z_2} = - 3 + 6i.\) Khi đó số phức \({z_1} + {z_2}\) bằng:
- A \(1 - 9i\)
- B \( - 1 - 9i\)
- C \(1 + 3i\)
- D \( - 1 + 3i\)
Đáp án: D
Phương pháp giải:
Cho \({z_1} = {a_1} + {b_1}i;\,\,{z_2} = {a_2} + {b_2}i\,\,\,\left( {{a_1},\,\,{a_2},\,\,{b_1},\,\,{b_2} \in \mathbb{R}} \right).\) Khi đó ta có: \({z_1} + {z_2} = {a_1} + {a_2} + \left( {{b_1} + {b_2}} \right)i.\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{z_1} = 2 - 3i\\\,{z_2} = - 3 + 6i\end{array} \right.\) \( \Rightarrow {z_1} + {z_2}\) \( = \left( {2 - 3} \right) + \left( { - 3 + 6} \right)i\) \( = - 1 + 3i.\)
Chọn D.
Câu hỏi 49 :
Cho hai số phức \({z_1} = 2 + 3i\), \({z_2} = - 4 + i\). Phần ảo của số phức \({z_1} - {z_2}\) bằng
- A \(4i\)
- B \(2i\)
- C \(2\)
- D \(4\)
Đáp án: C
Phương pháp giải:
Cho \({z_1} = {a_1} + {b_1}i;{z_2} = {a_2} + {b_2}i\) với \({a_1},{b_1},{a_2},{b_2} \in \mathbb{R}\)
Ta có: \({z_1} - {z_2} = \left( {{a_1} - {a_2}} \right) + \left( {{b_1} - {b_2}} \right)i\)
Lời giải chi tiết:
Ta có: \({z_1} - {z_2}\)\( = 2 + 3i - \left( { - 4 + i} \right)\)\( = 2 + 3i + 4 - i\)\( = 6 + 2i\)
Phần ảo của số phức \(6 + 2i\) là \(2.\)
Chọn C.
Câu hỏi 50 :
Phần thực của số phức \(\left( {2 - i} \right)\left( {1 + 2i} \right)\) là:
- A \(4.\)
- B \(5.\)
- C \(3.\)
- D \(0.\)
Đáp án: A
Phương pháp giải:
Tính số phức z bằng MTCT và suy ra phần thực của nó.
Lời giải chi tiết:
Ta có \(z = \left( {2 - i} \right)\left( {1 + 2i} \right) = 4 + 3i.\)
Vậy phần thực của số phức z là 4.
Chọn A.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục