40 bài tập trắc nghiệm mặt trụ mức độ vận dụng, vận dụng cao
Làm đề thiCâu hỏi 1 :
Cho hình trụ bán kính đường tròn đáy bằng 1. Hai điểm \(A\) và \(B\) lần lượt thuộc hai đường tròn đáy sao cho \(AB = \sqrt 6 \), khoảng cách giữa hai đường thẳng \(AB\) và trục của hình trụ bằng \(\dfrac{1}{2}\). Thể tích khối trụ được giới hạn bởi hình trụ đó bằng:
- A \(6\pi \)
- B \(\pi \sqrt 6 \)
- C \(\pi \sqrt 3 \)
- D \(3\pi \)
Đáp án: C
Phương pháp giải:
- Gọi \(A'\) là hình chiếu của \(A\) lên đường tròn đáy chứa điểm \(B\). Sử dụng định lí: Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa đường thẳng này và mặt phẳng song song chứa đường thẳng kia, chứng minh \(d\left( {OO';AB} \right) = d\left( {O';\left( {AA'B} \right)} \right)\).
- Gọi \(H\) là trung điểm của \(A'B\), chứng minh \(O'H \bot \left( {AA'B} \right)\).
- Sử dụng định lí Pytago trong tam giác vuông tính chiều cao của hình trụ.
- Thể tích khối trụ có chiều cao , bán kính đáy \(r\) là .
Lời giải chi tiết:
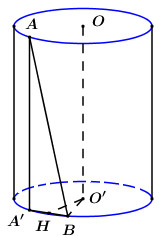
Gọi \(O,\,\,O'\) lần lượt là tâm đường tròn đáy chứa \(A,\,\,B\).
Gọi \(A'\) là hình chiếu của \(A\) lên đường tròn đáy chứa điểm \(B\).
Ta có \(AA'\parallel OO' \Rightarrow OO'\parallel \left( {AA'B} \right) \supset AB\) \( \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {AA'B} \right)} \right) = d\left( {O';\left( {AA'B} \right)} \right)\).
Gọi \(H\) là trung điểm của \(A'B\), ta có \(O'H \bot A'B\) (quan hệ vuông góc giữa đường kính và dây cung).
Khi đó ta có: \(\left\{ \begin{array}{l}O'H \bot A'B\\O'H \bot AA'\end{array} \right. \Rightarrow O'H \bot \left( {AA'B} \right)\) \( \Rightarrow d\left( {OO';AB} \right) = OH = \dfrac{1}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(O'HB\) có \(HB = \sqrt {O'{B^2} - O'{H^2}} = \sqrt {{1^2} - {{\left( {\dfrac{1}{2}} \right)}^2}} = \dfrac{{\sqrt 3 }}{2}\).
\( \Rightarrow A'B = 2HB = \sqrt 3 \).
Áp dụng định lí Pytago trong tam giác vuông có: \(AA' = \sqrt {A{B^2} - A'{B^2}} = \sqrt {6 - 3} = \sqrt 3 \).
Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi {.1^2}.\sqrt 3 = \pi \sqrt 3 \).
Chọn C.
Câu hỏi 2 :
Một hình trụ có diện tích xung quanh là \(16\pi \), thiết diện qua trục là hình vuông. Một mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo thiết diện là \(ABB'A'\), biết một cạnh thiết diện là một dây của đường tròn đáy hình trụ và căng một cung \({120^0}\). Chu vi tứ giác \(ABB'A'\) bằng:
- A \(4 + 2\sqrt 3 \)
- B \(8\sqrt 3 \)
- C \(16 + 8\sqrt 3 \)
- D \(8 + 4\sqrt 3 \)
Đáp án: D
Phương pháp giải:
- Gọi \(r,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ, vì thiết diện qua trục là hình vuông nên \(h = 2r\). Dựa vào diện tích xung quanh của hình trụ tính \(r,\,\,h\).
- Dựa vào định lí Cosin trong tam giác \(OAB\) tính \(AB\) theo \(r\), từ đó tính được \(AB\).
- Sử dụng công thức tính chu vi hình chữ nhật \({C_{ABB'A'}} = 2\left( {AB + AA'} \right)\).
Lời giải chi tiết:
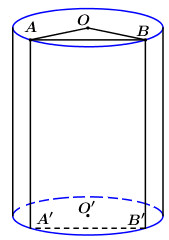
Gọi \(r,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ, ta có \({S_{xq}} = 2\pi rh \Leftrightarrow 16\pi = 2\pi rh \Leftrightarrow rh = 8\).
Lại có thiết diện qua trục là hình vuông nên \(h = 2r\), do đó \(r.2r = 8 \Leftrightarrow {r^2} = 4\) \( \Rightarrow r = 2,\,\,h = 4 = AA'\).
Theo bài ra ta có: \(\angle AOB = {120^0}\).
Áp dụng định lí Cosin trong tam giác \(OAB\) ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \angle AOB\\A{B^2} = {r^2} + {r^2} - 2.r.r.\cos {120^0}\\A{B^2} = 3{r^2}\\ \Rightarrow AB = r\sqrt 3 = 2.\sqrt 3 \end{array}\)
Vậy \({C_{ABB'A'}} = 2\left( {AB + AA'} \right) = 2\left( {2\sqrt 3 + 4} \right) = 8 + 4\sqrt 3 \).
Chọn D.
Câu hỏi 3 :
Cho tứ diện đều ABCD có cạnh bằng 4. Hình trụ \(\left( T \right)\) có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD. Diện tích xung quanh của \(\left( T \right)\) bằng:
- A \(\frac{{16\sqrt 2 \pi }}{3}.\)
- B \(8\sqrt 2 \pi .\)
- C \(\frac{{16\sqrt 3 \pi }}{3}.\)
- D \(8\sqrt 3 \pi .\)
Đáp án: A
Phương pháp giải:
- Tìm bán kính đáy của hình trụ là bán kính đường tròn nội tiếp tam giác BCD.
- Tìm chiều cao hình trụ chính là chiều cao hình chóp ABCD.
- Áp dụng công thức tính diện tích xung quanh hình trụ: \(S = 2\pi Rh\)
Lời giải chi tiết:
Tam giác BCD là tam giác đều cạnh 4\( \Rightarrow \left\{ \begin{array}{l}{S_{BCD}} = 4\sqrt 3 \\p = 12\end{array} \right.\)
Áp dụng cồn thức tính bán kính đường tròn nội tiếp ta có:\(R = \frac{{2S}}{p} = \frac{{2\sqrt 3 }}{3}\)
Gọi O là tâm của tam giác đều BCD
\( \Rightarrow AO \bot \left( {BCD} \right) \Rightarrow \Delta ABO\) vuông tại O có \(BO = \frac{{4\sqrt 3 }}{3};AB = 4 \Rightarrow AO = h = \frac{{4\sqrt 6 }}{3}\)
Khi đó diện tích xung quanh hình trụ có \(h = \frac{{4\sqrt 6 }}{3};R = \frac{{2\sqrt 3 }}{3}\) là \(S = 2\pi Rh = \frac{{16\sqrt 2 \pi }}{3}\)
Chọn A.
Câu hỏi 4 :
Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \dfrac{2}{\pi }\,\,cm\) (như hình vẽ).
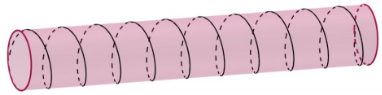
Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó.
- A \(80\,\,c{m^2}\)
- B \(100\,\,c{m^2}\)
- C \(60\,\,c{m^2}\)
- D \(120\,\,c{m^2}\)
Đáp án: D
Phương pháp giải:
- Gọi độ dài đường cao của ống trụ là \(10x\,\,\left( {cm} \right)\,\,\left( {x > 0} \right)\).
- Chia ống trụ thành 10 phần bằng nhau, trải phẳng mỗi ống trụ nhỏ ta được 1 hình chữ nhật, xác định hai kích thước của hình chữ nhật đó.
- Độ dài đường chéo của hình chữ nhật là độ dài 1 vòng dây, lập phương trình tìm \(x\).
- Diện tích xung quanh hình trụ có chiều cao \(h\), bán kính đáy \(R\) là \({S_{xq}} = 2\pi Rh\).
Lời giải chi tiết:
Gọi độ dài đường cao của ống trụ là \(10x\,\,\left( {cm} \right)\,\,\left( {x > 0} \right)\).
Chia ống trụ thành 10 phần bằng nhau, mỗi phần có độ dài đường sinh là \(x\,\,\left( {cm} \right)\).
Trải phẳng mỗi ống trụ nhỏ ta được 1 hình chữ nhật có hai kích thước là \(x\) và \(2\pi .R = 2\pi .\dfrac{2}{\pi } = 4\,\,\left( {cm} \right)\).
Khi đó độ dài đường chéo của hình chữ nhật là \(\sqrt {{x^2} + {4^2}} = \sqrt {{x^2} + 16} \), và độ dài đường chéo chính bằng độ dài của 1 vòng.
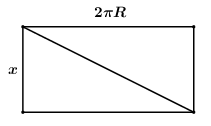
Do đó ta có phương trình: \(10\sqrt {{x^2} + 16} = 50 \Leftrightarrow \sqrt {{x^2} + 16} = 5\) \( \Rightarrow {x^2} + 16 = 25 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = 3\,\,\left( {cm} \right)\,\,\left( {tm} \right)\).
\( \Rightarrow \) Độ dài đường cao của ống trụ là \(h = 10x = 30\,\,\left( {cm} \right)\).
Vậy diện tích xung quanh của ống trụ là \({S_{xq}} = 2\pi Rh = 2\pi .\dfrac{2}{\pi }.30 = 120\,\,\left( {c{m^2}} \right)\).
Chọn D.
Câu hỏi 5 :
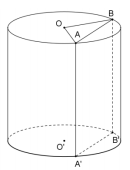
Một hình trụ có diện tích xung quanh là \(4\pi \), thiết diện qua trục là một hình vuông. Một mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo thiết diện \(ABB'A'\), biết một cạnh của thiết diện là một dây của đường tròn đáy của hình trụ và căng một cung \({120^0}\). Diện tích của thiết diện \(ABB'A'\) bằng:
- A \(2\sqrt 3 \)
- B \(2\sqrt 2 \)
- C \(3\sqrt 2 \)
- D \(\sqrt 3 \)
Đáp án: A
Phương pháp giải:
- Diện tích xung quanh của hình trụ có chiều cao \(h\), bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\), từ đó tính \(rh\).
- Áp dụng định lí Côsin trong tam giác tính dây căng cung \({120^0}\). Từ đó tính diện tích thiết diện \(ABB'A'\).
Lời giải chi tiết:
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là \(r,\,\,h\).
Theo bài ra ta có: \({S_{xq}} = 4\pi \Leftrightarrow 2\pi rh = 4\pi \Leftrightarrow rh = 2\).
Xét tam giác \(OAB\) có \(OA = OB = r\), \(\angle AOB = {120^0}\).
Áp dụng định lí Côsin rong tam giác ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \angle AOB\\A{B^2} = {r^2} + {r^2} - 2{r^2}.\dfrac{{ - 1}}{2}\\A{B^2} = 3{r^2}\\ \Rightarrow AB = r\sqrt 3 \end{array}\)
\( \Rightarrow {S_{ABB'A'}} = AB.BB' = r\sqrt 3 .h = \sqrt 3 rh = 2\sqrt 3 \).
Chọn A.
Câu hỏi 6 :
Cho hình trụ có \(O,\,\,O'\) là tâm hai đáy. Xét hình chữ nhật \(ABCD\) có \(A,\,\,B\) cùng thuộc \(\left( O \right)\) và \(C,\,\,D\) cùng thuộc \(\left( {O'} \right)\) sao cho \(AB = a\sqrt 3 \), \(BC = 2a\) đồng thời \(\left( {ABCD} \right)\) tạo với mặt phẳng đáy hình trụ góc \({60^0}\). Thể tích khối trụ bằng:
- A \(\pi {a^3}\sqrt 3 \)
- B \(\dfrac{{\pi {a^3}\sqrt 3 }}{9}\)
- C \(\dfrac{{\pi {a^3}\sqrt 3 }}{3}\)
- D \(2\pi {a^3}\sqrt 3 \)
Đáp án: A
Phương pháp giải:
- Xác định góc giữa mặt \(\left( {ABCD} \right)\) và mặt đáy.
- Sử dụng tỉ số lượng giác của góc nhọn và định lí Pytago tính chiều cao và bán kính đáy của hình trụ.
- Thể tích khối trụ có chiều cao \(h\), bán kính đáy \(r\) là \(V = \pi {r^2}h\).
Lời giải chi tiết:
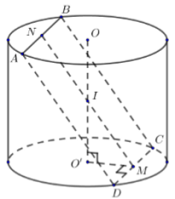
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(CD,\,\,AB\) và \(I\) là trung điểm của \(OO'\).
Ta có:
\(\left\{ \begin{array}{l}\left( {ABCD} \right) \cap \left( {O'CD} \right) = CD\\IM \subset \left( {ABCD} \right),\,\,IM \bot CD\\O'M \subset \left( {O'CD} \right),\,\,O'M \bot CD\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABCD} \right);\left( {O'BC} \right)} \right) = \angle \left( {IM;O'M} \right) = \angle IMO' = {60^0}\).
Ta có: \(MN = BC = 2a\) \( \Rightarrow IM = \dfrac{1}{2}MN = a\).
Xét tam giác vuông \(O'IM\) có: \(O'M = IM.\cos {60^0} = \dfrac{a}{2}\), \(O'I = IM.\sin {60^0} = \dfrac{{a\sqrt 3 }}{2}\).
\( \Rightarrow \) Chiều cao của khối trụ là \(h = OO' = 2O'I = a\sqrt 3 \).
Áp dụng định lí Pytago trong tam giác vuông \(O'CM\) có: \(O'C = \sqrt {O'{M^2} + C{M^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{3{a^2}}}{4}} = a\).
\( \Rightarrow \) Bán kính đáy của khối trụ là \(r = O'C = a\).
Vậy thể tích của khối trụ là: \(V = \pi {r^2}h = \pi .{a^2}.a\sqrt 3 = \pi {a^3}\sqrt 3 \).
Chọn A.
Câu hỏi 7 :
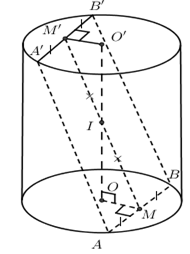
Cho khối trụ có hai đáy là \(\left( O \right)\) và \(\left( {O'} \right)\). \(AB,\,\,CD\) lần lượt là hai đường kính của \(\left( O \right)\) và \(\left( {O'} \right)\), góc giữa \(AB\) và \(CD\) bằng \({30^0}\), \(AB = 6\) và thể tích khối tứ diện \(ABCD\) bằng 30. Thể tích khối trụ đã cho bằng:
- A \(180\pi \)
- B \(90\pi \)
- C \(30\pi \)
- D \(45\pi \)
Đáp án: B
Phương pháp giải:
Gọi \(A',\,\,B'\) lần lượt là hình chiếu của \(A,\,\,B\) lên đường tròn \(\left( O \right)\).
\(C',\,\,D'\) lần lượt là hình chiếu của \(C,\,\,D\) lên đường tròn \(\left( {O'} \right)\).
- Phân chia khối đa diện: \({V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\), chứng minh \({V_{A.A'CD}} = {V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\), từ đó tính \({V_{AC'BD'.A'CB'D}}\).
- Tính diện tích tam giác \(OAC'\), sử dụng công thức \({S_{OAC'}} = \dfrac{1}{2}OA.OC'.\sin \angle AOC'\), từ đó suy ra \({S_{AC'BD'}}\).
- Tính chiều cao \(AA'\): \(AA' = \dfrac{{{V_{AC'BD'.A'CB'D}}}}{{{S_{AC'BD'}}}}\).
- Tính thể tích khối trụ có chiều cao \(h\), bán kính đáy \(r\): \(V = \pi {r^2}h\).
Lời giải chi tiết:
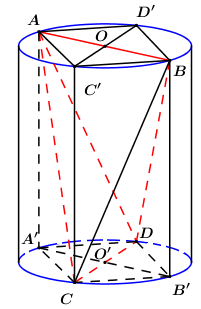
Gọi \(A',\,\,B'\) lần lượt là hình chiếu của \(A,\,\,B\) lên đường tròn \(\left( O \right)\).
\(C',\,\,D'\) lần lượt là hình chiếu của \(C,\,\,D\) lên đường tròn \(\left( {O'} \right)\).
\( \Rightarrow AC'BD'\) là hình bình hành, lại có \(AB = CD = C'D'\) nên \(AC'BD'\) là hình chữ nhật.
Khi đó \(AC'BD'.A'CB'D\) là hình hộp chữ nhật.
Ta có: \({V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\).
Ta có: \({V_{A.A'CD}} = \dfrac{1}{3}AA'.{S_{A'CD}} = \dfrac{1}{3}AA'.\dfrac{1}{2}{S_{A'CB'D}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\).
CMTT ta có: \({V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\).
\(\begin{array}{l} \Rightarrow {V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + 4.\dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\\ \Rightarrow {V_{ABCD}} = \dfrac{1}{3}{V_{AC'BD'.A'CB'D}} = 30\\ \Rightarrow {V_{AC'BD'.A'CB'D}} = 90\end{array}\)
Theo bài ra ta có: \(\angle \left( {AB;CD} \right) = {30^0} \Rightarrow \angle \left( {AB;C'D'} \right) = {30^0}\), giả sử \(\angle \left( {AB;C'D'} \right) = \angle AOC' = {30^0}\).
Lại có \(OA = OC' = \dfrac{1}{2}AB = 3\) \( \Rightarrow {S_{OAC'}} = \dfrac{1}{2}OA.OC'.\sin \angle AOC' = \dfrac{1}{2}.3.3.\sin {30^0} = \dfrac{9}{4}\).
\( \Rightarrow {S_{AC'BD'}} = 4{S_{OAC'}} = 9\).
Ta có: \({V_{AC'BD'.A'CB'D}} = AA'.{S_{AC'BD'}}\)\( \Rightarrow 90 = AA'.9 \Leftrightarrow AA' = 10\).
Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi .O{A^2}.AA' = \pi {.3^2}.10 = 90\pi \).
Chọn B.
Câu hỏi 8 :
Một khối trụ có thể tích bằng \(25\pi \). Nếu chiều cao hình trụ tăng lên 5 lần và giữ nguyên bán kính đáy thì được một hình trụ mới có diện tích xung quanh bằng \(25\pi \). Bán kính đáy của hình trụ ban đầu bằng
- A \(5\)
- B \(15\)
- C \(10\)
- D \(2\)
Đáp án: C
Phương pháp giải:
- Gọi \(h,\,\,r\) lần lượt là chiều cao và bán kính đáy của hình trụ, tính thể tích hình trụ \(V = \pi {r^2}h\,\,\,\left( 1 \right)\).
- Tính chiều cao mới \(h'\) và bán kính mới \(r'\) của hình trụ theo \(h,\,\,r\).
- Tính diện tích xung quanh mới của hình trụ \({S_{xq}}' = 2\pi r'h'\,\,\,\left( 2 \right)\).
- Giải hệ phương trình (1), (2) tìm \(h,\,\,r\).
Lời giải chi tiết:
Gọi \(h,\,\,r\) lần lượt là chiều cao và bán kính đáy của hình trụ, ta có thể tích khối trụ ban đầu là \(V = \pi h{r^2} = 25\pi \Rightarrow h{r^2} = 25\,\,\,\left( 1 \right)\).
Chiều cao mới của hình trụ là \(h' = 5h\), bán kính đáy mới của hình trụ là \(r' = r\).
Khi đó ta có diện tích xung quanh mới của hình trụ là:
\({S_{xq}}' = 2\pi r'.h' = 2\pi r.5h = 25\pi \Rightarrow rh = \dfrac{5}{2}\,\,\,\left( 2 \right)\)
Lấy (1) chia (2) ta có \(r = 10\).
Chọn C.
Câu hỏi 9 :
Cho hình trụ có chiều cao bằng \(6a.\) Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song song với trục và cách trục một khoảng bằng \(3a,\) thiết diện thu được là một hình vuông. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
- A \(216\,\pi {a^3}.\)
- B \(150\pi {a^3}.\)
- C \(54\pi {a^3}.\)
- D \(108\pi {a^3}.\)
Đáp án: D
Phương pháp giải:
Thể tích khối trụ có bán kính đáy \(R\) và chiều cao \(h\) là: \(V = \pi {R^2}h.\)
Lời giải chi tiết:
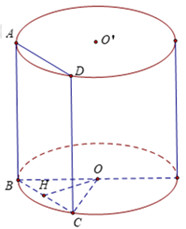
Xét khối trụ như hình vẽ. Ở đó ABCD là hình vuông cạnh \(AB = BC = 6a\)
Gọi H là trung điểm BC thì \(OH \bot BC \Rightarrow OH \bot \left( {ABCD} \right)\)
Mà \(OO'//\left( {ABCD} \right)\) nên \(d\left( {OO',\left( {ABCD} \right)} \right) = d\left( {O,\left( {ABCD} \right)} \right) = OH = 3a\)
Áp dụng định lý Pitago cho tam giác OHB vuông tại H có:
\(OB = \sqrt {O{H^2} + H{B^2}} \) \( = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {3a} \right)}^2}} = 3a\sqrt 2 \)
\( \Rightarrow \) Thể tích khối trụ đã cho là: \(V = \pi .O{B^2}.AB = \pi .{\left( {3a\sqrt 2 } \right)^2}.6a = 108\pi {a^3}.\)
Chọn D.
Câu hỏi 10 :
Cho hình trụ có chiều cao bằng bán kính đáy và bằng \(5cm.\) Mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo một thiết diện có chu vi bằng \(26\,cm.\) Khoảng cách từ \(\left( \alpha \right)\) đến trục của hình trụ bằng:
- A \(4\) cm
- B \(5\) cm
- C \(2\) cm
- D \(3\) cm
Đáp án: D
Phương pháp giải:
Mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo thiết diện là một hình chữ nhật \(ABCD\) với \(AD = BC = h = 5.\)
Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB \Rightarrow OH \bot \left( {ABCD} \right)\) hay \(OH \bot \left( \alpha \right).\)
\( \Rightarrow d\left( {OO';\,\,\left( \alpha \right)} \right) = d\left( {O;\,\,\left( \alpha \right)} \right) = OH.\)
Lời giải chi tiết:
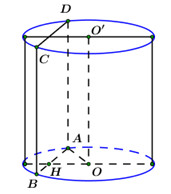
Mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo thiết diện là một hình chữ nhật \(ABCD\) với \(AD = BC = h = 5.\)
\( \Rightarrow 2\left( {AB + BC} \right) = 2\left( {AB + 5} \right) = 26 \Leftrightarrow AB = 8\,\,cm.\)
Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB \Rightarrow OH \bot \left( {ABCD} \right)\) hay \(OH \bot \left( \alpha \right).\)
\( \Rightarrow d\left( {OO';\,\,\left( \alpha \right)} \right) = d\left( {O;\,\,\left( \alpha \right)} \right) = OH.\)
\( \Rightarrow AH = \frac{{AB}}{2} = 4\,\,cm.\)
Áp dụng định lý Pitago cho \(\Delta AOH\) vuông tại \(H\) ta có:
\(\begin{array}{l}OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{5^2} - {4^2}} = 3cm.\\ \Rightarrow d\left( {OO';\,\,\left( \alpha \right)} \right) = 3\,cm.\end{array}\)
Chọn D.
Câu hỏi 11 :
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi bằng 12. Giá trị lớn nhất của thể tích khối trụ bằng
- A \(16\pi .\)
- B \(32\pi .\)
- C \(8\pi .\)
- D \(64\pi .\)
Đáp án: C
Phương pháp giải:
- Gọi \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ. Dựa vào chu vi thiết diện biểu diễn \(h\) theo \(R\).
- Thể tích khối trụ có chiều cao \(h\), bán kính đáy \(R\) là \(V = \pi {R^2}h\).
- Sử dụng BĐT Cô-si: \(abc \le {\left( {\dfrac{{a + b + c}}{3}} \right)^3}\), dấu “=” xảy ra \( \Leftrightarrow a = b = c\).
Lời giải chi tiết:
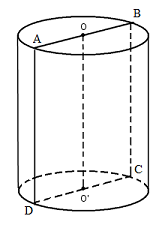
Gọi \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ.
Giả sử thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật \(ABCD\) như hình vẽ, ta có \(AB = 2R\) và \(AD = h\).
Chu vi thiết diện chứa trục bằng 12 \( \Rightarrow 2R + h = 6 \Rightarrow h = 6 - 2R\).
Khi đó thể tích khối trụ:
\(\begin{array}{l}V = \pi {R^2}h = \pi {R^2}\left( {6 - 2R} \right) = \pi .R.R\left( {6 - 2R} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \le \pi .{\left( {\dfrac{{R + R + 6 - 2R}}{3}} \right)^3} = 8\pi \end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(R = 6 - 2R \Leftrightarrow R = 2.\)
Vậy thể tích khối trụ lớn nhất là \(8\pi \) khi \(R = 2\).
Chọn C.
Câu hỏi 12 :
Cho tứ diện đều \(ABCD\) có cạnh bằng \(4\). Hình trụ \(\left( T \right)\) có một đường tròn đáy là đường tròn nội tiếp tam giác \(BCD\) và chiều cao bằng chiều cao của tứ diện \(ABCD\). Diện tích xung quanh của \(\left( T \right)\) bằng:
- A \(\dfrac{{16\sqrt 2 \pi }}{3}\)
- B \(8\sqrt 2 \pi \)
- C \(\dfrac{{16\sqrt 3 \pi }}{3}\)
- D \(8\sqrt 3 \pi \)
Đáp án: A
Phương pháp giải:
- Tính bán kính đường tròn nội tiếp đáy, sử dụng công thức \(r = \dfrac{S}{p}\) trong đó \(S,\,\,p\) lần lượt là diện tích và nửa chu vi của tam giác.
- Sử dụng định lí Pytago tính chiều cao của hình tứ diện.
- Diện tích xung quanh hình trụ có chiều cao \(h\), bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\).
Lời giải chi tiết:
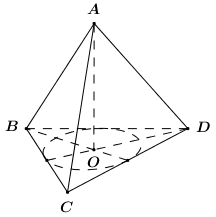
Tam giác \(BCD\) đều cạnh \(a\) nên \({S_{\Delta BCD}} = \dfrac{{{4^2}\sqrt 3 }}{4} = 4\sqrt 3 \).
Gọi \(p\) là nửa chu vi tam giác \(BCD\) ta có \(p = \dfrac{{3.4}}{2} = 6\).
Khi đó bán kính đường tròn nội tiếp tam giác \(BCD\) là \(r = \dfrac{S}{p} = \dfrac{{4\sqrt 3 }}{6} = \dfrac{{2\sqrt 3 }}{3}\), đây cũng chính là bán kính đáy của hình trụ.
Gọi \(O\) là trọng tâm tam giác \(BCD\) ta có \(AO \bot \left( {BCD} \right)\).
Xét tam giác vuông \(SOB\) có; \(BO = \dfrac{2}{3}.\dfrac{{4\sqrt 3 }}{2} = \dfrac{{4\sqrt 3 }}{3}\), \(AB = 4\).
\( \Rightarrow AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {{4^2} - {{\left( {\dfrac{{4\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{4\sqrt 6 }}{3}\), đây cũng chính là chiều cao của hình trụ.
Vậy diện tích xung quanh hình trụ là \({S_{xq}} = 2\pi .\dfrac{{2\sqrt 3 }}{3}.\dfrac{{4\sqrt 6 }}{3} = \dfrac{{16\sqrt 2 \pi }}{3}\).
Chọn A.
Câu hỏi 13 :
Có một khối gỗ là khối lăng trụ đứng \(ABC.A'B'C'\) có \(AB = 30cm,BC = 40cm,CA = 50cm\) và chiều cao \(AA' = 100\,cm.\) Từ khối gỗ này người ta tiện để thu được khối trụ có cùng chiều cao với khối gỗ ban đầu. Thể tích lớn nhất của khối trụ gần nhất với giá trị nào dưới đây?
- A \(62500\,\,c{m^2}.\)
- B \(6000\,\,c{m^2}.\)
- C \(6702\,\,c{m^2}.\)
- D \(6702\,\,c{m^2}.\)
Đáp án: C
Phương pháp giải:
Công thức tính thể tích của khối trụ có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \pi {R^2}h.\)
Lời giải chi tiết:
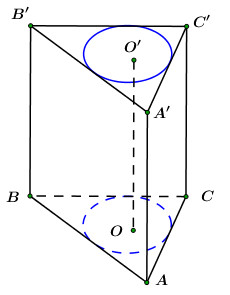
Ta có: \(\left\{ \begin{array}{l}A{B^2} = {30^2} = 900\\B{C^2} = {40^2} = 1600\\A{C^2} = {50^2} = 2500\end{array} \right.\)
\( \Rightarrow C{A^2} = A{B^2} + B{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(B.\)
Khối trụ có thể tích lớn nhất là khối trụ có đường tròn đáy là đường đường tròn nội tiếp tam giác đáy.
Khi đó bán kính đáy của đường tròn đáy là:
\(r = \frac{S}{p} = \frac{{AB.BC}}{{2\left( {AB + BC + AC} \right)}} = \frac{{30.40}}{{2\left( {\frac{{30 + 40 + 50}}{2}} \right)}} = 10\,\,cm.\)
\( \Rightarrow {V_{\max }} = \pi {r^2}h = \pi {.10^2}.100 \approx 31416\,\,c{m^2}.\)
Chọn C.
Câu hỏi 14 :
Cắt một khối trụ cho trước bởi một mặt phẳng vuông góc với trục thì được hai khối trụ mới có tổng diện tích toàn phần nhiều hơn diện tích toàn phần của khối trụ ban đầu \(18\pi \,\,d{m^2}\). Biết chiều cao của khối trụ ban đầu là \(5dm\). Tính tổng diện tích toàn phần \(S\) của hai khối trụ mới.
- A \(S = 48\pi \,\,\left( {d{m^2}} \right)\)
- B \(S = 51\pi \,\,\left( {d{m^2}} \right)\)
- C \(S = 144\pi \,\,\left( {d{m^2}} \right)\)
- D \(S = 66\pi \,\,\left( {d{m^2}} \right)\)
Đáp án: D
Phương pháp giải:
- Phần diện tích toàn phần lớn hơn của 2 khối trụ mới so với khối trụ ban đầu chính là 2 lần diện tích đáy của khối trụ. Từ đó tính được bán kính đáy của khối trụ.
- Diện tích toàn phần của khối trụ có bán kính đáy bằng \(r\) và chiều cao bằng \(h\) là : \({S_{tp}} = 2\pi r\left( {r + h} \right).\)
Lời giải chi tiết:
Gọi bán kính đáy và chiều cao của khối chóp ban đầu lần lượt là \(r,\,\,h\,\,\left( {dm} \right)\,\,\,\left( {r,h > 0} \right).\)
Cắt hình trụ bởi mặt phẳng vuông góc với trục ta được 2 khối trụ mới có tổng chiều cao của 2 khối trụ không thay đổi. Do đó, phần diện tích toàn phần lớn hơn của 2 khối trụ mới với khối trụ ban đầu là phần diện tích đáy mới tạo ra, hay chính là 2 lần diện tích đáy của khối trụ.
Do đó, diện tích đáy của khối trụ là \(9\pi \,\,\left( {d{m^2}} \right)\) hay \(\pi {r^2} = 9\pi \Leftrightarrow r = 3\,\,\left( {dm} \right)\).
Diện tích toàn phần của khối trụ ban đầu là :
\({S_{tp}} = 2\pi r\left( {r + h} \right) = 2.\pi .3\left( {3 + 5} \right) = 48\pi \,\,\left( {d{m^2}} \right)\)
Vậy tổng diện tích toàn phần của 2 khối trụ mới là:
\(S = {S_{tp}} + 18 = 66\pi \,\,\left( {d{m^2}} \right).\)
Chọn D.
Câu hỏi 15 :
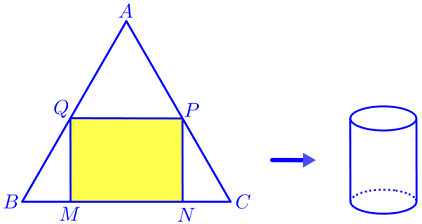
Bạn Bình muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều \(ABC\) có cạnh bằng \(60\left( {cm} \right)\). Bạn muốn cắt mảnh tôn hình chữ nhật \(MNPQ\) từ mảnh tôn nguyên liệu (với \(M,N\) thuộc cạnh \(BC\); \(P,Q\) tương ứng thuộc cạnh \(AC\) và \(AB\)) để tạo thành hình trụ có chiều cao bằng \(MQ\). Thể tích lớn nhất của chiếc thùng mà bạn Bình có thể làm được là:
- A \(\dfrac{{8000\sqrt 3 }}{\pi }\left( {c{m^3}} \right)\)
- B \(\dfrac{{6825}}{{4\pi }}\left( {c{m^3}} \right)\)
- C \(\dfrac{{6825}}{{2\pi }}\left( {c{m^3}} \right)\)
- D \(\dfrac{{4000\sqrt 3 }}{\pi }\left( {c{m^3}} \right)\)
Đáp án: D
Phương pháp giải:
- Đưa độ dài cạnh hình chữ nhật \(MNPQ\) về cùng một biến và tìm điều kiện của biến.
- Hình trụ tạo thành có chiều cao bằng \(MQ\) và chu vi đáy bằng \(MN\).
- Tính thể tích của hình trụ theo biến.
- Bài toán trở thành tìm giá trị lớn nhất của hàm số.
Lời giải chi tiết:
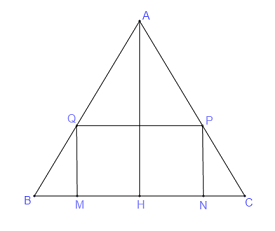
Gọi \(H\) là trung điểm của \(BC\) \( \Rightarrow H\) cũng là trung điểm của \(MN\).
Do \(ABC\) là tam giác đều có cạnh bằng \(60\,\,\left( {cm} \right)\) nên \(\left\{ \begin{array}{l}AH \bot BC\\BH = HC = 30\left( {cm} \right)\\AH = \dfrac{{\sqrt 3 }}{2}.BC = 30\sqrt 3 \left( {cm} \right)\end{array} \right.\)
Đặt \(BM = x\), do \(BM < BH \Rightarrow 0 < x < 30\), ta có :
\(\begin{array}{l}MH = BH - BM = 30 - x\\ \Rightarrow MN = 2MH = 60 - 2x\end{array}\)
\(\left\{ \begin{array}{l}AH \bot BC\\QM \bot MN \Rightarrow QM \bot BC\end{array} \right. \Rightarrow AH\parallel QM\)
\( \Rightarrow \dfrac{{QM}}{{AH}} = \dfrac{{BM}}{{BH}} \Leftrightarrow \dfrac{{QM}}{{30\sqrt 3 }} = \dfrac{x}{{30}}\)\( \Leftrightarrow QM = \sqrt 3 x\) (Định lí Ta-lét)
Gọi \(r\) là bán kính đáy của hình trụ được tạo thành.
Hình trụ được tạo thành có chiều cao bằng \(MQ = \sqrt 3 x\) và chu vi đáy bằng \(MN\) nên :
\(2\pi r = MN \Leftrightarrow 2\pi r = 60 - 2x \Leftrightarrow r = \dfrac{{30 - x}}{\pi }\)
Thể tích của hình trụ được tạo thành từ hình chữ nhật \(MNPQ\) là :
\(\begin{array}{l}V = \pi {r^2}.MQ = \pi .{\left( {\dfrac{{30 - x}}{\pi }} \right)^2}.\sqrt 3 x\\\,\,\,\,\, = \dfrac{{\sqrt 3 x\left( {900 - 60x + {x^2}} \right)}}{\pi }\\\,\,\,\,\, = \dfrac{{\sqrt 3 }}{\pi }\left( {{x^3} - 60{x^2} + 900x} \right)\end{array}\)
Xét hàm số \(f\left( x \right) = {x^3} - 60{x^2} + 900x\) trên khoảng \(\left( {0;30} \right)\) ta có :
\(\begin{array}{l}f'\left( x \right) = 3{x^2} - 120x + 900\\f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 30\,\,\left( {ktm} \right)\\x = 10\,\,\,\left( {tm} \right)\end{array} \right. \Leftrightarrow x = 10\end{array}\)
Ta có BBT như sau :
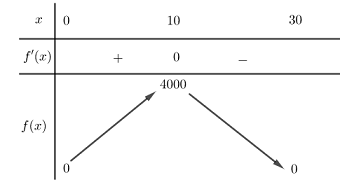
Từ BBT ta thấy \(\mathop {\max }\limits_{\left( {0;30} \right)} f\left( x \right) = f\left( {10} \right) = 4000\).
Do đó, thể tích lớn nhất của hình trụ tạo được là \(\dfrac{{4000\sqrt 3 }}{\pi }\,\,\,\left( {c{m^3}} \right).\)
Chọn D.
Câu hỏi 16 :
Một công ty dự kiến chi 1 tỷ đồng để sản xuất các thùng đựng sơn hình trụ có dung tích 5 lít. Biết rằng chi phí để làm mặt xung quanh của thùng đó là 100.000 đ/m2, chi phí để làm mỗi mặt đáy của thùng là 120.000 đ/\({m^2}\). Hãy tính số thùng sơn tối đa mà công ty đó sản xuất được (Giả sử chi phí cho các mối nối không đáng kể).
- A \(18.209\) thùng.
- B \(57.582\) thùng.
- C \(12.525\) thùng
- D \(58.135\) thùng.
Đáp án: D
Phương pháp giải:
- Khảo sát hàm số.
- Công thức tính thể tích của khối trụ: \(V = \pi {R^2}h\)
Lời giải chi tiết:
Đổi \(5\,l = 5d{m^3} = \dfrac{1}{{200}}{m^3}\).
Giả sử bán kính đáy của hình trụ là \(r\left( m \right)\). Ta có: \(V = \pi {r^2}h = \dfrac{1}{{200}} \Rightarrow h = \dfrac{1}{{200\pi {r^2}}}\left( m \right)\)
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh = 2\pi r.\dfrac{1}{{200\pi {r^2}}} = \dfrac{1}{{100r}}\left( {{m^2}} \right)\)
Diện tích hai đáy của hình trụ là: \({S_d} = 2\pi {r^2}\left( {{m^2}} \right)\)
Chi phí làm 1 chiếc thùng là :
\(T = \dfrac{1}{{100r}}.100 + 2\pi {r^2}.120 = \dfrac{1}{r} + 240\pi {r^2} = \dfrac{1}{{2r}} + \dfrac{1}{{2r}} + 240\pi {r^2}\)\( \ge 3\sqrt[3]{{\dfrac{1}{{2r}}.\dfrac{1}{{2r}}.240\pi {r^2}}} = 3.\sqrt[3]{{60\pi }}\) (nghìn đồng)
Chi phí làm 1 chiếc thùng rẻ nhất là \(3.\sqrt[3]{{60\pi }}\), khi và chỉ khi làm bán kính đáy của nó thỏa mãn :
\(\dfrac{1}{{2r}} = 240\pi {r^2} \Leftrightarrow {r^3} = \dfrac{1}{{480\pi }} \Leftrightarrow r = \dfrac{1}{{\sqrt[3]{{480\pi }}}}\)
Ta có: 1 tỷ : \(3.\sqrt[3]{{60\pi }}\) nghìn đồng \( \approx \)58 135
Vậy số thùng sơn tối đa mà công ty đó sản xuất được \(58 135\) thùng.
Chọn D.
Câu hỏi 17 :
Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng \(6\pi \left( {cm} \right)\) và thiết diện qua trục là một hình chữ nhật có độ dài đường chéo bằng 10(cm).
- A 18\(\pi \left( {c{m^3}} \right).\)
- B 24\(\pi \left( {c{m^3}} \right).\)
- C 48\(\pi \left( {c{m^3}} \right).\)
- D 72\(\pi \left( {c{m^3}} \right).\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức tính chu vi hình tròn để tính bán kính đáy.
Dùng định lí pytago để tính độ dài đường cao.
Lời giải chi tiết:
Chu vi hình tròn: \(2\pi R = 6\pi \Rightarrow R = 3\left( {cm} \right)\)
Vì thiết diện qua trục hình trụ là một hình chữ nhật có độ dài đường chéo là 10cm.
Nên \(h = \sqrt {{{10}^2} - {6^2}} = 8.\)
Do đó thể tích khối trụ là:\(V = \pi {R^2}h = 72\pi \left( {c{m^3}} \right).\)
Chọn D.
Câu hỏi 18 :
Một nhà máy sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dung tích \(1000c{m^3}\). Muốn chi phí nguyên liệu làm vỏ thùng ít nhất tức là diện tích toàn phần của hình trụ là nhỏ nhất thì bán kính nắp đậy bằng:
- A \(\sqrt[3]{{\dfrac{{500}}{\pi }}}cm\)
- B \(\sqrt[3]{{\dfrac{{1000}}{\pi }}}cm\)
- C \(\sqrt {\dfrac{{1000}}{\pi }} cm\)
- D \(\sqrt {\dfrac{{500}}{\pi }} cm\)
Đáp án: A
Phương pháp giải:
Thể tích của hình trụ có bán kính bằng \(r,\) chiều cao bằng \(h\) là: \(V = \pi {r^2}h\)
Diện tích toàn phần của hình trụ trên là \(\)\({S_{tp}} = 2\pi rh + 2\pi {r^2}\)
Áp dụng BĐT \(AM - GM\) để giải bài toán.
Lời giải chi tiết:
Gọi \(r\) là bán kính đáy, \(h\) là chiều cao của thùng sơn đã cho.
Theo giả thiết, thùng sơn có dung tích bằng \(1000c{m^3}\) nên ta có:
\(V = 1000 \Leftrightarrow \pi {r^2}h = 1000\)
Diện tích toàn phần của thùng sơn có nắp đạy là
\({S_{tp}} = 2\pi {r^2} + 2\pi rh\)
Áp dụng BĐT AM – GM ta có:
\({S_{tp}} = \pi .\left( {2{r^2} + rh + rh} \right) \ge \pi .3\sqrt[3]{{2{r^2}.rh.rh}} = 3\pi .\sqrt[3]{{2{r^4}.{h^2}}} = 3\pi .\sqrt[3]{{2.{{\left( {\dfrac{{1000}}{\pi }} \right)}^2}}}\)
Dấu ‘=’ xảy ra khi và chỉ khi \(2{r^2} = rh \Leftrightarrow h = 2r\)
Mà \({r^2}h = \dfrac{{1000}}{\pi } \Rightarrow 2{r^3} = \dfrac{{1000}}{\pi } \Rightarrow r = \sqrt[3]{{\dfrac{{500}}{\pi }}}\)
Vậy để diện tích toàn phần của thùng sơn nhỏ nhất thì \(r = \sqrt[3]{{\dfrac{{500}}{\pi }}}\)
Chọn A.
Câu hỏi 19 :
Một nhà máy dự định sản xuất cốc thủy tinh hình trụ không nắp có thể tích \(50c{m^3}\). Giá nguyên vật liệu làm thành cốc là \(100\) đồng/\(c{m^2}\) và giá nguyên vật liệu làm thành cốc là \(200\) đồng/\(c{m^2}\). Hỏi chi phí nhỏ nhất mua nguyên vật liệu cho một chiếc cốc là bao nhiêu tiền? (xấp xỉ)
- A \(7513\) đồng
- B 10616 đồng
- C 8235 đồng
- D 9466 đồng
Đáp án: A
Phương pháp giải:
Tính chi phí cần bỏ ra để mau nguyên liệu làm cốc.
Áp dụng BĐT \(AM - GM\) để giải bài toán.
Lời giải chi tiết:
Gọi \(r\) là bán kính đáy cốc, \(h\) là chiều cao của cốc thủy tinh cần làm.
Thể tích của cốc là \(50c{m^3}\) nên \(\pi {r^2}h = 50\)
Diện tích xung quanh cái cốc là \({S_{xq}} = 2\pi rh\)
Diện tích đáy cốc là \({S_d} = \pi {r^2}\) (do cốc không nắp)
Do đó, chi phí mua nguyên liệu để làm cốc là :
\(P = 100.2\pi rh + 200.\pi {r^2} = 200\pi .\left( {rh + {r^2}} \right)\)
Áp dụng BĐT AM – GM ta có:
\(P = 200\pi \left( {{r^2} + rh} \right) = 200\pi \left( {{r^2} + \dfrac{{rh}}{2} + \dfrac{{rh}}{2}} \right) \ge 200\pi .3\sqrt[3]{{{r^2}.\dfrac{{rh}}{2}.\dfrac{{rh}}{2}}} = 200\pi .3\sqrt[3]{{{{\left( {\dfrac{{{r^2}h}}{2}} \right)}^2}}} \approx 7513,25\)
Vậy số tiền nhỏ nhất để mua nguyên liệu làm cốc là 7513 đồng.
Chọn A.
Câu hỏi 20 :
Một hình trụ tròn xoay có hai đáy là hai đường tròn \(\left( {O,R} \right)\) và \(\left( {O',R} \right).\) Biết rằng tồn tại dây cung \(AB\) của đường tròn \(\left( {O,R} \right)\)sao cho tam giác \(O'AB\) đều và góc giữa hai mặt phẳng \(\left( {O'AB} \right)\) và mặt phẳng chứa đường tròn \(\left( {O,R} \right)\) bằng \({60^{\rm{o}}}.\) Tính diện tích xung quanh của hình trụ đã cho.
- A \(\dfrac{{6\sqrt 7 \pi {R^2}}}{7}.\)
- B \(2\sqrt 3 \pi {R^2}.\)
- C \(4\pi {R^2}.\)
- D \(\dfrac{{3\sqrt 7 \pi {R^2}}}{7}.\)
Đáp án: D
Phương pháp giải:
- Xác định góc giữa \(\left( {O'AB} \right)\) và \(\left( {OAB} \right)\).
- Đặt \(h = OO'\), áp dụng định lí Pytago và các tỉ số lượng giác của góc nhọn, tính \(h\) theo \(R\).
- Diện tích xung quanh của hình trụ có bán kính đáy \(R\), chiều cao \(h\) là: \({S_{xq}} = \pi {R^2}h\).
Lời giải chi tiết:
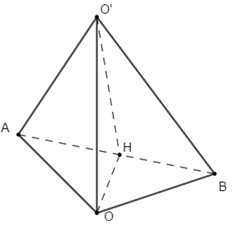
Gọi \(h = OO'\) là chiều cao của hình trụ.
Gọi \(H\) là trung điểm của \(AB\).
Tam giác \(OAB\) cân tại \(O \Rightarrow OH \bot AB\).
Lại có \(OO' \bot AB \Rightarrow O'H \bot AB\).
Ta có: \(\left\{ \begin{array}{l}\left( {O'AB} \right) \cap \left( {OAB} \right) = AB\\\left( {O'AB} \right) \supset O'H \bot AB\\\left( {OAB} \right) \supset OH \bot AB\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {O'AB} \right);\left( {OAB} \right)} \right) = \angle \left( {O'H;OH} \right) = \angle O'HO = {60^0}\).
Xét tam giác vuông \(OO'H\) có: \(O'H = \dfrac{{OO'}}{{\sin {{60}^0}}} = \dfrac{{2h}}{{\sqrt 3 }}\) và \(OH = OO'.\cot {60^0} = \dfrac{h}{{\sqrt 3 }}\).
Tam giasc \(O'AB\) đều nên \(O'H = \dfrac{{O'A\sqrt 3 }}{2}\).
\( \Rightarrow O'A = \dfrac{{2O'H}}{{\sqrt 3 }} = \dfrac{{2.\dfrac{{2h}}{{\sqrt 3 }}}}{{\sqrt 3 }} = \dfrac{{4h}}{3} = AB\).
\( \Rightarrow AH = \dfrac{1}{2}AB = \dfrac{{2h}}{3}\).
Áp dụng định lí Pytago trong tam giác vuông \(OAH\) có:
\(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{{\left( {\dfrac{h}{{\sqrt 3 }}} \right)}^2} + \left( {{{\dfrac{{2h}}{3}}^2}} \right)} = \dfrac{{h\sqrt 7 }}{3} = R\)\( \Leftrightarrow h = \dfrac{{3R}}{{\sqrt 7 }}\).
Vậy diện tích xung quanh của hình trụ là: \({S_{xq}} = \pi {R^2}h = \pi .{R^2}.\dfrac{{3R}}{{\sqrt 7 }} = \dfrac{{3\sqrt 7 \pi {R^3}}}{7}\).
Chọn D.
Câu hỏi 21 :
Gia đình An xây bể hình trụ có thể tích \(150{m^3}.\) Đáy bể làm bằng bê tông giá \(100{\rm{ }}000\)đ/\({m^2}.\) Phần thân làm bằng vật liệu chống thấm giá \(90{\rm{ }}000\) đ/\({m^2},\) nắp bằng nhôm giá \(120{\rm{ }}000\) đ\(/{m^2}.\) Hỏi tỷ số giữa chiều cao bể và bán kính đáy là bao nhiêu để chi phí sản xuất bể đạt giá trị nhỏ nhất
- A \(\dfrac{{31}}{{22}}\).
- B \(\dfrac{{22}}{{31}}\).
- C \(\dfrac{9}{{22}}\).
- D \(\dfrac{{22}}{9}\).
Đáp án: D
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh, diện tích đáy và thể tích của hình trụ chiều cao \(h\), bán kính đáy \(R\) là \({S_{xq}} = 2\pi Rh\), \({S_{day}} = \pi {R^2}\), \(V = \pi {R^2}h\).
Lời giải chi tiết:
Gọi \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ.
Ta có \({S_{xq}} = 2\pi Rh;\) \({S_d} = \pi {R^2};\) \(V = \pi {R^2}h\).
Ta có \(V = 150{m^3} \Rightarrow \pi {R^2}h = 150 \Rightarrow h = \dfrac{{150}}{{\pi {R^2}}}\)
Tổng số tiền để chi trả vật liệu là:
\(\begin{array}{l}\,\,\,\,\,\,\,T = \pi {R^2}.\left( {100 + 120} \right) + 2\pi Rh.90\\ \Leftrightarrow T = 220\pi {R^2} + \dfrac{{2700}}{R}\left( {h = \dfrac{{150}}{{\pi {R^2}}}} \right)\\ \Rightarrow T' = 440\pi R - \dfrac{{2700}}{{{R^2}}} = 0\\ \Leftrightarrow {R^3} = \dfrac{{675}}{{11\pi }}\end{array}\)
Khi đó \(\dfrac{h}{R} = \dfrac{{150}}{{\pi {R^3}}} = \dfrac{{22}}{9}\).
Chọn D.
Câu hỏi 22 :
Trong không gian cho hình vuông \(ABCD\) cạnh \(a\). Gọi \(I\) và \(H\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD\). Khi quay hình vuông \(ABCD\), kể cả các điểm trong nó, xung quanh đường thẳng \(IH\) ta được một khối trụ tròn xoay có thể tích là
- A \(V = \pi {a^3}\)
- B \(V = \dfrac{{\pi {a^3}}}{2}\)
- C \(V = \dfrac{{\pi {a^3}}}{4}\)
- D \(V = \dfrac{{\pi {a^3}}}{3}\)
Đáp án: C
Phương pháp giải:
- Khi quay hình vuông và các điểm bên trong nó xung qunh một đường thẳng đi qua trung điểm 2 cạnh đối diện ta được một hình trụ có chiều cao và đường kính đáy bằng cạnh hình vuông.
- Thể tích của khối trụ có bán kính đáy bằng \(r\) và chiều cao bằng \(h\) là \(V = \pi {r^2}h\).
Lời giải chi tiết:
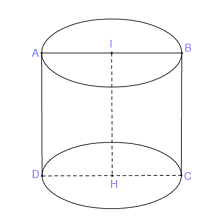
\(I\) và \(H\) là trung điểm của 2 cạnh đối \(AB\) và \(CD\) nên khi quay hình vuông \(ABCD\) và các điểm bên trong nó quanh đường thẳng \(IH\) ta được một khối trụ có chiều cao là \(IH\) và hai đáy có đường kính là \(AB\) và \(CD\).
Do vậy khối trụ trên có chiều cao là \(h = IH = a\) và bán kính đáy là \(r = IA = \dfrac{{AB}}{2} = \dfrac{a}{2}\).
Thể tích của khối trụ tròn xoay tạo thành là :
\(V = \pi .IH.I{A^2} = \pi .a.{\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{\pi {a^3}}}{4}\)
Chọn C.
Câu hỏi 23 :
Khi sản xuất vỏ lon sữa hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ đó bằng 1\(d{m^2}\) và diện tích toàn phần của hình trụ nhỏ nhất thì bán kính đáy của hình trụ phải bằng bao nhiêu ?
- A \(\dfrac{1}{{\sqrt \pi }}dm.\)
- B \(\dfrac{1}{{\sqrt[3]{\pi }}}dm.\)
- C \(\dfrac{1}{{\sqrt[3]{{2\pi }}}}dm.\)
- D \(\dfrac{1}{{\sqrt {2\pi } }}dm.\)
Đáp án: C
Phương pháp giải:
- Áp dụng công thức tính diện tích toàn phần của hình trụ và công thức tính thể tích hình trụ.
- Sử dụng BĐT Cô-si.
Lời giải chi tiết:
Gọi \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao hình trụ.
Ta có \(V = \pi {R^2}h = 1 \Rightarrow h = \dfrac{1}{{\pi {R^2}}}\)
Mặt khác
\(\begin{array}{l}{S_{tp}} = 2\pi {R^2} + 2\pi Rh\\ \Rightarrow {S_{tp}} = 2\pi {R^2} + 2\pi R.\dfrac{1}{{\pi {R^2}}}\\ \Leftrightarrow {S_{tp}} = 2\pi {R^2} + \dfrac{2}{R} = 2\pi {R^2} + \dfrac{1}{R} + \dfrac{1}{R}\end{array}\)
Áp dụng BĐT Cô-si cho 3 số \(2\pi {R^2},\,\,\dfrac{1}{R},\,\,\dfrac{1}{R}\) ta có:
\(2\pi {R^2} + \dfrac{1}{R} + \dfrac{1}{R} \ge 3\sqrt[3]{{2\pi {R^2}.\dfrac{1}{R}.\dfrac{1}{R}}} = 3\sqrt[3]{{2\pi }}\).
\( \Rightarrow {S_{tp}} \ge 3\sqrt[3]{{2\pi }}\).
\( \Rightarrow {S_{tp\,\,\min }} = 3\sqrt[3]{{2\pi }}\). Dấu “=” xảy ra \( \Leftrightarrow 2\pi {R^2} = \dfrac{1}{R} \Leftrightarrow {R^3} = \dfrac{1}{{2\pi }} \Leftrightarrow R = \sqrt[3]{{\dfrac{1}{{2\pi }}}}\,\,\left( {dm} \right)\).
Chọn C.
Câu hỏi 24 :
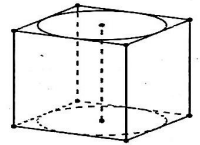
Cho hình lập phương có cạnh bằng 40cm và một hình trụ có đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương (tham khảo hình vẽ bên). Gọi \({S_1};{S_2}\) lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính \(S = {S_1} + {S_2}\left( {c{m^2}} \right)\).
- A \(S = 4\left( {2400 + 3\pi } \right)\)
- B \(S = 2400\left( {4 + 3\pi } \right)\).
- C \(S = 4\left( {2400 + \pi } \right)\)
- D \(S = 2400\left( {4 + \pi } \right)\)
Đáp án: D
Phương pháp giải:
Áp dụng công thức tính diện tích toàn phần của hình lập phương và hình trụ rồi suy ra tổng.
Lời giải chi tiết:
Hình lập phương có cạnh bằng 40cm do đó diện tích toàn phần là \({S_1} = {6.40^2} = 9600\,\,\left( {c{m^2}} \right).\)
Hình trụ có đáy là hình tròn nội tiếp hình vuông cạnh 40cm nên \(r = 20cm\);\(h = 40cm\).
\( \Rightarrow {S_2} = 2\pi {r^2} + 2\pi rh = 2\pi {.20^2} + 2\pi .20.40 = 2400\pi \,\,\left( {c{m^2}} \right).\)
\( \Rightarrow {S_1} + {S_2} = 9600 + 2400\pi = 2400\left( {4 + \pi } \right).\)
Chọn D.
Câu hỏi 25 :
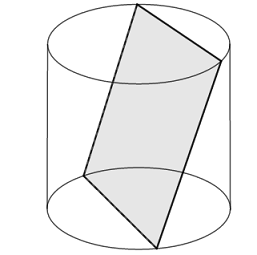
Một chiếc hộp hình trụ với bán kính đáy bằng chiều cao và bằng \(10cm\). Một học sinh bỏ một miếng bìa hình vuông vào chiếc hộp đó và thấy hai cạnh của miếng bìa lần lượt là các dây cung của hai đường tròn đáy hộp và miếng bìa không song song với trục của hộp. Hỏi diện tích của miếng bìa đó bằng bao nhiêu?
- A \(250c{m^2}\)
- B \(200c{m^2}\)
- C \(150c{m^2}\)
- D \(300c{m^2}\)
Đáp án: A
Phương pháp giải:
Khi bỏ miếng bìa hình vuông vào chiếc hộp như giả thiết ta thấy đoạn thẳng nối tâm 2 đáy của chiếc hộp cắt miếng bìa tại trung điểm của nó và là tâm của miếng bìa.
Tính độ dài cạnh của miếng bìa.
Lời giải chi tiết:
Gọi tâm 2 đáy của chiếc hộp hình trụ là \(O\) và \(O'\), miếng bìa hình vuông là \(ABCD\) với \(AB\) là dây cung của đường tròn tâm \(O\) còn \(CD\) là dây cung của đường tròn tâm \(O'\) như trong hình vẽ
Do đặt miếng bìa không song song với trục của hộp nên gọi \(I\)là giao điểm của \(OO'\) và miếng bìa \(ABCD\).
Ta thấy \(I\) chính là trung điểm của \(OO'\) và là tâm của miếng bìa \(ABCD\)
Do đó \(IO = \dfrac{1}{2}OO' = 5\left( {cm} \right);OB = OA = R = 10\left( {cm} \right)\)
\(OO'\) vuông góc với 2 đáy hay \(IO \bot OB\)
Tam giác \(IOB\) vuông tại \(O\) nên \(IB = \sqrt {I{O^2} + O{B^2}} = \sqrt {{5^2} + {{10}^2}} = 5\sqrt 5 \left( {cm} \right)\)
Suy ra \(BD = 2IB = 10\sqrt 5 \left( {cm} \right)\)
Ta có: \(A{D^2} + A{B^2} = B{D^2} \Rightarrow AD = \dfrac{{BD}}{{\sqrt 2 }} = 5\sqrt {10} \left( {cm} \right)\)
Diện tích của miếng bìa hình vuông là \(S = A{D^2} = 250\left( {c{m^2}} \right)\)
Chọn A.
Câu hỏi 26 :
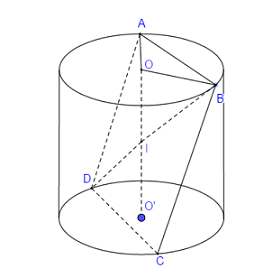
Cho hình trụ có hai đáy là hình tròn \(\left( O \right)\) và \(\left( {O'} \right)\). Trên hai đường tròn đáy lấy hai điểm \(A,B\) sao cho góc giữa \(AB\) và mặt phẳng chứa đường tròn đáy bằng \(45^\circ \) và khoảng cách giữa hai đường thẳng \(AB\) và \(OO'\) bằng \(\dfrac{{a\sqrt 2 }}{2}\). Biết bán kính đáy bằng \(a\), thể tích của khối trụ là
- A \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{2}\)
- B \(V = \pi {a^3}\sqrt 2 \)
- C \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{3}\)
- D \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{6}\)
Đáp án: B
Phương pháp giải:
Khoảng cách giữa hai đường thẳng chéo nhau \(a\) và \(b\) là khoảng cách từ một điểm nằm trên \(a\) đến mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng \(b\) và song song với đường thẳng \(a\)
Tìm góc tạo bởi \(AB\) và mặt phẳng chứa đường tròn đáy.
Tìm đường cao của hình trụ qua khoảng cách giữa \(AB\) và \(OO'\)
Thể tích của khối trụ có bán kính đáy bằng \(a\) và chiều cao bằng \(h\) là \(V = \pi {r^2}h\)
Lời giải chi tiết:
Giả sử \(A\) nằm trên đường tròn tâm \(O,\)\(B\) nằm trên đường tròn tâm \(O'\)
Qua \(A\) kẻ đường thẳng \(AA'//OO'\) (\(A'\) nằm trên đường tròn tâm \(O'\)). Gọi \(I\) là trung điểm của \(A'B\)
\(AA'//OO' \Rightarrow AA' \bot \left( {O'A'B} \right) \Rightarrow AA' \bot O'I\)
Tam giác \(O'A'B\) có \(O'A' = O'B = r\) nên tam giác \(O'A'B\) cân tại \(O'\) hay \(O'I \bot A'B\)
Suy ra \(O'I \bot \left( {A'AB} \right)\)
Do \(AA'//OO'\) nên khoảng cách giữa hai đường thẳng \(AB\) và \(OO'\) là khoảng cách từ \(O'\) đến mặt phẳng \(\left( {AB'A'} \right)\). Hay \(O'I = \dfrac{{a\sqrt 2 }}{2}\)
Ta có: \(IA' = \sqrt {O'A{'^2} - O'{I^2}} = \sqrt {{a^2} - {{\left( {\dfrac{{\sqrt 2 a}}{2}} \right)}^2}} = \dfrac{{\sqrt 2 a}}{2}\)
Góc tạo bởi \(AB\) và mặt phẳng chứa đường tròn đáy là góc giữa \(AB\) và \(A'B\)(do \(AA'\) vuông góc với 2 đáy).
Do đó \(\widehat {ABA'} = 45^\circ \Rightarrow AA' = A'B = 2IA' = \sqrt 2 a\)
Vậy thể tích của hình trụ đã cho bằng \(V = \pi .O{A^2}.AA{'^2} = \pi .{a^2}.\sqrt 2 a = \sqrt 2 \pi {a^3}\)
Chọn B.
Câu hỏi 27 :
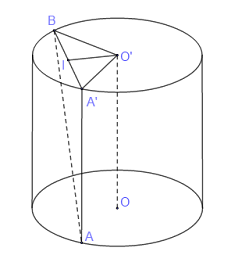
Cho hình trụ có các đáy là đường tròn tâm \(O\) và \(O'\). Đường kính đáy bằng \(6\). Trên đường tròn đáy tâm \(O\) lấy điểm \(A\) sao cho \(AO' = 5\). Diện tích xung quanh hình trụ là?
- A \(24\)
- B \(24\pi \)
- C \(12\pi \)
- D \(24\sqrt 3 \)
Đáp án: B
Lời giải chi tiết:
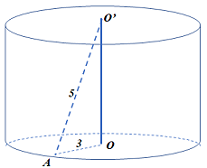
+ Đường kính bằng \(6 \Rightarrow R = OA = 3\).
+ Xét \(\Delta O'OA\)vuông tại \(O\) có
\(O'{O^2} + O{A^2} = O'{A^2} \Leftrightarrow O'{O^2} + {3^2} = {5^2} \Leftrightarrow OO' = 4 = h.\)
+ \({S_{xq}} = 2\pi Rh = 2\pi .3.4 = 24\pi \)
Chọn B
Câu hỏi 28 :
Cho hình trụ có bán kính \(R\). Gọi \(AB,\,\,CD\) lần lượt là hai dây cung song song với nhau và nằm trên hai đường tròn đáy có cùng độ dài là \(R\sqrt 2 \). Mặt phẳng \(\left( {ABCD} \right)\) không song song và cũng không chứa trục của hình trụ. Góc giữa \(\left( {ABCD} \right)\) và đáy bằng \({30^0}\). Tính \(V\) của hình trụ?
- A \(\dfrac{{\pi {R^3}\sqrt 6 }}{3}\)
- B \(\dfrac{{\pi {R^3}\sqrt 6 }}{2}\)
- C \(\dfrac{{\pi {R^3}\sqrt 6 }}{6}\)
- D \(\dfrac{{\pi {R^3}\sqrt 2 }}{3}\)
Đáp án: A
Lời giải chi tiết:
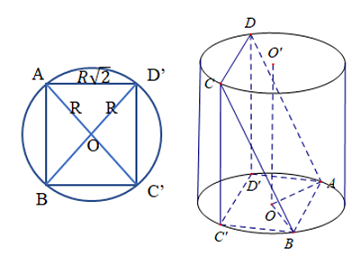
\( + \)Kẻ \(CC'\) vuông đáy tại \(C'\).
\(DD'\) vuông đáy tại \(D'\).
\( \Rightarrow ABC'D'\) là hình bình hành (Do \(CD\parallel C'D'\parallel AB\))
\( + \)\(\Delta OAB\)có: \(O{A^2} + O{B^2} = {R^2} + {R^2} = 2{R^2}\) . Mà\(A{B^2} = 2{R^2}\)
\( \Rightarrow \Delta OAB\)vuông tại \(O\) (Định lí Pytago đảo) \( \Rightarrow AC' \bot BD'\)
\( + \)Ta thấy \(AC' = BD' = 2R\) (Vì tứ giác \(ABC'D'\) nội tiếp đường tròn)
\( \Rightarrow ABC'D'\)là hình vuông \( \Rightarrow AB = AD' = BC' = C'D' = R\sqrt 2 \).
\( + \)Góc \(\left( {ABCD} \right)\) và (đáy) bằng \({30^0} \Rightarrow \widehat {\left( {\left( {ABCD} \right);\left( {day} \right)} \right)} = \widehat {D'AD} = {30^0}\)
\( + \)Xét \({\Delta _v}DAD'\) có: \(\tan {30^0} = \dfrac{{DD'}}{{D'A}} \Rightarrow DD' = R\sqrt 2 .\dfrac{{\sqrt 3 }}{3} = R\dfrac{{\sqrt 6 }}{3}\).
\( \Rightarrow \)Vtrụ \( = \pi {R^2}.\dfrac{{R\sqrt 6 }}{3} = \dfrac{{\pi {R^3}\sqrt 6 }}{3}\).
Chọn A
Câu hỏi 29 :
Cho hình trụ có chiều cao bằng \(6\sqrt 2 cm\). Biết rằng một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song \(AB,\) \(A'B'\) mà \(AB = A'B' = 6cm\), diện tích hình chữ nhật \(ABB'A'\) bằng \(60c{m^2}\). Tính bán kính đáy của hình trụ?
- A \(5cm\)
- B \(3\sqrt 2 cm\)
- C \(4cm\)
- D \(5\sqrt 2 cm\)
Đáp án: C
Phương pháp giải:
Để tính bán kính đường tròn đáy khi đã có độ dài dây cung, ta nên đi tìm khoảng cách từ tâm đến dây cung.
Lời giải chi tiết:
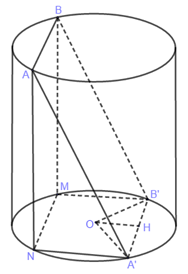
Vẽ một mặt phẳng đi qua \(AB\) và vuông góc với mặt phẳng đáy, cắt mặt đáy còn lại theo dây cung \(MN.\)
Gọi \(O\) là tâm đường tròn đáy chứa dây cung \(A'B'\) , \(H\) là trung điểm \(A'B'\)
Theo giả thiết \(ABB'A'\)là hình chữ nhật nên \(AA' \bot A'B'\) (1)
\(AM\) vuông góc với 2 đáy nên \(AM \bot A'B'\) (2)
Từ (1) và (2) suy ra \(A'B' \bot \left( {AMA'} \right) \Rightarrow A'B' \bot MA'\) . Do đó \(MNB'A'\) là hình chữ nhật.
Diện tích hình chữ nhật \(ABB'A'\) bằng \(60c{m^2}\) nên
\(AA'.A'B' = 60 \Rightarrow AA' = 10\,\,\left( {cm} \right).\)
Chiều cao của khối trụ bằng \(6\sqrt 2 \left( {cm} \right) \Rightarrow AM = 6\sqrt 2 \,\,\left( {cm} \right)\).
Ta có: \(MB' = \sqrt {BB{'^2} - B{M^2}} = \sqrt {{{10}^2} - {{\left( {6\sqrt 2 } \right)}^2}} = 2\sqrt 7 \,\,\left( {cm} \right).\)
Do \(MNB'A'\) là hình chữ nhật nên:
\(R = \dfrac{1}{2}MA' = \dfrac{1}{2}\sqrt {MB{'^2} + A'B{'^2}} = \dfrac{1}{2}\sqrt {{{\left( {2\sqrt 7 } \right)}^2} + {6^2}} = 4\,\,\left( {cm} \right).\)
Vậy bán kính của đường tròn đáy bằng \(4cm\).
Chọn C.
Câu hỏi 30 :
Công ty ông Bình dự định đóng một thùng phi hình trụ (có đáy dưới và nắp đạy phía trên) bằng thép không rỉ để đựng nước. Chi phí trung bình cho \(1{m^2}\) thép không rỉ là \(350.000\)đ. Với chi phí không quá \(6.594.000\)đ, hỏi công ty ông BÌnh có thể có được một thùng phi đựng được tối đa bao nhiêu tấn nước? (Lấy \(\pi = 3,14\)).
- A \(12,56\)
- B \(6,28\)
- C \(3,14\)
- D \(9,52\)
Đáp án: B
Phương pháp giải:
- Diện tích toàn phần của thùng phi là \(S = 2\pi {r^2} + 2\pi rh\).
- Thể tích của thùng phi là \(V = \pi {r^2}h\).
- Kết hợp bất đẳng thức AM – GM để giải bài toán.
Lời giải chi tiết:
Gọi \(r\) là bán kính đáy, \(h\) là chiều cao của thùng phi.
Ta có:
Diện tích toàn thần của thùng phi là \(S = 2\pi {r^2} + 2\pi rh\).
Thể tích của thùng phi là : \(V = \pi {r^2}h\).
Chi phí trung bình cho \(1{m^2}\) thép là \(350000\)đ mà chi phí không được quá \(6594000\) đ nên \(S \le 188,4\left( {{m^2}} \right)\)
Áp dụng bất đẳng thức AM – GM ta có :
\(\begin{array}{l}18,84 \ge S = 2\pi {r^2} + 2\pi rh = \pi \left( {2{r^2} + rh + rh} \right) \ge \pi .3\sqrt[3]{{2{r^2}.rh.rh}} = 3\pi .\sqrt[3]{{2{r^4}{h^2}}}\\ \Rightarrow \sqrt[3]{{2{r^4}{h^2}}} \le \dfrac{{18,84}}{{3\pi }} = 2\\ \Leftrightarrow 2{r^4}{h^2} \le 8\\ \Leftrightarrow {r^4}.{h^2}.{\pi ^2} \le 4{\pi ^2}\\ \Leftrightarrow {V^2} \le 4{\pi ^2}\\ \Rightarrow V \le 2\pi = 6,28\left( {{m^3}} \right)\end{array}\)
Dấu ‘=’ xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}S = 18,84\\2{r^2} = rh\end{array} \right. \Rightarrow \left\{ \begin{array}{l}r = 1\left( m \right)\\h = 2\left( m \right)\end{array} \right.\).
Vậy có thể làm được thùng phi chứa được nhiều nhất là \(6,28\) tấn nước.
Chọn B.
Câu hỏi 31 :
Cắt một hình trụ bằng một mặt phẳng đi qua trục của nó, ta được thiết diện là một hình vuông cạnh \(2a.\) Diện tích xung quanh của hình trụ bằng :
- A \(16\pi {a^2}.\)
- B \(2\pi {a^2}.\)
- C \(8\pi {a^2}.\)
- D \(4\pi {a^2}.\)
Đáp án: D
Phương pháp giải:
Diện tích xung quanh của hình trụ có bán kính đáy \(r\) và đường sinh \(l\) là \({S_{xq}} = 2\pi rl\)
Lời giải chi tiết:
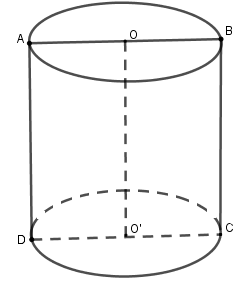
Thiết diện qua trục là hình vuông \(ABCD\) như hình vẽ
Bán kính đáy \(R = \dfrac{{DC}}{2} = \dfrac{{2a}}{2} = a\)
Đường sinh: \(l = BC = 2a\)
Diện tích xung quanh hình trụ: \({S_{xq}} = 2\pi rl = 2\pi .a.2a = 4\pi {a^2}\)
Chọn D.
Câu hỏi 32 :
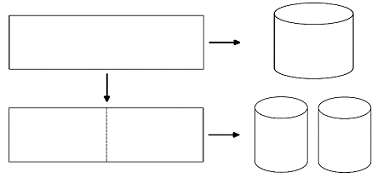
Từ một tấm tôn hình chữ nhật có kích thước \(50cm \times 240cm\), người ta làm các thùng đựng nước hình trụ có chiều cao bằng \(50cm\) theo hai cách sau (xem hình minh họa dưới đây):
* Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng
* Cách 2: Gò tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu \({V_1}\) là thể tích của thùng gò được theo cách 1 và \({V_2}\) là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\)?
- A \(\dfrac{{{V_1}}}{{{V_2}}} = 1\)
- B \(\dfrac{{{V_1}}}{{{V_2}}} = 2\)
- C \(\dfrac{{{V_1}}}{{{V_2}}} = 4\)
- D \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{2}\)
Đáp án: B
Lời giải chi tiết:
Chu vi hình tròn đáy bằng \(240cm \Leftrightarrow 2\pi R = 240 \Leftrightarrow R = \dfrac{{120}}{\pi }\).
Chiều cao hình trụ bằng \(50cm\).
\( \Rightarrow {V_1} = \pi {R^2}h = \pi {\left( {\dfrac{{120}}{\pi }} \right)^2}.50 = \dfrac{{720000}}{\pi }\,\,\left( {c{m^3}} \right)\)
Theo cách 2:
Chu vi hình tròn đáy bằng \(120cm \Leftrightarrow 2\pi R = 120 \Leftrightarrow R = \dfrac{{60}}{\pi }\).
Chiều cao hình trụ bằng \(50cm\).
\({V_2} = {V_1}' + {V_2}' = \pi {r^2}h + \pi {r^2}h = \dfrac{{360000}}{\pi }\).
\( \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{720000}}{\pi }:\dfrac{{360000}}{\pi } = 2.\)
Chọn B
Câu hỏi 33 :
Một hình trụ có tâm các đáy là \(A,\,\,B\). Biết rằng mặt cầu đường kính \(AB\) tiếp xúc với các mặt đáy của hình trụ tại \(A,\,\,B\) và tiếp xúc với mặt phẳng xung quanh của hình trụ đó. Diện tích của mặt cầu này là \(16\pi \). Tính diện tích xung quanh của hình trụ đã cho.
- A \(\dfrac{{16\pi }}{3}\)
- B \(16\pi \)
- C \(8\pi \)
- D \(\dfrac{{8\pi }}{3}\)
Đáp án: B
Lời giải chi tiết:
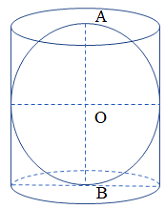
\( + \)Smặt cầu\( = 16\pi \Leftrightarrow 4\pi .O{A^2} = 16\pi \Leftrightarrow OA = 2.\)
\( \Rightarrow AB = h = 2OA = 4.\)
\( + \)Rtrụ\( = OA = 2\)
\( \Rightarrow {S_{xq}} = 2\pi Rl = 2\pi .2.4 = 16\pi .\)
Chọn B
Câu hỏi 34 :
Cho hình trụ có hai đáy là hình tròn \(\left( O \right)\) và \(\left( {O'} \right)\). Trên hai đường tròn lấy hai điểm \(A,\,\,B\) sao cho góc giữa \(AB\) và mặt phẳng chứa đường tròn đáy bằng \({45^0}\) và khoảng cách đến trục \(OO'\) bằng \(\dfrac{{a\sqrt 2 }}{2}\). Biết bán kính đáy bằng \(a\), tính thể tích của khối trụ theo \(a\).
- A \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{6}.\)
- B \(V = \pi {a^3}\sqrt 2 .\)
- C \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{2}.\)
- D \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{3}.\)
Đáp án: B
Lời giải chi tiết:
Đặt \(OO' = h\).
+ Kẻ \(AC\parallel OO' \Rightarrow AC \bot \) (đáy)
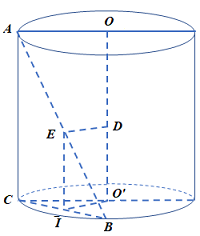
\( \Rightarrow \widehat {(AB,day)} = \widehat {ABC} = {45^0}\)
\( + \) Gọi \(I\) là trung điểm \(BC\).
\( + \) Ta có: \(d\left( {AB;OO'} \right) = d\left( {\left( {ABC} \right),OO'} \right) = d\left( {O',\left( {ABC} \right)} \right) = O'I\)
\( \Rightarrow O'I = \dfrac{{a\sqrt 2 }}{2}\).
\( + \) Vì \(\Delta ABC\) vuông cân tại \(C \Rightarrow BC = AC = h\)
\( + \) Lại có: \(CO{'^2} = C{I^2} + IO{'^2}\)
\( \Leftrightarrow {a^2} = {\left( {\dfrac{{BC}}{2}} \right)^2} + {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} \Rightarrow BC = a\sqrt 2 = h\)
\( + \,\,V = \pi {R^2}h = \pi {a^2}.a\sqrt 2 = \pi {a^3}\sqrt 2 \).
Chọn B
Câu hỏi 35 :
Cho một khối trụ có bán kính đường tròn đáy bằng \(10\). Cắt khối trụ bằng mặt phẳng \(\left( \alpha \right)\) song song với trục ta được thiết diện là hình chữ nhật \(ABCD\) sao cho \(A,\,\,B\) cùng thuộc một đáy của khối trụ và \(AB = 12\). Tính khoảng cách \(h\) từ trục của khối trụ đến mặt phẳng \(\left( \alpha \right)\).
- A \(h = 8\)
- B \(h = \sqrt {44} \)
- C \(h = 10\)
- D \(h = \sqrt {136} \)
Đáp án: A
Lời giải chi tiết:
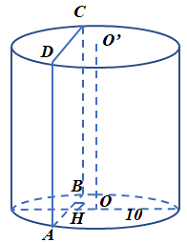
\( + \)Kẻ \(OH \bot AB\)(\(H\) là trung điểm \(AB\))
\( \Rightarrow \)Khoảng cách\(h\) từ trục \({\rm{OO}}'\) tới \(\left( \alpha \right)\)là \(OH\).
+ \(BH = \dfrac{{AB}}{2} = \dfrac{{12}}{2} = 6\)
\( + \) Xét \(\Delta OBH\) vuông tại \(H\) có:
\(O{H^2} = B{O^2} - H{B^2} \Leftrightarrow O{H^2} = {10^2} - {6^2} = 64 \Leftrightarrow OH = 8\)
Chọn A
Câu hỏi 36 :
Chiều cao của khối trụ có thể tích lớn nhất khi nội tiếp trong hình cầu có bán kính \(R\) là
- A \(\dfrac{{R\sqrt 3 }}{3}\)
- B \(\dfrac{{2R\sqrt 3 }}{3}\)
- C \(\dfrac{{4R\sqrt 3 }}{3}\)
- D \(R\sqrt 3 \)
Đáp án: B
Phương pháp giải:
Mặt cầu ngoại tiếp khối trụ có tâm là trung điểm đoạn nối tâm hai đáy của khối trụ
Thể tích của khối trụ được tính bằng công thức: \(V = \pi {r^2}h\) (\(r:\) bán kính đáy, \(h:\) chiều cao của khối trụ)
Tìm mối liên hệ giữa \(r,h,R\) để tìm thể tích lớn nhất của khối trụ
Lời giải chi tiết:
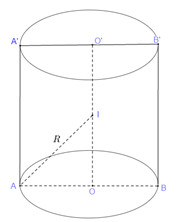
Gọi \(r\) là bán kính đáy, \(h\) là chiều cao của khối trụ đã cho
Gọi \(AB\) là đường kính của mặt đáy tâm \(O,\) \(A'B'\) là đường kính của mặt đáy tâm \(O'\) của hình trụ sao cho \(AA'\) và \(BB'\) vuông góc với mặt phẳng đáy
Gọi \(I\) là trung điểm của \(OO'\) khi đó \(I\) là tâm mặt cầu ngoại tiếp khối trụ trên và \(IA = IB = R\)
Ta có: \(OO' \bot AB \Rightarrow I{O^2} + A{O^2} = I{A^2} \Leftrightarrow \dfrac{{{h^2}}}{4} + {r^2} = {R^2}\)
Thể tích của khối trụ trên là \(V = \pi {r^2}h\) .
Áp dụng bất đẳng thức AM – GM ta có:
\(\begin{array}{l}{R^2} = {r^2} + \dfrac{{{h^2}}}{4} = \dfrac{{{r^2}}}{2} + \dfrac{{{r^2}}}{2} + \dfrac{{{h^2}}}{4} \ge 3\sqrt[3]{{\dfrac{{{r^4}{h^2}}}{{16}}}}\\ \Rightarrow \dfrac{{{r^4}{h^2}}}{{16}} \le {\left( {\dfrac{{{R^2}}}{3}} \right)^3} \Leftrightarrow {r^2}h \le 4\sqrt {\dfrac{{{R^6}}}{{27}}} = \dfrac{{4{R^3}}}{{3\sqrt 3 }}\end{array}\)
\( \Rightarrow V = \pi {r^2}h \le \dfrac{{4\pi {R^3}}}{{3\sqrt 3 }}\)
Dấu ‘=’ xảy ra khi và chỉ khi \(\dfrac{{{r^2}}}{2} = \dfrac{{{h^2}}}{4} = \dfrac{{{R^2}}}{3} \Rightarrow \left\{ \begin{array}{l}r = \dfrac{{\sqrt 6 }}{3}R\\h = \dfrac{{2\sqrt 3 }}{3}R\end{array} \right.\)
Vậy để khối trụ có thể tích lớn nhất thì chiều cao của khối trụ bằng \(\dfrac{{2R\sqrt 3 }}{3}\)
Chọn B.
Câu hỏi 37 :
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi là \(12\,{\rm{cm}}\). Giá trị lớn nhất của thể tích khối trụ là
- A \(32\pi \)\({\rm{c}}{{\rm{m}}^3}\).
- B \(64\pi \)\({\rm{c}}{{\rm{m}}^3}\).
- C \(8\pi \)\({\rm{c}}{{\rm{m}}^3}\).
- D \(16\pi \)\({\rm{c}}{{\rm{m}}^3}\).
Đáp án: C
Phương pháp giải:
+ Sử dụng công thức tính chu vi hình chữ nhật = (chiều dài+chiều rộng).2
+ Sử dụng công thức tính thể tích hình trụ có bán kính đáy \(r\) và chiều cao \(h\) là \(V = \pi {r^2}h\)
+ Sử dụng bất đẳng thức Cô-si cho ba số không âm \(a + b + c \ge 3\sqrt[3]{{abc}}\) để tìm giá trị lớn nhất của thể tích.
Chú ý dấu = xảy ra khi \(a = b = c.\)
(Hoặc sử dụng hàm số để tìm giá trị lớn nhất của thể tích.)
Lời giải chi tiết:
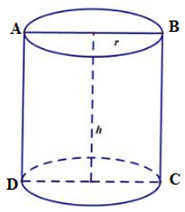
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là \(r\) và \(h\left( {r,h > 0} \right)\)
Thiết diện là hình chữ nhật \(ABCD\) có chu vi \(2\left( {AB + BC} \right) = 2.\left( {h + 2r} \right)\)
Theo giả thiết ta có \(2\left( {h + 2r} \right) = 12 \Leftrightarrow h + 2r = 6 \Rightarrow h = 6 - 2r\,\,\left( {r < 3} \right)\)
Thể tích khối trụ \(V = \pi {r^2}h = \pi {r^2}.\left( {6 - 2r} \right) = \pi r.r.\left( {6 - 2r} \right)\)
Áp dụng BĐT Cô-si cho 3 số \(r;r;6 - 2r\) ta được
\(r + r + 6 - 2r \ge 3\sqrt[3]{{r.r\left( {6 - 2r} \right)}} \Leftrightarrow \sqrt[3]{{r.r\left( {6 - 2r} \right)}} \le 2 \Leftrightarrow {r^2}\left( {6 - 2r} \right) \le 8 \Leftrightarrow \pi {r^2}\left( {6 - 2r} \right) \le 8\pi \)
Hay \(V \le 8\pi \) . Dấu = xảy ra khi \(r = 6 - 2r \Leftrightarrow r = 2\left( {TM} \right)\)
Vậy giá trị lớn nhất của khối trụ là \(V = 8\pi .\)
Chọn C.
Câu hỏi 38 :
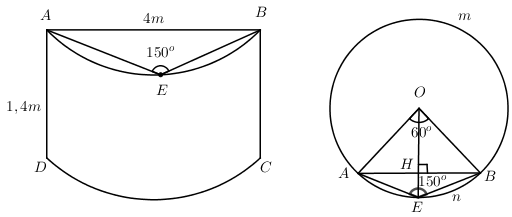
Ông Thành làm lan can ban công nhỏ bằng kính cường lực. Miếng kính này là một phần mặt xung quanh hình trụ như hình vẽ. Miếng kính này là một phần mặt xung quanh hình trụ như hình vẽ. AB = 4m. Góc \(\widehat{AEB}={{150}^{o}}.\) E là trung điểm cung AB. AD = 1,4m. Biết giá thành của phần kính là 500.000 đồng trên \(1{{m}^{2}}\). Số tiền ông thành phải trả là
- A 2.930.000 đồng
- B 3.000.000 đồng
- C 3.200.000 đồng
- D 3.500.000 đồng
Đáp án: A
Lời giải chi tiết:
+) \(\widehat{AEB}={{150}^{o}}\Rightarrow \) Số đo \(\widehat{AmB}={{300}^{o}}\Rightarrow \) Số đo \(\widehat{AnB}={{60}^{o}}\Rightarrow \widehat{AOB}={{60}^{o}}\)
Þ Diện tích phần kính làm ban công bằng \(\frac{1}{6}\) diện tích xung quanh trụ có chiều cao \(h=AD=1,4m\) và đáy là đường tròn (C) bán kính R = OA
+) Trong D cân AOB có: \(\widehat{AOB}={{60}^{o}}\Rightarrow \Delta AOB\,\) đều Þ R = AB = 4
+) Diện tích xung quanh hình trụ là: \({{S}_{xq\,tru}}=C.h=2\pi R.h=2\pi .4.1,4\)
+) Diện tích phần kính: Sphần kính \(=\frac{1}{6}.8\pi .1,4=\frac{5,6\pi }{3}\)
+) Số tiền ông thành phải trả: \(\frac{5,6.3,14}{3}\times 500\,000=2\,930\,000\) (đồng)
Chọn đáp án A
Câu hỏi 39 :
Cho hình trụ có bán kính đáy bằng 4cm. Mặt phẳng (P) không vuông góc với đáy, cắt hai mặt đáy theo dây cung song song với AB và A’B’. AB = A’B’ = 6 cm. Biết \({{S}_{ABB'A'}}=60c{{m}^{2}}.\) Tính chiều cao của hình trụ
- A \(6\sqrt{3}\)
- B \(6\sqrt{2}\)
- C \(6\sqrt{5}\)
- D
\(6\sqrt{7}\)
Đáp án: B
Lời giải chi tiết:
+) Vẽ M, M’ lần lượt là trung điểm của AB, A’B’.
+) Nhận xét: ABA’B’ là hình chữ nhật
+) Diện tích hình chữ nhật ABA’B’: \({{S}_{ABA'B'}}=AB.BB'=60\)
\(\Rightarrow BB'=\frac{60}{AB}=\frac{60}{6}=10cm=MM'\Rightarrow IM=\frac{MM'}{2}=5cm\)
+) Trong tam giác vuông OMA: \(OM=\sqrt{O{{A}^{2}}-M{{A}^{2}}}=\sqrt{{{4}^{2}}-{{3}^{2}}}=\sqrt{16-9}=\sqrt{7}\)
\(\Rightarrow OI=\sqrt{I{{M}^{2}}-O{{M}^{2}}}=\sqrt{{{5}^{2}}-7}=\sqrt{25-7}=\sqrt{18}=3\sqrt{2}\)
+) Chiều cao của hình trụ là: \(h=2OI=2.3\sqrt{2}=6\sqrt{2}\,cm\)
Chọn đáp án B
Câu hỏi 40 :
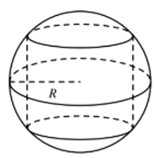
Thể tích lớn nhất của khối trụ nội tiếp hình cầu có bán kính \(R\) bằng:
- A \(\dfrac{{8\pi {R^3}\sqrt 3 }}{9}\)
- B \(\dfrac{{8\pi {R^3}\sqrt 3 }}{3}\)
- C \(\dfrac{{8\pi {R^3}}}{{27}}\)
- D \(\dfrac{{4\pi {R^3}\sqrt 3 }}{9}\)
Đáp án: D
Phương pháp giải:
+) Gọi \(h,\,r\) lần lượt là chiều cao và bán kính đáy của hình trụ.
+) Biểu diễn \(h\) theo \(R,\,\,r\).
+) Sử dụng công thức tính thể tích khối trụ là \(V = \pi {r^2}h\).
+) Sử dụng BĐT Cô-si cho ba số không âm \(\sqrt[3]{{abc}} \le \dfrac{{a + b + c}}{3}\).
Lời giải chi tiết:
Gọi \(h,\,r\) lần lượt là chiều cao và bán kính đáy của hình trụ.
Áp dụng định lí Pytago ta có : \(h = 2\sqrt {{R^2} - {r^2}} \)
Khi đó ta có thể tích khối trụ là \(V = \pi {r^2}h = 2\pi {r^2}\sqrt {{R^2} - {r^2}} = \sqrt 2 \pi \sqrt {{r^4}\left( {{R^2} - {r^2}} \right)} = \sqrt {{r^2}.{r^2}\left( {2{R^2} - 2{r^2}} \right)} \)
Áp dụng BĐT Cô-si ta có : \(\sqrt[3]{{{r^2}.{r^2}\left( {2{R^2} - 2{r^2}} \right)}} \le \dfrac{{{r^2} + {r^2} + \left( {2{R^2} - 2{r^2}} \right)}}{3} = \dfrac{{2{R^2}}}{3} \Rightarrow {r^2}.{r^2}\left( {2{R^2} - 2{r^2}} \right) = \dfrac{{8{R^6}}}{{27}}\)
\( \Rightarrow V \le \sqrt 2 \pi \sqrt {\dfrac{8}{{27}}{R^6}} = \dfrac{{4\pi \sqrt 3 {R^3}}}{9}\). Dấu "=" xảy ra \( \Leftrightarrow {r^2} = 2{R^2} - 2{r^2} \Leftrightarrow r = \dfrac{2}{3}R \Rightarrow \dfrac{{R\sqrt 6 }}{3}\).
Chọn D.
Tổng hợp các bài tập trắc nghiệm mặt trụ mức độ thông hiểu có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm mặt trụ mức độ nhận biết có đáp án và lời giải chi tiết
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục