40 bài tập trắc nghiệm mặt cầu mức độ nhận biết
Làm đề thiCâu hỏi 1 :
Cho khối cầu có bán kính \(R = 6\). Thể tích của khối cầu bằng
- A \(144\pi \).
- B \(36\pi \).
- C \(288\pi \).
- D \(48\pi \).
Đáp án: C
Phương pháp giải:
Thể tích của khối cầu có bán kính R là \(V = \dfrac{4}{3}\pi {R^3}\).
Lời giải chi tiết:
Thể tích của khối cầu bằng \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.6^3} = 288\pi \).
Chọn C.
Câu hỏi 2 :
Cho khối cầu có đường kính bằng 1. Thể tích của khối cầu đã cho bằng
- A \(4\pi \)
- B \(\dfrac{\pi }{6}\)
- C \(\dfrac{{4\pi }}{3}\)
- D \(\dfrac{\pi }{{12}}\)
Đáp án: B
Phương pháp giải:
Thể tích khối cầu có bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\)
Lời giải chi tiết:
Bán kính khối cầu đã cho là: \(R = \dfrac{1}{2}.\)
\( \Rightarrow \) Thể tích khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {\left( {\dfrac{1}{2}} \right)^3} = \dfrac{\pi }{6}.\)
Chọn B.
Câu hỏi 3 :
Cho khối cầu có bán kính bằng 2. Thể tích khối cầu đã cho bằng:
- A \(\dfrac{{32\pi }}{3}\)
- B \(\dfrac{{8\pi }}{3}\)
- C \(\dfrac{{32{\pi ^3}}}{3}\)
- D \(\dfrac{{8{\pi ^3}}}{3}\)
Đáp án: A
Phương pháp giải:
Thể tích khối cầu có bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\)
Lời giải chi tiết:
Thể tích khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}.\)
Chọn A.
Câu hỏi 4 :
Mặt cầu có bán kính bằng 6 thì có diện tích bằng
- A \(72\pi \)
- B \(144\pi \)
- C \(36\pi \)
- D \(288\pi \)
Đáp án: B
Phương pháp giải:
Diện tích mặt cầu bán kính \(r\) là: \(S = 4\pi {r^2}.\)
Lời giải chi tiết:
Diện tích mặt cầu đã cho là:\(S = 4\pi {r^2} = 4\pi {.6^2} = 144\pi .\)
Chọn B.
Câu hỏi 5 :
Một mặt cầu có bán kính bằng \(a.\) Diện tích của mặt cầu đó là:
- A \(\dfrac{{4\pi {a^3}}}{3}\)
- B \(4\pi {a^2}\)
- C \(\dfrac{1}{3}{a^3}\)
- D \({a^2}\)
Đáp án: B
Phương pháp giải:
Diện tích mặt cầu bán kính \(r\) là: \(S = 4\pi {r^2}.\)
Lời giải chi tiết:
Diện tích mặt cầu đã cho là:\(S = 4\pi {a^2}.\)
Chọn B.
Câu hỏi 6 :
Cho khối cầu có đường kính bằng 12. Thể tích khối cầu đã cho bằng
- A \(144\pi \)
- B \(72\pi \)
- C \(48\pi \)
- D \(288\pi \)
Đáp án: D
Phương pháp giải:
Thể tích khối cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}.\)
Lời giải chi tiết:
Bán kính của mặt cầu đã cho là:\(R = 12:2 = 6.\)
Thể tích khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.6^3} = 288\pi .\)
Chọn D.
Câu hỏi 7 :
Một mặt cầu có độ dài đường kính bằng \(4\). Tính diện tích của mặt cầu đó?
- A \(128\pi \).
- B \(64\pi \).
- C \(\dfrac{{64}}{3}\pi \).
- D \(16\pi \).
Đáp án: D
Phương pháp giải:
- Tính bán kính mặt cầu đó.
- Áp dụng công thức tính diện tích mặt cầu bán kính r là: \(S = 4\pi {r^2}.\)
Lời giải chi tiết:
Mặt cầu có đường kính bằng 4 nên bán kính mặt cầu là \(r = 2\).
Khi đó diện tích mặt cầu bằng \(S = 4\pi {r^2} = 4\pi {.2^2} = 16\pi .\)
Chọn D.
Câu hỏi 8 :
Diện tích của mặt cầu bán kính R được xác định theo công thức:
- A \(S = \dfrac{3}{4}\pi {R^2}\)
- B \(S = 2\pi {R^2}\)
- C \(S = 4\pi {R^2}\)
- D \(S = \dfrac{4}{3}\pi {R^2}\)
Đáp án: C
Phương pháp giải:
Diện tích của mặt cầu bán kính R được xác định theo công thức: \(S = 4\pi {R^2}.\)
Lời giải chi tiết:
Diện tích của mặt cầu bán kính R được xác định theo công thức: \(S = 4\pi {R^2}.\)
Chọn C.
Câu hỏi 9 :
Cho khối cầu có đường kính \(d = 3\). Thể tích khối cầu đã cho bằng
- A \(\dfrac{{9\pi }}{4}.\)
- B \(\dfrac{{9\pi }}{2}.\)
- C \(36\pi .\)
- D \(9\pi .\)
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính thể tích khối cầu bán kính \(R\): \(V = \dfrac{4}{3}\pi {R^3}.\)
Lời giải chi tiết:
Ta có khối cầu có đường kính \(d = 3\) nên có bán kính là \(R = \dfrac{d}{2} = \dfrac{3}{2}.\)
Vậy thể tích khối cầu là \(V = \dfrac{4}{3}\pi {\left( {\dfrac{3}{2}} \right)^3} = \dfrac{{9\pi }}{2}.\)
Chọn B.
Câu hỏi 10 :
Cho mặt cầu có bán kính \(R = 3.\) Diện tích của mặt cầu đã cho bằng
- A \(9\pi .\)
- B \(36\pi .\)
- C \(18\pi .\)
- D \(16\pi .\)
Đáp án: B
Phương pháp giải:
Diện tích của mặt cầu bán kính R là: \(S = 4\pi {R^2}\).
Lời giải chi tiết:
Diện tích của mặt cầu đã cho bằng: \(S = 4\pi {R^2} = 4\pi {.3^2} = 36\pi \).
Chọn B.
Câu hỏi 11 :
Thể tích của khối cầu bán kính r là:
- A \(\dfrac{4}{3}\pi {r^3}\)
- B \(\dfrac{4}{3}\pi {r^2}\)
- C \(4\pi {r^2}\)
- D \(2\pi {r^3}\)
Đáp án: A
Phương pháp giải:
Công thức tính thể của khối cầu có bán kính \(r:\;\;V = \dfrac{4}{3}\pi {r^3}.\)
Lời giải chi tiết:
Công thức tính thể của khối cầu có bán kính \(r:\;\;V = \dfrac{4}{3}\pi {r^3}.\)
Chọn A.
Câu hỏi 12 :
Một mặt cầu có bán kính \(R = 4\). Diện tích mặt cầu đó bằng:
- A \(16\pi \)
- B \(\dfrac{{64}}{3}\pi \)
- C \(128\pi \)
- D \(64\pi \)
Đáp án: D
Phương pháp giải:
Diện tích mặt cầu bán kính \(R\) là: \({S_{mc}} = 4\pi {R^2}.\)
Lời giải chi tiết:
Diện tích mặt cầu đó bằng: \(S = 4\pi {.4^2} = 64\pi \).
Chọn D.
Câu hỏi 13 :
Cho khối cầu có thể tích \(36\pi \). Bán kính của khối cầu đã cho bằng:
- A \(2\sqrt 3 \).
- B \(3\sqrt 2 \).
- C \(3\).
- D \(2\).
Đáp án: C
Phương pháp giải:
Thể tích khối cầu có bán kính \(R\) là: \({V_{cau}} = \dfrac{4}{3}\pi {R^3}.\)
Lời giải chi tiết:
Khối cầu có thể tích \(36\pi \)\( \Rightarrow \dfrac{4}{3}\pi {R^3} = 36\pi \Leftrightarrow R = 3.\)
Chọn C.
Câu hỏi 14 :
Cho mặt cầu \(\left( S \right)\) có bán kính \(R = 2\,\,\left( {cm} \right).\) Tính diện tích \(S\) của mặt cầu.
- A \(S = \dfrac{{32\pi }}{3}\,\,c{m^2}\)
- B \(S = 32\pi \,\,c{m^2}\)
- C \(S = 16\pi \,\,c{m^2}\)
- D \(S = \dfrac{{16\pi }}{3}\,\,c{m^2}\)
Đáp án: C
Phương pháp giải:
Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}.\)
Lời giải chi tiết:
Diện tích của mặt cầu đã cho là \(S = 4\pi {R^2} = 4\pi {.2^2} = 16\pi \,\,\left( {c{m^2}} \right).\)
Chọn C.
Câu hỏi 15 :
Diện tích mặt cầu có đường kính \(R\) là:
- A \(\dfrac{4}{3}\pi {R^2}.\)
- B \(\pi {R^2}.\)
- C \(2\pi {R^2}.\)
- D \(4\pi {R^2}.\)
Đáp án: B
Phương pháp giải:
Công thức tính diện tích mặt cầu có bán kính \(r\) là: \(S = 4\pi {r^2}.\)
Lời giải chi tiết:
Diện tích mặt cầu có đường kính \(R\) là: \(S = 4\pi {\left( {\dfrac{R}{2}} \right)^2} = \pi {R^2}.\)
Chọn B.
Câu hỏi 16 :
Một quả bóng đá có dạng hình cầu bán kính 12cm. Diện tích mặt ngoài quả bóng là
- A \(144\pi \left( {c{m^2}} \right).\)
- B \(192\pi \left( {c{m^2}} \right).\)
- C \(576\left( {c{m^2}} \right).\)
- D \(576\pi \left( {c{m^2}} \right).\)
Đáp án: D
Phương pháp giải:
Diện tích khối cầu bán kính \(R\) là \(S = 4\pi {R^2}\).
Lời giải chi tiết:
Diện tích mặt ngoài của quả bóng dạng hình cầu bán kính \(12\,\,cm\) là \(S = 4\pi {.12^2} = 576\pi \,\,\left( {c{m^2}} \right)\).
Chọn D.
Câu hỏi 17 :
Thể tích của khối cầu đường kính 3R bằng:
- A \(\dfrac{{9\pi {R^3}}}{8}\)
- B \(\dfrac{{27\pi {R^3}}}{8}\).
- C \(\dfrac{{9\pi {R^3}}}{2}\).
- D \(36\pi {R^3}\)
Đáp án: C
Phương pháp giải:
Công thức tính thể của khối cầu có bán kính \(r:\;\;V = \dfrac{4}{3}\pi {r^3}.\)
Lời giải chi tiết:
Bán kính khối cầu là: \(r = \dfrac{{3R}}{2}.\)
Thể tích của khối cầu là:\(V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {\left( {\dfrac{{3R}}{2}} \right)^3} = \dfrac{{9\pi {R^3}}}{2}.\)
Chọn C.
Câu hỏi 18 :
Thể tích của khối cầu có bán kính \(6cm\) là
- A \(216\pi \left( {c{m^3}} \right)\)
- B \(288\pi \left( {c{m^3}} \right)\)
- C \(432\pi \left( {c{m^3}} \right)\)
- D \(864\pi \left( {c{m^3}} \right)\)
Đáp án: B
Phương pháp giải:
Thể tích của khối cầu có cạnh bằng \(a\) là \(V = \dfrac{4}{3}\pi {a^3}\)
Lời giải chi tiết:
Thể tích của khối cầu có bán kính \(6cm\) là : \(V = \dfrac{4}{3}\pi {.6^3} = 288\pi \left( {c{m^3}} \right)\)
Chọn B
Câu hỏi 19 :
Một quả bóng bàn có mặt ngoài là mặt cầu đường kính \(4cm.\) Diện tích mặt ngoài quả bóng bàn là
- A \(4\left( {c{m^2}} \right).\)
- B \(16\left( {c{m^2}} \right).\)
- C \(16\pi \left( {c{m^2}} \right).\)
- D \(4\pi \left( {c{m^2}} \right).\)
Đáp án: C
Phương pháp giải:
Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\).
Lời giải chi tiết:
Quả bóng bàn có đường kính 4cm nên có bán kính \(R = 2cm\).
Vậy diện tích mặt cầu là \(S = 4\pi {R^2} = 4\pi {.2^2} = 16\pi \,\,\left( {c{m^2}} \right)\).
Đáp án C.
Câu hỏi 20 :
Tính bán kính của khối cầu có thể tích bằng \(36\pi \left( {c{m^3}} \right)\)?
- A \(6\left( {cm} \right)\)
- B \(3\left( {cm} \right)\)
- C \(9\left( {cm} \right)\)
- D \(\sqrt 6 \left( {cm} \right)\)
Đáp án: B
Phương pháp giải:
Công thức tính thể tích của khối cầu : \(V = \dfrac{4}{3}\pi {R^3}\), \(R\) là bàn kính của khối cầu.
Lời giải chi tiết:
\(V = \dfrac{4}{3}\pi {R^3} \Leftrightarrow 36\pi = \dfrac{4}{3}\pi {R^3} \Leftrightarrow R = 3\,\,\left( {cm} \right)\)
Vậy bán kính của khối cầu đã cho là \(3\left( {cm} \right).\)
Chọn B.
Câu hỏi 21 :
Thể tích của khối cầu có bán kính \(r = 2\) là :
- A \(V = \dfrac{{32\pi }}{3}\)
- B
\(V = \dfrac{{33\pi }}{3}\)
- C \(V = 16\pi \)
- D \(V = 32\pi \)
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính thể tích khối cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\)
Lời giải chi tiết:
Thể tích khối cầu là: \(V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32}}{3}\pi \)
Chọn A
Câu hỏi 22 :
Nếu một mặt cầu có đường kính bằng \(a\) thì có diện tích bằng:
- A \(\pi {a^2}.\)
- B \(4\pi {a^2}.\)
- C \(\frac{4}{3}\pi {a^2}.\)
- D \(\frac{1}{3}\pi {a^2}.\)
Đáp án: A
Phương pháp giải:
Công thức tính diện tích mặt cầu bán kính \(R:\,\,S = 4\pi {R^2}.\)
Lời giải chi tiết:
Bán kính của mặt cầu là:\(r = \frac{a}{2}.\)
\( \Rightarrow \) Diện tích mặt cầu đã cho là: \(S = 4\pi .{\left( {\frac{a}{2}} \right)^2} = \pi {a^2}.\)
Chọn A.
Câu hỏi 23 :
Cho mặt cầu tâm \(O\) đường kính 9cm. Mặt phẳng \(\left( P \right)\) tiếp xúc với mặt cầu đã cho khi và chỉ khi khoảng cách từ \(O\) đến \(\left( P \right)\) bằng:
- A \(3cm.\)
- B \(4,5cm.\)
- C \(9cm.\)
- D \(18cm.\)
Đáp án: B
Phương pháp giải:
\(\left( P \right)\) tiếp xúc với mặt cầu \(\left( S \right)\) tâm \(I\), bán kính \(R \Leftrightarrow d\left( {I;\left( P \right)} \right) = R\).
Lời giải chi tiết:
Mặt cầu tâm \(O\) có đường kính \(9cm \Rightarrow \) Bán kính \(R = \frac{9}{2} = 4,5\,\,\left( {cm} \right)\).
Vì mặt cầu tâm \(\left( P \right)\) tiếp xúc với mặt phẳng \(\left( P \right)\) nên \(d\left( {O;\left( P \right)} \right) = R = 4,5\,\,\left( {cm} \right)\).
Chọn B.
Câu hỏi 24 :
Một khối cầu có bán kính \(2R\) thì có thể tích \(V\) bằng bao nhiêu?
- A \(V = \dfrac{{4\pi {R^3}}}{3}\)
- B \(V = 4\pi {R^2}\)
- C \(V = \dfrac{{32\pi {R^3}}}{3}\)
- D \(V = \dfrac{{24\pi {R^3}}}{3}\)
Đáp án: C
Lời giải chi tiết:
\(V = \dfrac{4}{3}\pi .{\left( {2R} \right)^3} = \dfrac{{32\pi }}{3}.{R^3}\)
Chọn C
Câu hỏi 25 :
Cho hai khối cầu \({S_1}\) và \({S_2}\) có bán kính và thể tích lần lượt là \({R_1},\,\,{R_2}\) và \({V_1},\,\,{V_2}\). Biết \({R_2} = \sqrt 3 {R_1}\), tính \(\dfrac{{{V_2}}}{{{V_1}}}\).
- A \(\sqrt 3 \)
- B \(3\)
- C \(9\)
- D \(3\sqrt 3 \)
Đáp án: D
Lời giải chi tiết:
\(\begin{array}{l}{V_1} = \dfrac{4}{3}\pi R_1^3;\,\,\,\,{V_2} = \dfrac{4}{3}\pi R_2^3\\ \Rightarrow \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{\dfrac{4}{3}\pi R_2^3}}{{\dfrac{4}{3}\pi R_1^3}} = \dfrac{{R_2^3}}{{R_1^3}} = \dfrac{{{{\left( {\sqrt 3 {R_1}} \right)}^3}}}{{R_1^3}} = 3\sqrt 3 \end{array}\)
Chọn D
Câu hỏi 26 :
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = 4\), đường cao \(SH = 3\). Tính bán kính \(r\) của mặt cầu ngoại tiếp hình chóp\(S.ABC\).
- A \(r = 2\).
- B \(r = \dfrac{7}{3}\).
- C \(r = \dfrac{8}{3}\)
- D \(r = 3\).
Đáp án: C
Lời giải chi tiết:
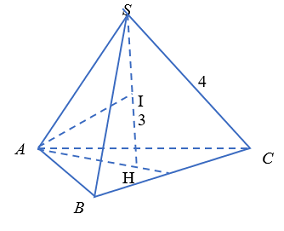
\({R_{mcnt}} = \dfrac{{S{A^2}}}{{2.SH}} = \dfrac{{{4^2}}}{{2.3}} = \dfrac{8}{3}\)
Chọn C
Câu hỏi 27 :
Tính diện tích \(S\) của mặt cầu có đường kính bằng \(6\).
- A \(S = 12\pi \)
- B \(S = 36\pi \)
- C \(S = 48\pi \)
- D \(S = 144\pi \)
Đáp án: B
Phương pháp giải:
Công thức diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\).
Lời giải chi tiết:
Diện tích mặt cầu là \(S = 4\pi .{\left( {\dfrac{6}{2}} \right)^2} = 36\pi \).
Chọn B
Câu hỏi 28 :
Diện tích của mặt cầu đường kính 2a bằng
- A \(\dfrac{{4\pi {a^2}}}{3}\).
- B \(16\pi {a^2}\).
- C \(4\pi {a^2}\).
- D \(\dfrac{{32\pi {a^2}}}{3}\).
Đáp án: C
Phương pháp giải:
Diện tích mặt cầu có bán kính r là \(4\pi {r^2}\).
Lời giải chi tiết:
Diện tích của mặt cầu đường kính 2a bằng \(4\pi {\left( {\dfrac{{2a}}{2}} \right)^2} = 4\pi {a^2}\).
Chọn: C
Câu hỏi 29 :
Hình cầu có đường kính bằng 2 thì thể tích bằng
- A \(\frac{{32}}{3}\pi .\)
- B \(\frac{4}{3}\pi .\)
- C \(4\pi .\)
- D \(16\pi .\)
Đáp án: B
Phương pháp giải:
Thể tích hình cầu bán kính \(R\) là \(V = \frac{4}{3}\pi {R^3}\)
Lời giải chi tiết:
Bán kính hình cầu là \(R = \frac{d}{2} = \frac{2}{2} = 1\)
Thể tích hình cầu là \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \)
Chọn B.
Câu hỏi 30 :
Tính đường kính mặt cầu ngoại tiếp hình lập phương có cạnh bằng \(a\sqrt 3 \).
- A \(3a\)
- B \(a\sqrt 3 \)
- C \(6a\)
- D \(\dfrac{{3a}}{2}\)
Đáp án: A
Phương pháp giải:
- Mặt cầu ngoại tiếp hình lập phương có đường kính là đường chéo chính của hình lập phương.
- Hình lập phương cạnh \(a\) có độ dài đường chéo chính là \(a\sqrt 3 \).
Lời giải chi tiết:
Đường kính mặt cầu ngoại tiếp hình lập phương cạnh \(a\sqrt 3 \) là \(a\sqrt 3 .\sqrt 3 = 3a\).
Chọn A
Câu hỏi 31 :
Diện tích hình cầu bán kính \(a\sqrt 3 \) là
- A \(12{a^2}.\)
- B \(\dfrac{{4\pi {a^2}\sqrt 3 }}{3}.\)
- C \(12\pi {a^2}.\)
- D \(4\pi {a^2}\sqrt 3 .\)
Đáp án: C
Lời giải chi tiết:
Chọn C.
Câu hỏi 32 :
Tính thể tích khối cầu có đường kính \(2a\).
- A \(\frac{{2\pi {a^3}}}{3}.\)
- B \(4\pi {a^2}.\)
- C \(\frac{{4\pi {a^3}}}{3}.\)
- D \(\frac{{4\pi {a^2}}}{3}.\)
Đáp án: C
Phương pháp giải:
Khối cầu có bán kính \(R\) thì có thể tích \(V = \frac{4}{3}\pi {R^3}\)
Lời giải chi tiết:
Bán kính mặt cầu là \(R = 2a:2 = a\)
Thể tích khối cầu là \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {a^3}.\)
Chọn C.
Câu hỏi 33 :
Diện tích của mặt cầu có đường kính 3m là:
- A \(9\pi \left( {{m^2}} \right)\).
- B \(3\pi \left( {{m^2}} \right)\).
- C \(12\pi \left( {{m^2}} \right)\).
- D \(36\pi \left( {{m^2}} \right)\).
Đáp án: A
Phương pháp giải:
Diện tích của mặt cầu có bán kính R là: \(4\pi {R^2}\).
Lời giải chi tiết:
Diện tích của mặt cầu có đường kính 3m là: \(4\pi {\left( {\dfrac{3}{2}} \right)^2} = \)\(9\pi \left( {{m^2}} \right)\).
Chọn: A
Câu hỏi 34 :
Một quả bóng đá có dạng hình cầu bán kính 12cm. Diện tích mặt ngoài quả bóng là
- A \(\frac{{576\pi }}{3}\left( {c{m^2}} \right)\)
- B \(576\left( {c{m^2}} \right)\)
- C \(576\pi \left( {c{m^2}} \right)\)
- D \(144\pi \left( {c{m^2}} \right)\)
Đáp án: C
Phương pháp giải:
Công thức tính diện tích mặt cầu bán kính \(R:\;\;S = 4\pi {R^2}.\)
Lời giải chi tiết:
Ta có: \(S = 4\pi {R^2} = 4\pi {.12^2} = 576\pi \,\,\left( {c{m^2}} \right).\)
Chọn C.
Câu hỏi 35 :
Tính diện tích S của mặt cầu và thể tích V của khối cầu có bán kính bằng 3cm.
- A
\(S = 36\pi \,(c{m^2}){\rm{ v\mu }}V = 36\pi \,(c{m^3}).\)
- B
\(S = 18\pi \,(c{m^2}){\rm{ v\`a }}V = 108\pi \,(c{m^3}).\)
- C
\(S = 36\pi \,(c{m^2}){\rm{ v\`a }}V = 108\pi \,(c{m^3}).\)
- D \(S = 18\pi \,(c{m^2}){\rm{ v\`a }}V = 36\pi \,(c{m^3}).\)
Đáp án: A
Phương pháp giải:
Diện tích mặt cầu bán kính R là: \(S = 4\pi {R^2}\)
Thể tích mặt cầu bán kính R là: \(V = \dfrac{4}{3}\pi {R^3}\)
Lời giải chi tiết:
Diện tích mặt cầu đó là: \(S = 4\pi {.3^2} = 36\pi \left( {c{m^2}} \right)\)
Thể tích mặt cầu đó là: \(V = \dfrac{4}{3}\pi {.3^3} = 36\pi \left( {c{m^3}} \right)\)
Chọn: A
Câu hỏi 36 :
Thể tích khối cầu có bán kính bằng \(\frac{a}{2}\) là:
- A \(\frac{{\pi {a^3}}}{2}\).
- B \(\frac{{\pi {a^2}}}{4}\).
- C \(\frac{{\pi {a^3}}}{6}\).
- D \(\pi {a^2}\).
Đáp án: C
Phương pháp giải:
Công thức tính thể tích khối cầu có bán kính \(r\) là: \(V = \frac{4}{3}\pi {r^3}\).
Lời giải chi tiết:
Thể tích khối cầu có bán kính bằng \(\frac{a}{2}\) là: \(V = \frac{4}{3}\pi {\left( {\frac{a}{2}} \right)^3} = \)\(\frac{{\pi {a^3}}}{6}\).
Chọn: C
Câu hỏi 37 :
Tính diện tích của mặt cầu có bán kính \(r = 2\)
- A \(\dfrac{{32}}{3}\pi \)
- B \(8\pi \)
- C \(32\pi \)
- D \(16\pi \)
Đáp án: D
Phương pháp giải:
Công thức tính diện tích mặt cầu bán kính \(R:\;\;S = 4\pi {R^2}.\)
Lời giải chi tiết:
Công thức tính diện tích mặt cầu bán kính \(r = \;2:\;\;S = 4\pi {.2^2} = 16\pi .\)
Chọn D.
Câu hỏi 38 :
Một mặt cầu có diện tích xung quanh là \(\pi \) thì có bán kính bằng
- A \(\frac{{\sqrt 3 }}{2}\)
- B \(\sqrt 3 \)
- C \(\frac{1}{2}\)
- D \(1\)
Đáp án: C
Phương pháp giải:
Công thức tính diện tích mặt cầu bán kính \(R\) là: \(S = 4\pi {R^2}\).
Lời giải chi tiết:
Ta có: \(S = \pi = 4\pi {R^2} \Leftrightarrow {R^2} = \dfrac{1}{4} \Leftrightarrow R = \dfrac{1}{2}\).
Chọn C.
Câu hỏi 39 :
Một khối cầu có đường kính bằng \(2\sqrt 3 \) có thể tích bằng:
- A \(4\pi \)
- B \(12\pi \)
- C \(4\sqrt 3 \pi \)
- D \(12\sqrt 3 \pi \)
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính thể tích khối cầu \(V = \frac{4}{3}\pi {R^3}\) trong đó R là bán kính khối cầu.
Lời giải chi tiết:
Thể tích khối cầu là \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\frac{{2\sqrt 3 }}{2}} \right)^3} = 4\sqrt 3 \pi \).
Chọn C.
Câu hỏi 40 :
Tập hợp tâm các mặt cầu đi qua ba điểm phân biệt không thẳng hàng là :
- A Một mặt cầu
- B Một đường thẳng
- C Một mặt phẳng
- D Một mặt trụ
Đáp án: B
Phương pháp giải:
Tập hợp tâm các mặt cầu đi qua ba điểm phân biệt A, B, C không thẳng hàng là trục của đường tròn ngoại tiếp tam giác ABC.
Lời giải chi tiết:
Tập hợp tâm các mặt cầu đi qua ba điểm phân biệt A, B, C không thẳng hàng là trục của đường tròn ngoại tiếp tam giác ABC.
Chọn B.
Tổng hợp các bài tập trắc nghiệm mặt cầu mức độ thông hiểu có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm mặt cầu mức độ vận dụng, vận dụng cao có đáp án và lời giải chi tiết
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục









