40 bài tập trắc nghiệm cực trị của hàm số mức độ vận dụng, vận dụng cao
Làm đề thiCâu hỏi 1 :
Biết rằng đồ thị \(\left( H \right):y = \dfrac{{{x^2} + 2x + m}}{{x - 2}}\) (với m là tham số thực) có hai điểm cực trị A, B. Hãy tính khoảng cách từ gốc tọa độ đến đường thẳng AB.
- A \(\dfrac{2}{{\sqrt 5 }}\).
- B \(\dfrac{{\sqrt 5 }}{5}\).
- C \(\dfrac{3}{{\sqrt 5 }}\).
- D \(\dfrac{1}{{\sqrt 5 }}\).
Đáp án: A
Phương pháp giải:
- Tách \(y = \dfrac{{{x^2} + 2x + m}}{{x - 2}} = x + 4 + \dfrac{{m + 8}}{{x - 2}}\) và tính \(y'\).
- Phân tích: \(y = f\left( x \right).y' + g\left( x \right)\), suy ra phương trình đường thẳng đi qua hai điểm cực trị là \(y = g\left( x \right)\).
- Khoảng cách từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(ax + by + c = 0\) là: \(d\left( {M;d} \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có:
\(\begin{array}{l}y = \dfrac{{{x^2} + 2x + m}}{{x - 2}} = x + 4 + \dfrac{{m + 8}}{{x - 2}}\\ \Rightarrow y' = 1 - \dfrac{{m + 8}}{{{{\left( {x - 2} \right)}^2}}}\end{array}\)
Khi đó: \(y = - \left( {x - 2} \right)\left( {1 - \dfrac{{m + 8}}{{{{\left( {x - 2} \right)}^2}}}} \right) + 2x + 2\)\( \Leftrightarrow y = - \left( {x - 2} \right).y' + 2x + 2\).
Giả sử \(A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right)\) là hai điểm cực trị của đồ thị hàm số
\( \Rightarrow \left\{ \begin{array}{l}{y_1} = - \left( {{x_1} - 2} \right).y'\left( {{x_1}} \right) + 2{x_1} + 2 = 2{x_1} + 2\\{y_2} = - \left( {{x_2} - 2} \right).y'\left( {{x_2}} \right) + 2{x_2} + 2 = 2{x_2} + 2\end{array} \right.\)
\( \Rightarrow \) Phương trình đường thẳng đi qua hai điểm cực trị trên là: \(y = 2x + 2 \Leftrightarrow 2x - y + 2 = 0\,\,\left( d \right)\).
Vậy \(d\left( {O;d} \right) = \dfrac{{\left| {2.0 - 0 + 2} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \dfrac{2}{{\sqrt 5 }}.\)
Chọn A.
Câu hỏi 2 :
Cho hàm số \(f\left( x \right) = {x^4} - \left( {2m + 3} \right){x^3} + \left( {m + 5} \right){x^2} \)\(+ \left( {5m - 1} \right)x + 2m - 9\). Có bao nhiêu giá trị nguyên của \(m\) thuộc \(\left[ { - 9;5} \right]\) để hàm số \(y = \left| {f\left( {x + 2020} \right) - 1} \right|\) có số cực trị nhiều nhất.
- A \(8\)
- B \(9\)
- C \(10\)
- D \(11\)
Đáp án: A
Phương pháp giải:
Số điểm cực trị của hàm \(y = \left| {f\left( x \right)} \right|\) với \(f\left( x \right)\) là hàm đa thức = số điểm cực trị của hàm số \(y = f\left( x \right)\) + số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với trục hoành.
Lời giải chi tiết:
Để hàm số \(y = \left| {f\left( {x + 2020} \right) - 1} \right|\) có số cực trị nhiều nhất thì phương trình \(f\left( {x + 2020} \right) - 1 = 0 \Leftrightarrow f\left( {x + 2020} \right) = 1\) có 4 nghiệm phân biệt.
Đặt \(t = x + 2020\), phương trình trở thành \(f\left( t \right) = 1\).
Ta có: \(f\left( t \right) = 1 \Leftrightarrow {t^4} - \left( {2m + 3} \right){t^3} + \left( {m + 5} \right){t^2} + \left( {5m - 1} \right)t + 2m - 9 = 1\)
\(\begin{array}{l} \Leftrightarrow {t^4} - \left( {2m + 3} \right){t^3} + \left( {m + 5} \right){t^2} + \left( {5m - 1} \right)t + 2m - 10 = 0\\ \Leftrightarrow {t^4} - 3{t^3} + 5{t^2} - t - 10 = 2m{t^3} - m{t^2} - 5mt - 2m\\ \Leftrightarrow {t^4} - 3{t^3} + 5{t^2} - t - 10 = m\left( {2{t^3} - {t^2} - 5t - 2} \right)\\ \Leftrightarrow \left( {t + 1} \right)\left( {t - 2} \right)\left( {{t^2} - 2t + 5} \right) = m\left( {t + 1} \right)\left( {t - 2} \right)\left( {2t + 1} \right)\\ \Leftrightarrow \left( {t + 1} \right)\left( {t - 2} \right)\left[ {{t^2} - 2t + 5 - m\left( {2t + 1} \right)} \right] = 0\\ \Leftrightarrow \left( {t + 1} \right)\left( {t - 2} \right)\left[ {{t^2} - 2\left( {m + 1} \right)t - m + 5} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = - 1\\t = 2\\g\left( t \right) = {t^2} - 2\left( {m + 1} \right)t - m + 5 = 0\,\,\,\left( * \right)\end{array} \right.\end{array}\)
Để phương trình \(f\left( {x + 2020} \right) = 1\) có 4 nghiệm phân biệt thì phương trình \(f\left( t \right) = 1\) có 4 nghiệm \(t\) phân biệt, khi đó phương trình (*) cần có 2 nghiệm phân biệt khác \( - 1,\,\,2\).
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\Delta ' > 0\\g\left( { - 1} \right) \ne 0\\g\left( 2 \right) \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 1} \right)^2} - \left( { - m + 5} \right) > 0\\1 + 2\left( {m + 1} \right) - m + 5 \ne 0\\4 - 4\left( {m + 1} \right) - m + 5 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 3m - 4 > 0\\m + 8 \ne 0\\ - 5m + 5 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 1\\m < - 4\end{array} \right.\\m \ne - 8\\m \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 1\\m < - 4\end{array} \right.\\m \ne - 8\end{array} \right.\end{array}\)
Kết hợp điều kiện đề bài \( \Rightarrow m \in \left[ { - 9; - 4} \right) \cup \left( {1;5} \right]\backslash \left\{ { - 8} \right\}\).
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 9; - 7; - 6; - 5;2;3;4;5} \right\}\).
Vậy có 8 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Chọn A.
Câu hỏi 3 :
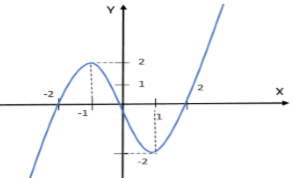
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ. Hàm số \(g\left( x \right) = f\left( {{x^2} - 2} \right)\) có bao nhiêu điểm cực tiểu?
- A \(3\)
- B \(1\)
- C \(5\)
- D \(2\)
Đáp án: A
Phương pháp giải:
- Tính đạo hàm hàm số \(y = g\left( x \right)\).
- Giải phương trình \(g'\left( x \right) = 0\).
- Lập bảng xét dấu \(g'\left( x \right)\).
- Xác định các điểm cực tiểu của hàm số \(g\left( x \right)\): là các điểm mà qua đó \(g'\left( x \right)\) đổi dấu từ âm sang dương.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy: Hàm số có 2 điểm cực trị \(x = - 1,\,\,x = 1\), do đó \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\).
Ta có \(g'\left( x \right) = 2x.f'\left( {{x^2} - 2} \right)\).
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 2} \right) = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 2 = 1\\{x^2} - 2 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 3 \\x = \pm 1\end{array} \right.\) .
Ta có bảng xét dấu \(g'\left( x \right)\) như sau:
![]()
Dựa vào bảng xét dấu ta thấy, \(g'\left( x \right)\) đổi dấu từ âm sang dương khi đi qua các điểm \(x = - \sqrt 3 \), \(x = 0\), \(x = \sqrt 3 \)
Vậy hàm số \(y = g\left( x \right)\) có 3 điểm cực tiểu.
Chọn A.
Câu hỏi 4 :
Cho hàm số \(y = \left( {m + 1} \right){x^3} - 5{x^2} + \left( {6 - m} \right)x + 3\). Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( {\left| x \right|} \right)\) có đúng 5 cực trị?
- A \(6\)
- B \(3\)
- C \(2\)
- D \(5\)
Đáp án: C
Phương pháp giải:
Hàm đa thức:
Số điểm cực trị của hàm số \(y = f\left( {\left| x \right|} \right)\) = 2 \( \times \) Số điểm cực trị dương của \(f\left( x \right)\) + 1.
Lời giải chi tiết:
Để \(y = f\left( {\left| x \right|} \right)\) có đúng 5 cực trị thì hàm số \(y = f\left( x \right)\) có 2 điểm cực trị dương.
\( \Rightarrow \) Phương trình \(y' = 0\) có 2 nghiệm dương phân biệt.
Ta có \(y' = 3\left( {m + 1} \right){x^2} - 10x + 6 - m\).
Để phương trình \(y' = 0\) có 2 nghiệm dương phân biệt thì:
\(\begin{array}{l}\left\{ \begin{array}{l}m + 1 \ne 0\\\Delta ' = 25 - 3\left( {m + 1} \right)\left( {6 - m} \right) > 0\\S = \dfrac{{10}}{{3\left( {m + 1} \right)}} > 0\\P = \dfrac{{6 - m}}{{3\left( {m + 1} \right)}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 1\\3{m^2} - 15m + 7 > 0\\m > - 1\\ - 1 < m < 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > \dfrac{{15 + \sqrt {141} }}{6}\\m < \dfrac{{15 - \sqrt {141} }}{6}\end{array} \right.\\ - 1 < m < 6\end{array} \right. \Leftrightarrow m \in \left( { - 1;\dfrac{{15 - \sqrt {141} }}{6}} \right) \cup \left( {\dfrac{{15 + \sqrt {141} }}{6};6} \right)\end{array}\)
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;5} \right\}\).
Vậy có 2 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Chọn C.
Câu hỏi 5 :
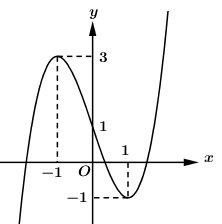
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) với \(a \ne 0\) có đồ thị như hình vẽ sau. Điểm cực đại của đồ thị hàm số \(y = f\left( {4 - x} \right) + 1\) là:
- A \(\left( { - 3;4} \right)\)
- B \(\left( {3;2} \right)\)
- C \(\left( {5;8} \right)\)
- D \(\left( {5;4} \right)\)
Đáp án: D
Phương pháp giải:
- Tính đạo hàm của hàm số \(y = f\left( {4 - x} \right) + 1\).
- Giải phương trình \(y' = 0\).
- Lập BBT hàm số \(y = f\left( {4 - x} \right) + 1\) và kết luận điểm cực đại của hàm số.
Lời giải chi tiết:
Ta có: \(y = f\left( {4 - x} \right) + 1\) \( \Rightarrow y' = - f'\left( {4 - x} \right)\).
\(y' = 0 \Leftrightarrow f'\left( {4 - x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}4 - x = - 1\\4 - x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 3\end{array} \right.\).
Ta có BBT hàm số \(y = f\left( {4 - x} \right) + 1\) như sau:
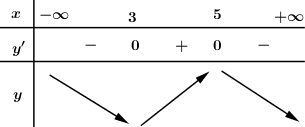
Dựa vào BBT ta có \({x_{CD}} = 5\) \( \Rightarrow {y_{CD}} = f\left( { - 1} \right) + 1 = 3 + 1 = 4\).
Vậy điểm cực đại của đồ thị hàm số \(y = f\left( {4 - x} \right) + 1\) là \(\left( {5;4} \right).\)
Chọn D.
Câu hỏi 6 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \frac{{x\cos x - \sin x}}{{{x^2}}},\forall x \ne 0\). Số điểm cực trị của hàm số đã cho trên khoảng \(\left( {0;100\pi } \right)\) là:
- A \(100\)
- B \(1\)
- C \(99\)
- D \(0\)
Đáp án: C
Phương pháp giải:
Tìm nghiệm của phương trình \(f'\left( x \right) = 0\) trên khoảng \(\left( {0;100\pi } \right)\).
Lời giải chi tiết:
Ta có \(f'\left( x \right) = \frac{{x\cos x - \sin x}}{{{x^2}}} = 0\)
\( \Leftrightarrow x\cos x - \sin x = 0(*)\)
Hàm số (*) có nghiệm khi \({x^2} + 1 \ge 0\) luôn đúng.
Mà \(x \in \left( {0;100\pi } \right)\)\( \Rightarrow x \in \left\{ {\pi ;2\pi ;...;99\pi } \right\}\)
Nên có \(99\) giá trị \(x\) thỏa mãn.
Chọn C.
Câu hỏi 7 :
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để phương trình \(y = \left| {{x^3} - 3x + m} \right|\) có 5 điểm cực trị?
- A \(5\)
- B \(3\)
- C \(1\)
- D vô số
Đáp án: B
Phương pháp giải:
- Dựa vào số điểm cực trị để biện luận nghiệm của phương trình \(y = {x^3} - 3x + m\).
- Lập bảng biếb thiên và suy ra các giá trị của \(m.\)
Lời giải chi tiết:
Để phương trình \(y = \left| {{x^3} - 3x + m} \right|\) có 5 điểm cực trị thì phương trình \({x^3} - 3x + m = 0\) có 3 nghiệm phân biệt.
Ta có: \({x^3} - 3x + m = 0\)\( \Leftrightarrow {x^3} - 3x = - m\).
Đặt \(f\left( x \right) = {x^3} - 3x \Rightarrow f'\left( x \right) = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\)
Bảng biến thiên:
Dựa vào bảng biến thiên ta có \( - 2 < - m < 2 \Leftrightarrow - 2 < m < 2 \Rightarrow m \in \left\{ { - 1;0;1} \right\}\)
Chọn B.
Câu hỏi 8 :
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) (với \(a,\)\(b,\)\(c,\)\(d \in \mathbb{R}\) và \(a \ne 0\)) có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( { - 2{x^2} + 4x} \right)\) là
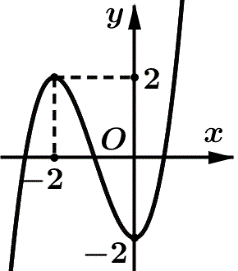
- A \(2.\)
- B \(5.\)
- C \(4.\)
- D \(3.\)
Đáp án: B
Phương pháp giải:
- Tính đạo hàm của hàm số \(g\left( x \right)\).
- Giải phương trình \(g'\left( x \right) = 0\), xác định các nghiệm bội lẻ.
- Số nghiệm bội lẻ của phương trình \(g'\left( x \right) = 0\) là số điểm cực trị của hàm số.
Lời giải chi tiết:
Ta có: \(g'\left( x \right) = \left( { - 4x + 4} \right)f'\left( { - 2{x^2} + 4x} \right)\).
Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l} - 4x + 4 = 0\\ - 2{x^2} + 4x = - 2\\ - 2{x^2} + 4x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 1 \pm \sqrt 2 \\x = 0\\x = 2\end{array} \right.\), các nghiệm này đều là nghiệm đơn.
Do đó \(g'\left( x \right)\) đổi dấu tại đúng 5 điểm trên.
Vậy hàm số \(y = g\left( x \right)\) có 5 điểm cực trị.
Chọn B.
Câu hỏi 9 :
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
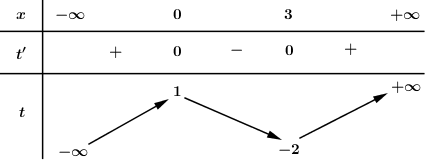
Số điểm cực trị của hàm số \(f\left( {{x^2} - 2x} \right)\) là:
- A \(4\)
- B \(2\)
- C \(5\)
- D \(3\)
Đáp án: D
Phương pháp giải:
Số điểm cực trị của hàm số \(y = f\left( x \right)\) là số nghiệm bội lẻ của phương trình \(g'\left( x \right) = 0\).
Lời giải chi tiết:
Đặt \(g\left( x \right) = f\left( {{x^2} - 2x} \right)\) ta có \(g'\left( x \right) = \left( {2x - 2} \right)f'\left( {{x^2} - 2x} \right)\).
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\f'\left( {{x^2} - 2x} \right) = 0\end{array} \right.\).
Dựa vào BBT ta thấy \(f'\left( {{x^2} - 2x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2x = 0\\{x^2} - 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = 1\\x = - 3\end{array} \right.\)
\( \Rightarrow \) Phương trình \(g'\left( x \right) = 0\) có nghiệm đơn \(x = 0,\,\,x = 2,\,\,x = - 3\), nghiệm bội hai \(x = 1\).
Vậy hàm số đã cho có 3 điểm cực trị.
Chọn D.
Câu hỏi 10 :
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
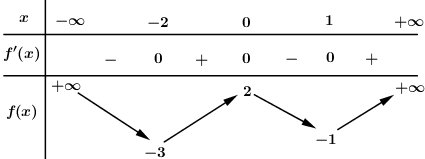
Số điểm cực tiểu của hàm số \(g\left( x \right) = {f^3}\left( x \right) - 3f\left( x \right)\) là:
- A \(6\)
- B \(3\)
- C \(5\)
- D \(4\)
Đáp án: C
Phương pháp giải:
- Tính \(g'\left( x \right)\) và giải phương trình \(g'\left( x \right) = 0\).
- Vẽ phác thảo đồ thị hàm số \(g\left( x \right)\) và suy ra số điểm cực tiểu.
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}g'\left( x \right) = 3{f^2}\left( x \right).f'\left( x \right) - 3f'\left( x \right)\\g'\left( x \right) = 0\\ \Leftrightarrow 3{f^2}\left( x \right).f'\left( x \right) - 3f'\left( x \right) = 0\\ \Leftrightarrow 3f'\left( x \right).\left[ {{f^2}\left( x \right) - 1} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\f\left( x \right) = 1\\f\left( x \right) = - 1\end{array} \right.\end{array}\)
Dựa vào BBT ta thấy:
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\\x = 1\end{array} \right.\), qua các nghiệm này \(f'\left( x \right)\) đều đổi dấu.
\(f\left( x \right) = 1\) có 4 nghiệm phân biệt: \(\left[ \begin{array}{l}x = {x_1} \in \left( { - \infty ; - 2} \right)\\x = {x_2} \in \left( { - 2;0} \right)\\x = {x_3} \in \left( {0;1} \right)\\x = {x_4} \in \left( {1; + \infty } \right)\end{array} \right.\).
\(f\left( x \right) = - 1\) có 3 nghiệm phân biệt \(\left[ \begin{array}{l}x = {x_5} \in \left( { - \infty ; - 2} \right),\,\,{x_5} > {x_1}\\x = {x_6} \in \left( { - 2;0} \right),\,\,{x_6} < {x_2}\\x = 1\end{array} \right.\), trong đó
\(x = 1\) là nghiệm kép.
Suy hàm số \(g\left( x \right)\) có 3 + 4 + 2 = 9 điểm cực trị.
Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } g\left( x \right) = + \infty \) nên số cực tiểu nhiều hơn số cực đại 1 điểm.
Vậy hàm số đã cho có 5 điểm cực tiểu.
Chọn C.
Câu hỏi 11 :
Gọi \(A\left( {{x_1};{y_1}} \right),\,B\left( {{x_2};{y_2}} \right)\) là hai điểm cực trị của đồ thị hàm số \(y = \dfrac{1}{3}{x^3} - 4{x^2} - x + 4\). Tính \(P = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}}\).
- A \(\dfrac{{17}}{3}\).
- B \( - \dfrac{{17}}{3}\).
- C \( - \dfrac{{34}}{3}\).
- D \(\dfrac{{34}}{3}\).
Đáp án: C
Phương pháp giải:
- Viết phương trình đường thẳng qua hai cực trị: Tính \(y'\), lấy y chia cho y’ và lấy phần dư.
- Tính \({y_1}\) theo \({x_1}\), \({y_2}\) theo \({x_2}\) .
- Thay vào biểu thức và rút gọn.
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} - 8x - 1\)
Lấy \(y\) chia cho \(y'\) ta có: \(y = \left( {\dfrac{1}{3}x - \dfrac{4}{3}} \right).y' - \dfrac{{34}}{3}x + \dfrac{8}{3}\)
Ta có: \(A\left( {{x_1};{y_1}} \right),\,B\left( {{x_2};{y_2}} \right)\) là hai điểm cực trị \(y'\left( {{x_1}} \right) = y'\left( {{x_2}} \right) = 0 \Rightarrow \left\{ \begin{array}{l}{y_1} = - \dfrac{{34}}{3}{x_1} + \dfrac{8}{3}\\{y_2} = - \dfrac{{34}}{3}{x_2} + \dfrac{8}{3}\end{array} \right.\)
Khi đó ta có: \(P = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}} = \dfrac{{ - \dfrac{{34}}{3}{x_1} + \dfrac{8}{3} + \dfrac{{34}}{3}{x_2} - \dfrac{8}{3}}}{{{x_1} - {x_2}}} = \dfrac{{ - \dfrac{{34}}{3}\left( {{x_1} - {x_2}} \right)}}{{{x_1} - {x_2}}} = - \dfrac{{34}}{3}\)
Chọn C.
Câu hỏi 12 :
Có tất cả bao nhiêu giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \dfrac{2}{3}{x^3} - m{x^2} - 2\left( {3{m^2} - 1} \right)x + \dfrac{2}{3}\) có hai điểm cực trị có hoành độ \({x_1},{x_2}\)sao cho \({x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) = 1\).
- A \(1\).
- B \(0\).
- C \(3\) .
- D \(2\).
Đáp án: A
Phương pháp giải:
- Tìm đạo hàm của hàm số.
- Tìm điều kiện để hàm số có 2 điểm cực trị: Phương trình \(y' = 0\) có hai nghiệm phân biệt.
- Sử dụng định lí Viét để tìm mối quan hệ giữa hai cực trị \({x_1};\,\,{x_2}\) của hàm số.
- Dựa vào dữ kiện đề bài để tìm m.
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
Ta có hàm số \(y = \dfrac{2}{3}{x^3} - m{x^2} - 2\left( {3{m^2} - 1} \right)x + \dfrac{2}{3}\) có đạo hàm là \(y' = 2{x^2} - 2mx - 2\left( {3{m^2} - 1} \right)\)
Cho \(y' = 0 \Leftrightarrow 2{x^2} - 2mx - 2\left( {3{m^2} - 1} \right) = 0\) \( \Leftrightarrow {x^2} - mx - 3{m^2} + 1 = 0\) (1)
Để hàm số có 2 điểm cực trị thì phương trình (1) phải có 2 nghiệm phân biệt.
Phương trình (1) có hai nghiệm khi và chỉ khi \(\Delta = {m^2} + 3{m^2} - 1 > 0 \Leftrightarrow 4{m^2} - 1 > 0 \Leftrightarrow \left[ \begin{array}{l}m > \dfrac{1}{2}\\m < - \dfrac{1}{2}\end{array} \right.\)
Khi đó hai điểm cực trị \({x_1},\,\,{x_2}\) của hàm số chính là hai nghiệm phân biệt của phương trình (1). Áp dụng định lý Viét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = 1 - 3{m^2}\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) = 1\\ \Leftrightarrow 1 - 3{m^2} + 2m = 1\\ \Leftrightarrow 3{m^2} - 2m = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\,\,\,\,\left( {ktm} \right)\\m = \dfrac{2}{3}\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Chọn A.
Câu hỏi 13 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như sau:
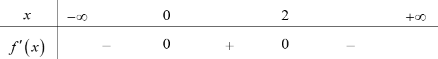 Tổng giá trị tất cả các điểm cực trị của hàm số \(y = f\left( {x - 2019} \right) + 2020\) là:
Tổng giá trị tất cả các điểm cực trị của hàm số \(y = f\left( {x - 2019} \right) + 2020\) là:
- A \(4040\)
- B \(6080\)
- C \(2\)
- D \(2021\)
Đáp án: A
Phương pháp giải:
Dựa vào BBT, tìm khoảng biến thiên của hàm số \(y = f\left( x \right)\)
Từ đó khảo sát hàm số \(y = f\left( {x - 2019} \right) + 2020\)
Lời giải chi tiết:
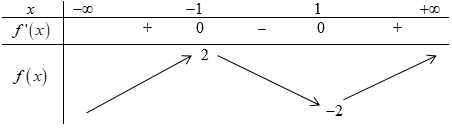
Dựa vào BBT ta thấy hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {0;\,2} \right)\) và nghịch biến trên \(\left( { - \infty ;\,\,0} \right),\,\,\left( {2; + \infty } \right).\)
Hàm số \(y = f\left( x \right)\) có hai điểm cực trị là: \(x = 0,\,\,x = 2.\)
Xét hàm số \(y = f\left( {x - 2019} \right) + 2020\) ta có:
\(\begin{array}{l}y' = f'\left( {x - 2019} \right) \Rightarrow y' = 0 \Leftrightarrow f'\left( {x - 2019} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2019 = 0\\x - 2019 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2019\\x = 2021\end{array} \right.\end{array}\)
Ta có BXD:
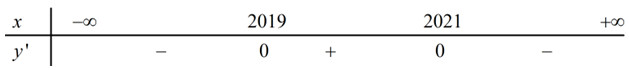
\( \Rightarrow \) Hàm số \(y = f\left( {x - 2019} \right) + 2020\) có hai điểm cực trị là \(x = 2019,\,\,\,x = 2020\)
\( \Rightarrow 2019 + 2021 = 4040.\)
Chọn A.
Câu hỏi 14 :
Cho \(y = \left( {m - 3} \right){x^3} + 2\left( {{m^2} - m - 1} \right){x^2} + \left( {m + 4} \right)x - 1\). Gọi \(S\) là tập tất cả các giá trị nguyên dương của \(m\) để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục \(Oy\). Hỏi \(S\) có bao nhiêu phần tử ?
- A \(4\)
- B \(3\)
- C \(2\)
- D \(1\)
Đáp án: C
Phương pháp giải:
- Gọi số tạo thành có dạng \(x = \overline {abc} \), với \(a\), \(b\), \(c\) đôi một khác nhau và lấy từ \(A\).
- Chọn vị trí cho chữ số 3.
- Chọn 2 chữ số còn lại. Áp dụng quy tắc nhân.
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
Ta có \(y' = 3\left( {m - 3} \right){x^2} + 4\left( {{m^2} - m - 1} \right)x + m + 4\)
Xét \(y' = 0\)\( \Leftrightarrow 3\left( {m - 3} \right){x^2} + 4\left( {{m^2} - m - 1} \right)x + m + 4 = 0\).
Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục \(Oy\) thì phương trình \(y' = 0\) có hai nghiệm phân biệt trái dấu.
Suy ra \(\left\{ \begin{array}{l}3\left( {m - 3} \right) \ne 0\\3\left( {m - 3} \right).\left( {m + 4} \right) < 0\end{array} \right. \Leftrightarrow - 4 < m < 3\).
Mà \(m \in \mathbb{Z},\,\,m > 0\) nên \(m = \left\{ {1;2} \right\}\).
Vậy \(S\) có \(2\) phần tử.
Chọn C.
Câu hỏi 15 :
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), có 3 cực trị và có đồ thị như hình vẽ.
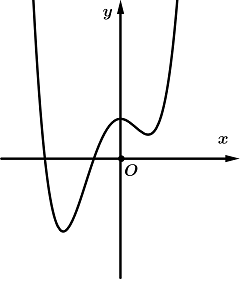
Tìm số điểm cực trị của hàm số \(y = f\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)\).
- A \(3.\)
- B \(0.\)
- C \(1.\)
- D \(2.\)
Đáp án: D
Phương pháp giải:
Tính \(\left[ {f\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)} \right]'\) và tìm số nghiệm bội lẻ, từ đó suy ra số cực trị.
Lời giải chi tiết:
Ta có:
\(g'\left( x \right) = \left[ {f\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)} \right]' = \left[ {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right]'.f'\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)\)\( = - \dfrac{2}{{{{\left( {x - 1} \right)}^3}}}.f'\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow f'\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}\dfrac{1}{{{{\left( {x - 1} \right)}^2}}} = {x_1} < 0\left( {VN} \right)\\\dfrac{1}{{{{\left( {x - 1} \right)}^2}}} = {x_2} = 0\left( {VN} \right)\\\dfrac{1}{{{{\left( {x - 1} \right)}^2}}} = {x_3} > 0\end{array} \right.\)\( \Leftrightarrow x - 1 = \pm \sqrt {\dfrac{1}{{{x_3}}}} \Leftrightarrow x = 1 \pm \sqrt {\dfrac{1}{{{x_3}}}} \) (nghiệm đơn)
Vậy hàm số đã cho có \(2\) điểm cực trị.
Chọn D.
Câu hỏi 16 :
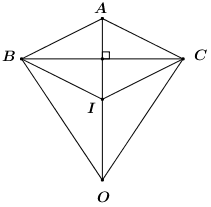
Có bao nhiêu giá trị của tham số \(m\) để đồ thị hàm số \(y = {x^4} - 2m{x^2} + 2\) có ba cực trị \(A,\,\,B,\,\,C\) và ba điểm cực trị này cùng với gốc tọa độ \(O\) thuộc một đường tròn.
- A \(3\)
- B \(2\)
- C \(1\)
- D \(4\)
Đáp án: B
Phương pháp giải:
- Xác định các điểm cực trị của đồ thị hàm số.
- Giả sử \(O,\,\,A,\,\,B,\,\,C\) cùng thuộc đường tròn tâm \(I\), chứng minh \(I\) là trung điểm của \(OA\).
- Chứng minh điều kiện để \(O,\,\,A,\,\,B,\,\,C\) cùng thuộc đường tròn là \(AB \bot OB\).
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
Ta có \(y' = 4{x^3} - 4mx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = m\end{array} \right.\)
Để đồ thị hàm số có 3 điểm cực trị thì phương trình \({x^2} = m\) có 2 nghiệm phân biệt khác 0 \( \Rightarrow m > 0\).
Khi đó \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 2\\x = \sqrt m \Rightarrow y = - {m^2} + 2\\x = - \sqrt m \Rightarrow y = - {m^2} + 2\end{array} \right.\)
Đồ thị hàm số có 3 điểm cực trị
\(A\left( {0;2} \right),\,\,B\left( {\sqrt m ; - {m^2} + 2} \right),\,\,C\left( { - \sqrt m ; - {m^2} + 2} \right)\).
Ta có \(B,\,\,C\) đối xứng qua trục \(Oy\), \(O,\,\,A \in Oy\), do đó \(B,\,\,C\) đối xứng \(OA\).
Giả sử \(O,\,\,A,\,\,B,\,\,C\) cùng thuộc đường tròn tâm \(I\) ta có \(IA = IB = IC = IO\).
\(IB = IC \Rightarrow I\) thuộc trung trực của \(BC \Rightarrow I \in OA\).
\(IO = IA \Rightarrow I\) là trung điểm của \(OA\).
Khi đó ta có \(IB = IA = IO = \frac{1}{2}OA\) \( \Rightarrow \Delta OAB\) vuông tại \(B\) (Định lí đường trung tuyến).
Ta có: \(\overrightarrow {BA} = \left( { - \sqrt m ;{m^2}} \right);\,\,\overrightarrow {BO} = \left( { - \sqrt m ;{m^2} - 2} \right)\).
\(\begin{array}{l}\overrightarrow {BA} .\overrightarrow {BO} = 0\\ \Leftrightarrow m + {m^2}\left( {{m^2} - 2} \right) = 0\\ \Leftrightarrow {m^4} - 2{m^2} + m = 0\\ \Leftrightarrow m\left( {{m^3} - 2m + 1} \right) = 0\\ \Leftrightarrow m\left( {m - 1} \right)\left( {{m^2} + m - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {ktm} \right)\\m = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\m = \dfrac{{ - 1 + \sqrt 5 }}{2}\,\,\,\,\,\,\,\left( {tm} \right)\\m = \dfrac{{ - 1 - \sqrt 5 }}{2}\,\,\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy có 2 giá trị thực của tham số \(m\) thỏa mãn yêu cầu bài toán.
Chọn B.
Câu hỏi 17 :
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} + x} \right)\left( {{x^2} - 3x - 4} \right)\). Gọi \(T\) là tập hợp các giá trị nguyên của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {{x^2} - 6x + 2m} \right)\) có đúng 5 cực trị. Tính tổng \(S\) các phần tử của tập hợp \(T\), biết \(m \in \left( { - 19;20} \right]\).
- A \(S = 200\)
- B \(S = - 161\)
- C \(S = 189\)
- D \(S = 150\)
Đáp án: B
Phương pháp giải:
- Tính đạo hàm của hàm số \(g\left( x \right)\).
- Tìm điều kiện để phương trình \(g'\left( x \right) = 0\) có 5 nghiệm bội lẻ phân biệt.
Lời giải chi tiết:
Ta có: \(f'\left( x \right) = 0 \Leftrightarrow {\left( {x + 1} \right)^2}x\left( {x - 4} \right)\).
Xét hàm số \(y = g\left( x \right)\) có: \(g'\left( x \right) = \left( {2x - 6} \right)f'\left( {{x^2} - 6x + 2m} \right)\).
\( \Rightarrow g'\left( x \right) = \left( {2x - 6} \right){\left( {{x^2} - 6x + 2m + 1} \right)^2}\left( {{x^2} - 6x + 2m} \right)\left( {{x^2} - 6x + 2m - 4} \right)\)
\(g'\left( x \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 3\\{x^2} - 6x + 2m = 0\\{x^2} - 6x + 2m = 4\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\{x^2} - 6x + 2m = 0\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} - 6x + 2m - 4 = 0\,\,\,\left( 2 \right)\end{array} \right.\) .
(Ta không xét phương trình \({x^2} - 6x + 2m = - 1\) vì qua các nghiệm của phương trình này \(g'\left( x \right)\) không đổi dấu).
Để hàm số \(y = g\left( x \right)\) có đúng 5 điểm cực trị thì phương trình (1) và (2), mỗi phương trình có 2 nghiệm phân biệt khác 3.
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta {'_1} = 9 - 2m > 0\\{\Delta _2}' = 9 - 2m + 4 > 0\\ - 9 + 2m \ne 0\\ - 8 + 2m - 4 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m < \frac{9}{2}\\m < \frac{{13}}{2}\end{array} \right. \Leftrightarrow m < \frac{9}{2}\).
Kết hợp điều kiện \( \Rightarrow \left\{ \begin{array}{l}m \in \mathbb{Z}\\m \in \left( { - 19;\frac{9}{2}} \right)\end{array} \right.\) \( \Rightarrow T = \left\{ { - 18; - 17;...;3;4} \right\}\).
Vậy \(S = \left( { - 18} \right) + \left( { - 17} \right) + ... + \left( { - 1} \right) + 0 + 1 + 2 + 3 + 4\)
\(S = - \frac{{18.19}}{2} + \frac{{4.5}}{2} = - 161\).
Chọn B.
Câu hỏi 18 :
Tìm tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \dfrac{1}{3}{x^3} - {x^2} - 3x + m\) có hai điểm cực trị cách đều đường thẳng \(x + 3y + 1 = 0\).
- A \(m = 3\)
- B \(m = \pm 3\)
- C \(m = - 3\)
- D Không có \(m\)
Đáp án: A
Phương pháp giải:
- Tìm điều kiện để đồ thị hàm số có hai điểm cực trị \(A,B\).
- Trung điểm \(I\) của đoạn \(AB\) thuộc đường thẳng \(x + 3y + 1 = 0\)
Lời giải chi tiết:
Ta có: \(y' = {x^2} - 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \Rightarrow y = \dfrac{5}{3} + m\\x = 3 \Rightarrow y = - 9 + m\end{array} \right.\)
Tọa độ hai điểm cực trị là \(A\left( { - 1;\dfrac{5}{3} + m} \right),B\left( {3; - 9 + m} \right)\)
Trung điểm của đoạn\(AB\) là \(I\left( {1; - \dfrac{{11}}{3} + m} \right)\)
Từ yêu cầu đề bài suy ra \(I \in d:x + 3y + 1 = 0\)
\( \Leftrightarrow 1 - 11 + 3m + 1 = 0 \Leftrightarrow m = 3\)
Chọn A.
Câu hỏi 19 :
Tìm số các giá trị nguyên của tham số \(m \in \left( { - 20;\,\,20} \right)\) để hàm số \(y = \left| {{x^4} - 2{x^2} + m} \right|\) có \(7\) điểm cực trị.
- A \(20\)
- B \(18\)
- C \(1\)
- D \(0\)
Đáp án: D
Phương pháp giải:
Số điểm cực trị của hàm số \(y = \left| {f\left( x \right)} \right|\) có \(7\) cực trị \( \Leftrightarrow \) hàm số \(y = f\left( x \right)\) có \(3\) điểm cực trị và đồ thị hàm số \(y = f\left( x \right)\) cắt trục \(Ox\) tại \(4\) điểm phân biệt.
Lời giải chi tiết:
Số điểm cực trị của hàm số \(y = \left| {f\left( x \right)} \right|\) có \(7\) cực trị \( \Leftrightarrow \) hàm số \(y = f\left( x \right)\) có \(3\) điểm cực trị và đồ thị hàm số \(y = f\left( x \right)\) cắt trục \(Ox\) tại \(4\) điểm phân biệt.
Xét hàm số \(y = {x^4} - 2{x^2} + m\) trên \(\mathbb{R}\) ta có: \(y' = 4{x^3} - 4x\)
\( \Rightarrow y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = m\\x = - 1 \Rightarrow y = m - 1\\x = 1 \Rightarrow y = m - 1\end{array} \right.\)
\( \Rightarrow \) Hàm số \(y = {x^4} - 2{x^2} + m\) có \(3\) điểm cực trị với mọi \(m.\)
Ta có \(a > 0 \Rightarrow \) hàm số đã cho có hai điểm cực tiểu và một điểm cực đại.
\( \Rightarrow \) Hàm số có hai điểm cực tiểu là \(\left( { - 1;\,\,m - 1} \right)\) và \(\left( {1;\,\,m - 1} \right),\) điểm cực đại của hàm số là \(\left( {0;\,\,m} \right).\)
\( \Rightarrow \) Đồ thị hàm số \(y = {x^4} - 2{x^2} + m\) cắt trục hoành tại \(4\) điểm phân biệt
\( \Leftrightarrow {y_{CD}}.{y_{CT}} < 0 \Leftrightarrow m\left( {m - 1} \right) < 0 \Leftrightarrow 0 < m < 1.\)
Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \emptyset .\)
Chọn D.
Câu hỏi 20 :
Tìm số các giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( { - 2019;2020} \right)\) để điểm cực tiểu của đồ thị hàm số \(y = {x^3} + {x^2} + mx - 1\) nằm bên phải trục tung.
- A 2020
- B 2019
- C 2017
- D 2018
Đáp án: D
Phương pháp giải:
- Tìm điều kiện để phương trình \(y' = 0\) có ít nhất 1 nghiệm dương.
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2} + 2x + m\).
Để hàm số có cực tiểu thì phương trình \(y' = 0 \Leftrightarrow 3{x^2} + 2x + m = 0\) có hai nghiệm phân biệt.
\( \Rightarrow \Delta ' > 0 \Leftrightarrow 1 - 3m > 0 \Leftrightarrow m < \dfrac{1}{3}\).
Do hệ số \(a = 1 > 0\) nên đồ thị hàm số có điểm cực tiểu nằm bên phải trục tung khi và chỉ khi phương trình \(y' = 0\) có hai nghiệm dương phân biệt hoặc có hai nghiệm trái dấu.
TH1: Phương trình \(y' = 0\) có hai nghiệm dương phân biệt \( \Rightarrow \left\{ \begin{array}{l}S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{ - 2}}{3} > 0\\m > 0\end{array} \right.\) (Vô nghiệm).
TH2: Phương trình \(y' = 0\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0 \Leftrightarrow m < 0\).
Kết hợp điều kiện \( \Rightarrow \left\{ \begin{array}{l}m \in \left( { - 2019;0} \right)\\m \in \mathbb{Z}\end{array} \right. \Rightarrow m \in \left\{ { - 2018; - 2017;...; - 1} \right\}\).
Vậy có 2018 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Chọn D.
Câu hỏi 21 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Hàm số \(y = f\left( {{x^2} - 2x} \right)\) có bao nhiêu điểm cực trị?
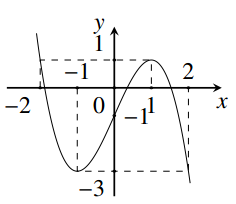
- A \(5\)
- B \(2\)
- C \(3\)
- D \(4\)
Đáp án: C
Phương pháp giải:
- Đặt \(y = g\left( x \right) = f\left( {{x^2} - 2x} \right)\), tính đạo hàm của hàm số.
- Số cực trị của hàm số là số nghiệm bội lẻ của phương trình \(y' = 0.\)
Lời giải chi tiết:
Đặt \(y = g\left( x \right) = f\left( {{x^2} - 2x} \right)\)\( \Rightarrow g'\left( x \right) = \left( {2x - 2} \right)f'\left( {{x^2} - 2x} \right).\)
\(\begin{array}{l}y' = 0 \Leftrightarrow \left( {2x - 2} \right)f'\left( {{x^2} - 2x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x - 2 = 0\\{x^2} - 2x = - 1\\{x^2} - 2x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\end{array}\)
Trong đó \(x = 1\) là nghiệm bội 3, hai nghiệm còn lại là nghiệm đơn.
Vậy hàm số đã cho có 3 điểm cực trị.
Chọn C.
Câu hỏi 22 :
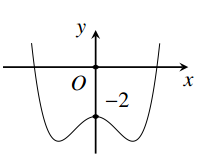
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Hàm số \(y = \left| {f\left( x \right)} \right|\) có bao nhiêu cực trị?
- A \(5\)
- B \(6\)
- C \(3\)
- D \(4\)
Đáp án: A
Phương pháp giải:
- Vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\):
+ Bước 1: Vẽ đồ thị hàm số \(y = f\left( x \right)\).
+ Bước 2: Lấy đối xứng phần đồ thị hàm số \(y = f\left( x \right)\) nằm phía dưới trục \(Ox\) qua trục \(Ox\).
+ Bước 3: Xóa đi phần đồ thị hàm số \(y = f\left( x \right)\) nằm phía dưới trục \(Ox\).
- Dựa vào đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) vừa vẽ, xác định số điểm cực trị (Là điểm mà qua đó đồ thị hàm số chuyển hướng).
Lời giải chi tiết:
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) đề bài cho ta vẽ được đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như sau:
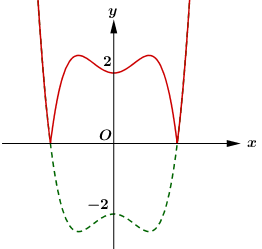
Dựa vào đồ thị ta thấy hàm số \(y = \left| {f\left( x \right)} \right|\) có 5 điểm cực trị.
Chọn A.
Câu hỏi 23 :
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2018;2019} \right]\) để hàm số \(y = m{x^4} + \left( {m + 1} \right){x^2} + 1\) có đúng một điểm cực đại?
- A \(1\)
- B \(2018\)
- C \(2019\)
- D \(0\)
Đáp án: B
Lời giải chi tiết:
Ta có: \(y' = 4m{x^3} + 2\left( {m + 1} \right)x = x\left[ {4m{x^2} + 2\left( {m + 1} \right)} \right]\).
+) TH1: \(m = 0 \Rightarrow y = {x^2} + 1\) \( \Rightarrow \)Loại do hàm số không có cực đại (Đồ thị hàm số là parabol có bề lõm hướng lên).
+) TH2: \(m \ne 0\).
Để hàm số \(y = m{x^4} + \left( {m + 1} \right){x^2} + 1\) có đúng một điểm cực đại thì:
Hoặc: \(\left\{ \begin{array}{l}m < 0\\ - \dfrac{{2\left( {m + 1} \right)}}{{4m}} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\m + 1 \le 0\end{array} \right. \Leftrightarrow m \le - 1\).
Mà \(m \in \mathbb{Z},m \in \left[ { - 2018;2019} \right] \Rightarrow m \in \left\{ { - 2018; - 2017;...; - 1} \right\}:\) 2018 giá trị.
Hoặc: \(\left\{ \begin{array}{l}m > 0\\ - \dfrac{{2\left( {m + 1} \right)}}{{4m}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m + 1 < 0\end{array} \right. \Leftrightarrow m \in \emptyset \)
Vậy có 2018 giá trị của m thỏa mãn.
Chọn: B.
Câu hỏi 24 :
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có bảng xét dấu của \(f'\left( x \right)\) như sau :

Hỏi hàm số \(y = g\left( x \right) = f\left( {{x^2} - 2x - 4} \right)\) có bao nhiêu điểm cực tiểu ?
- A \(3\).
- B \(4\).
- C \(2\).
- D \(1\).
Đáp án: A
Phương pháp giải:
- Lập bảng xét dấu \(g'\left( x \right)\).
- Xác định điểm mà tại đó \(g'\left( x \right)\) đổi dấu từ âm sang dương.
Lời giải chi tiết:
Ta có : \(g'\left( x \right) = 2\left( {x - 1} \right).f'\left( {{x^2} - 2x - 4} \right).\)
\(\begin{array}{l}g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\f'\left( {{x^2} - 2x - 4} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x - 4 = - 2\\{x^2} - 2x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x - 2 = 0\\{x^2} - 2x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 1 \pm \sqrt 3 \\x = 1 \pm \sqrt 5 \end{array} \right.\end{array}\)
Bảng xét dấu \(g'\left( x \right)\) :
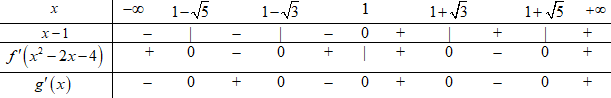
Vậy hàm số \(y = g\left( x \right) = f\left( {{x^2} - 2x - 4} \right)\) có 3 cực tiểu.
Chọn A.
Câu hỏi 25 :
Tìm tất cả các giá trị của m để hàm số \(y = {x^4} - 2m{x^2} + 1\) có 3 cực trị tạo thành một tam giác có diện tích bằng 4
- A \(\sqrt[5]{4}\).
- B \(\sqrt[5]{8}\).
- C \(\sqrt[5]{2}\).
- D \(\sqrt[5]{{16}}\).
Đáp án: D
Phương pháp giải:
- Lấy đạo hàm của hàm số rồi tìm các điểm cực trị \(A,\,\,B,\,\,C\) của đồ thị hàm số.
- Nhận xét: Ba điểm cực trị của hàm trùng phương luôn tạo thành tam giác cân (giả sử cân tại \(A\))
- Gọi \(H\) là trung điểm của \(BC\), chứng minh \(AH \bot BC\).
- Tính \(AH,\,\,BC\), sử dụng công thức tính độ dài đoạn thẳng \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).
- Sử dụng công thức tính diện tích tam giác \({S_{\Delta ABC}} = \dfrac{1}{2}AH.BC\).
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
Ta có \(y' = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right)\).
Cho \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = m\,\,\,\left( 1 \right)\end{array} \right.\)
Để hàm số đã cho có 3 điểm cực trị thì phương trình \(y' = 0\) phải có 3 nghiệm phân biệt, khi đó phương trình (1) phải có 2 nghiệm phân biệt khác \(0\) \( \Rightarrow m > 0\).
Khi đó ta có \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 1\\x = \sqrt m \Rightarrow y = - {m^2} + 1\\x = - \sqrt m \Rightarrow y = - {m^2} + 1\end{array} \right.\).
Suy ra đồ thị hàm số đã cho có 3 điểm cực trị là \(A\left( {0;1} \right)\); \(B\left( {\sqrt m ;1 - {m^2}} \right)\); \(C\left( { - \sqrt m ;1 - {m^2}} \right).\)
Dễ thấy \(A \in Oy\), \(B\) và \(C\) đối xứng nhau qua \(Oy\), do đó tam giác \(ABC\) cân tại \(A\).
Gọi \(H\) là trung điểm của \(BC\)\( \Rightarrow H\left( {0;1 - {m^2}} \right)\) và \(AH \bot BC\) (tính chất tam giác cân).
Ta tính được: \(AH = \sqrt {{{\left( {0 - 0} \right)}^2} + {{\left( {1 - {m^2} - 1} \right)}^2}} = {m^2}\), \(BC = \sqrt {{{\left( {\sqrt m + \sqrt m } \right)}^2} + {{\left( {1 - {m^2} - 1 + {m^2}} \right)}^2}} = 2\sqrt m \).
Theo bài ra ta có: \({S_{ABC}} = 4\) \( \Leftrightarrow \dfrac{1}{2}AH.BC = 4\) \( \Leftrightarrow AH.BC = 8\).
\( \Leftrightarrow {m^2}.2\sqrt m = 8\)\( \Leftrightarrow {\left( {{m^2}\sqrt m } \right)^2} = {4^2}\)\( \Leftrightarrow {m^5} = 16 \Leftrightarrow m = \sqrt[5]{{16}}\,\,\,\left( {tm} \right).\)
Vậy \(m = \sqrt[5]{{16}}\).
Chọn D.
Câu hỏi 26 :
Giá trị thực của tham số \(m\) để hàm số \(y = {x^3} - 3{x^2} + mx - 1\) có hai cực trị \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 6\) là
- A \(3\)
- B \(1\)
- C \( - 3\)
- D \( - 1\)
Đáp án: C
Phương pháp giải:
- Điều kiện để hàm số có 2 điểm cực trị là phương trình \(y' = 0\) có hai nghiệm phân biệt.
- Áp dụng định lí Vi-ét cho phương trình bậc hai \(a{x^2} + bx + c = 0\) là: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\).
- Sử dụng biến đổi \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\), từ đó giải phương trình tìm \(m\).
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\). Ta có: \(y' = 3{x^2} - 6x + m = 0\,\,\,\left( 1 \right)\)
Để hàm số có 2 điểm cực trị thì phương trình (1) phải có 2 nghiệm phân biệt
\( \Leftrightarrow \Delta = {6^2} - 4.3m = 36 - 12m > 0 \Leftrightarrow m < 3.\)
Khi đó hai điểm cực trị của hàm số là \({x_1},\,\,{x_2}\), chính là hai nghiệm phân biệt của phương trình (1), áp dụng định lí Ta-lét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = \dfrac{m}{3}\end{array} \right.\).
Khi đó ta có: \(x_1^2 + x_2^2 = 6\)
\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 6\\ \Leftrightarrow {2^2} - 2.\dfrac{m}{3} = 6\\ \Leftrightarrow m = - 3.\end{array}\)
Chọn C.
Câu hỏi 27 :
Gọi \({m_1},{m_2}\) là các giá trị của tham số m sao cho đồ thị hàm số \(y = {x^3} - 3{x^2} + {m^2} - m + 1\) có hai điểm cực trị là A, B thỏa mãn \({S_{\Delta ABC}} = 7\) với \(C\left( { - 2;4} \right)\). Tổng \(m_1^2 + m_2^2\) bằng
- A \(5\)
- B \(10\)
- C \(13\)
- D \(3\)
Đáp án: C
Lời giải chi tiết:
\(\begin{array}{l}y = {x^3} - 3{x^2} + {m^2} - m + 1\\y' = 3{x^2} - 6x = 0 \Rightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = {m^2} - m + 1\\x = 2 \Rightarrow y = {m^2} - m - 3\end{array} \right.\end{array}\)
\( \Rightarrow \) Hai điểm cực trị của đồ thị hàm số là \(A\left( {0;{m^2} - m + 1} \right)\), \(B\left( {2;{m^2} - m - 3} \right)\).
Thực hiện phép chia đa thức, ta được: \(y = y'.\left( {\dfrac{1}{3}x - \dfrac{1}{3}} \right) - 2x + {m^2} - m + 1\).
Do đó, đường thẳng đi qua 2 điểm cực tiểu và cực đại là \(\left( d \right):y = - 2x + {m^2} - m + 1\) \( \Leftrightarrow - 2x - y + {m^2} - m + 1 = 0\)
\(\begin{array}{l}d\left( {C;d} \right) = \dfrac{{\left| {-2.\left( { - 2} \right) - 4 + {m^2} - m + 1} \right|}}{{\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{{\left| {{m^2} - m + 1} \right|}}{{\sqrt 5 }}\\AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} = \sqrt {{2^2} + {{\left( { - 4} \right)}^2}} = 2\sqrt 5 \\ \Rightarrow {S_{ABC}} = \dfrac{1}{2}.2\sqrt 5 .\dfrac{{\left| {{m^2} - m + 1} \right|}}{{\sqrt 5 }} = 7\\ \Rightarrow \left| {{m^2} - m + 1} \right| = 7\\ \Rightarrow {m^2} - m + 1 = 7\,\,\,\left( {Do\,\,{m^2} - m + 1 > 0\,\,\forall m} \right)\\ \Rightarrow \left[ \begin{array}{l}{m_1} = 3\\{m_2} = - 2\end{array} \right.\\ \Rightarrow m_1^2 + m_2^2 = {3^2} + {\left( { - 2} \right)^2} = 13.\end{array}\)
Chọn C.
Câu hỏi 28 :
Cho hàm số \(y = f\left( x \right)\) có bản biến thiên như sau :
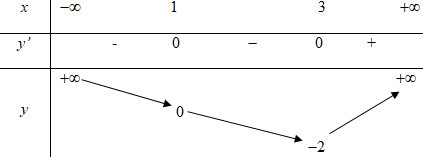
Hàm số \(g\left( x \right) = f\left( {{x^2} - 2x} \right)\) có bao nhiêu điểm cực trị?
- A \(5\)
- B \(3\)
- C \(2\)
- D \(4\)
Đáp án: B
Phương pháp giải:
- Tính \(g'\left( x \right)\), giải phương trình \(g'\left( x \right) = 0\).
- Xác định các nghiệm của phương trình \(g'\left( x \right) = 0\) mà qua đó \(g'\left( x \right)\) đổi dấu.
Lời giải chi tiết:
Ta có: \(g'\left( x \right) = \left( {2x - 2} \right)f'\left( {{x^2} - 2x} \right)\)
\(\begin{array}{l}g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\f'\left( {{x^2} - 2x} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\\x = 3\end{array} \right.\end{array}\)
Ta không xét \({x^2} - 2x = 1\) do qua đó \(f'\left( x \right)\).
Vậy hàm số đã cho có 3 điểm cực trị.
Chọn B.
Câu hỏi 29 :
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên.
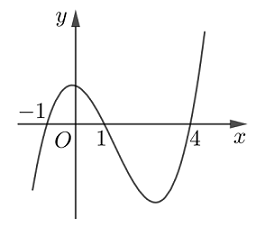
Hàm số \(y = f\left( {{x^2} - 1} \right)\) có bao nhiêu điểm cực trị?
- A \(5\).
- B \(7\).
- C \(4\).
- D \(3\).
Đáp án: A
Phương pháp giải:
- Đặt \(y = g\left( x \right) = f\left( {{x^2} - 1} \right)\).
- Tính đạo hàm hàm số \(y = g\left( x \right)\) (đạo hàm hàm hợp).
- Giải phương trình \(g'\left( x \right) = 0\).
- Lập BBT và kết luận số điểm cực trị của hàm số.
Lời giải chi tiết:
Đặt \(y = g\left( x \right) = f\left( {{x^2} - 1} \right)\).
Ta có : \(g'\left( x \right) = \left( {{x^2} - 1} \right)'.f'\left( {{x^2} - 1} \right) = 2x.f'\left( {{x^2} - 1} \right)\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 1} \right) = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 1 = - 1\\{x^2} - 1 = 1\\{x^2} - 1 = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \\x = \pm \sqrt 5 \end{array} \right.\)
(Tất cả các nghiệm trên đều là nghiệm bội lẻ).
Bảng xét dấu \(g'\left( x \right)\):
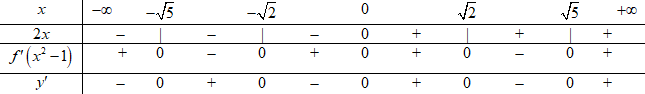
Vậy, hàm số \(y = f\left( {{x^2} - 1} \right)\) có tất cả 5 cực trị.
Chọn A.
Câu hỏi 30 :
Số điểm cực trị của hàm số \(y = {\left| x \right|^3} - 4{x^2} + 3\)là
- A \(4\)
- B \(2\)
- C \(3\)
- D \(0\)
Đáp án: C
Lời giải chi tiết:
TXĐ : ..
Xét hàm số \(y = f\left( x \right) = {x^3} - 4{x^2} + 3\) có :
\(f'\left( x \right) = 3{x^2} - 8x = x\left( {3x - 8} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{8}{3}\end{array} \right.\)
Vẽ đồ thị hàm số \(y = f\left( x \right) = {x^3} - 4{x^2} + 3\) sau đó bỏ đi phần đồ thị bên trái trục tung và lấy đối xứng phần đồ thị bên phải trục tung qua trục tung thì ta được đồ thị hàm số \(y = g\left( x \right) = f\left( {\left| x \right|} \right) = {\left| x \right|^3} - 4{x^2} + 3\) như hình vẽ dưới đây:
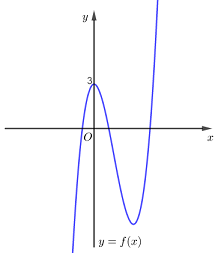
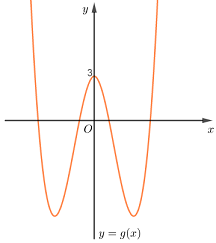
Từ đồ thị hàm số \(y = g\left( x \right)\) ta thấy hàm số \(y = {\left| x \right|^3} - 4{x^2} + 3\) có 3 điểm cực trị.
Chọn C.
Câu hỏi 31 :
Tìm \(m\) để đồ thị hàm số \(y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx + {m^3}\) có hai điểm cực trị \(A,\,B\) sao cho \(AB = \sqrt 2 .\)
- A \(m = 2.\)
- B \(m = 0.\)
- C \(m = 1.\)
- D \(m = 0\) hoặc \(m = 2.\)
Đáp án: A
Phương pháp giải:
Giải phương trình \(y' = 0\) tìm tọa độ hai điểm \(A,B\)
Từ đó sử dụng \(AB = \sqrt 2 \) để tìm \(m.\)
Lời giải chi tiết:
Ta có \(y' = 6{x^2} - 6\left( {m + 1} \right)x + 6m = 0\) \( \Leftrightarrow {x^2} - \left( {m + 1} \right)x + m = 0\)
Có \(\Delta = {\left( {m + 1} \right)^2} - 4m = {\left( {m - 1} \right)^2}\)
Để hàm số có hai cực trị thì \(\Delta > 0 \Leftrightarrow \) \({\left( {m - 1} \right)^2} > 0 \Leftrightarrow m \ne 1\)
Hoành độ hai điểm cực trị: \(\left\{ \begin{array}{l}{x_1} = \dfrac{{m + 1 + m - 1}}{2} = m \Rightarrow y = 3{m^2}\\{x_2} = \dfrac{{m + 1 - m + 1}}{2} = 1 \Rightarrow y = {m^3} + 3m - 1\end{array} \right.\)
Từ đó ta có: \(A\left( {m;3{m^2}} \right),B\left( {1;{m^3} + 3m - 1} \right)\)
\(AB = \sqrt 2 \Leftrightarrow A{B^2} = 2\)
\(\begin{array}{l} \Leftrightarrow {\left( {m - 1} \right)^2} + {\left( {{m^3} - 3{m^2} + 3m - 1} \right)^2} = 2\\ \Leftrightarrow {\left( {m - 1} \right)^2} + {\left( {m - 1} \right)^6} = 2\end{array}\)
Đặt \({\left( {m - 1} \right)^2} = t \ge 0 \Rightarrow {t^3} + t - 2 = 0 \Leftrightarrow t = 1 \Rightarrow m - 1 = 1 \Rightarrow m = 2\)
Chọn A.
Câu hỏi 32 :
Biết \(M\left( {1; - 6} \right)\) là điểm cực tiểu của đồ thị hàm số \(y = 2{x^3} + b{x^2} + cx + 1\). Tìm tọa độ điểm cực đại của đồ thị hàm số đó.
- A \(N\left( {2;6} \right)\)
- B \(N\left( { - 2;11} \right)\)
- C \(N\left( {2;21} \right)\)
- D \(N\left( { - 2;21} \right)\)
Đáp án: D
Phương pháp giải:
\(M\left( {a;b} \right)\) là điểm cực tiểu của hàm số \(y = f\left( x \right)\) thì \(\left\{ \begin{array}{l}f'\left( a \right) = 0\\f\left( a \right) = b\end{array} \right.\) và \(f'\left( x \right)\) đổi dấu từ âm\(\left( - \right)\)sang dương\(\left( + \right)\) khi đi qua điểm \(x = a\).
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
Ta có:\(f'\left( x \right) = 6{x^2} + 2bx + c\)
\(M\left( {1; - 6} \right)\) là điểm cực tiểu của hàm số đã cho nên ta có:
\(\left\{ \begin{array}{l}f'\left( 1 \right) = 0\\f\left( 1 \right) = - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6 + 2b + c = 0\\2 + b + c + 1 = - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2b + c = - 6\\b + c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\c = - 12\end{array} \right.\)
Suy ra
\(\begin{array}{l}f'\left( x \right) = 6{x^2} + 6x - 12 = 6\left( {x - 1} \right)\left( {x + 2} \right)\\ \Rightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\\x = - 2 \Rightarrow f\left( { - 2} \right) = 21\end{array}\)
Do đó \(N\left( { - 2;21} \right)\) là điểm cực đại của đồ thị hàm số đã cho.
Chọn D.
Câu hỏi 33 :
Tìm \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - m + 1} \right)x + 1\) đạt giá trị cực đại tại \(x = 1\).
- A \(m = - 1\).
- B \(m = - 2\).
- C \(m = 2\).
- D \(m = 1\).
Đáp án: C
Phương pháp giải:
Hàm số đạt cực đại tại \(x = a \Leftrightarrow \left\{ \begin{array}{l}y'\left( a \right) = 0\\y''\left( a \right) < 0\end{array} \right.\).
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}y' = {x^2} - 2mx + {m^2} - m + 1\\y'' = 2x - 2m\end{array} \right.\)
Để hàm số đạt cực đại tại \(x = 1\) thì \(\left\{ \begin{array}{l}y'\left( 1 \right) = 0\\y''\left( 1 \right) < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 2 = 0\\2 - 2m < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\\m > 1\end{array} \right. \Leftrightarrow m = 2.\)
Chọn C.
Câu hỏi 34 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số như hình.
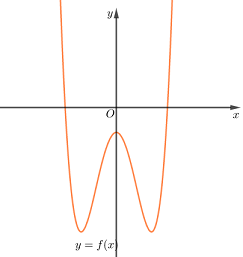
Hàm số \(y = \left| {f\left( {x + 2018} \right)} \right|\) có bao nhiêu điểm cực trị?
- A \(5\)
- B \(2\)
- C \(1\)
- D \(3\)
Đáp án: A
Phương pháp giải:
Dùng phép suy đồ thị, từ đồ thị hàm số \(y = f\left( x \right)\), vẽ đồ thị hàm số \(g\left( x \right) = f\left( {x + 2018} \right)\) bằng cách dịch chuyển đồ thị \(y = f\left( x \right)\) sang bên trái 2018 đơn vị.
Vẽ đồ thị hàm số \(h\left( x \right) = \left| {g\left( x \right)} \right|\) bằng cách lấy đối xứng phần đồ thị \(g\left( x \right)\) phía dưới trục hoành qua trục hoành rồi bỏ đi phần đồ thị phía dưới trục hoành đó.
Từ đồ thị hàm số \(y = h\left( x \right)\) suy ra số điểm cực trị của hàm \(y = h\left( x \right) = \left| {f\left( {x + 2018} \right)} \right|\)
Lời giải chi tiết:
Từ đồ thị hàm số đã cho, ta vẽ được các hàm số sau:
Vẽ đồ thị hàm số \(g\left( x \right) = f\left( {x + 2018} \right)\) bằng cách dịch chuyển đồ thị \(y = f\left( x \right)\) sang bên trái 2018 đơn vị.
Lấy đối xứng phần đồ thị \(g\left( x \right)\) phía dưới trục hoành qua trục hoành rồi bỏ đi phần đồ thị phía dưới trục hoành đó ta được đồ thị của hàm số \(y = h\left( x \right) = \left| {g\left( x \right)} \right| = \left| {f\left( {x + 2018} \right)} \right|\) như hình vẽ dưới đây
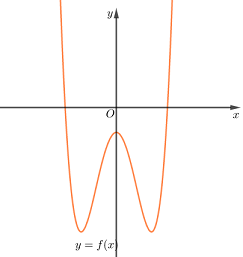
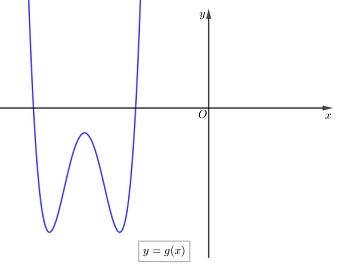
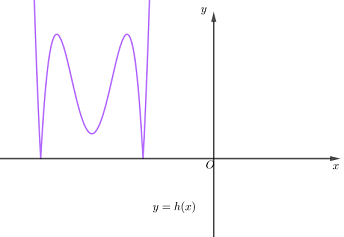
Từ đồ thị hàm số \(y = h\left( x \right)\) ta thấy đồ thị hàm số \(y = \left| {f\left( {x + 218} \right)} \right|\) có 5 điểm cực trị
Chọn A.
Câu hỏi 35 :
Đồ thị của hàm số \(y = - {x^3} + 3{x^2} + 5\) có hai điểm cực trị \(A\) và \(B\). Tính diện tích \(S\) của tam giác \(OAB\) với \(O\) là gốc tọa độ.
- A \(S = \frac{{10}}{3}\)
- B \(S = 9\)
- C \(S = 5\)
- D \(S = 10\)
Đáp án: C
Phương pháp giải:
- Xác định tọa độ các điểm \(A,\,\,B\).
- Viết phương trình đường thẳng \(d\) đi qua hai điểm \(A,\,\,B\).
- Sử dụng công thức tính diện tích \({S_{\Delta OAB}} = \frac{1}{2}d\left( {O;d} \right).AB\).
Lời giải chi tiết:
TXĐ \(D = \mathbb{R}\).
Ta có: \(y' = - 3{x^2} + 6x = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 5\\x = 2 \Rightarrow y = 9\end{array} \right.\).
\( \Rightarrow A\left( {0;5} \right);\,\,B\left( {2;9} \right)\).
Phương trình đường thẳng đi qua \(A\) và \(B\) là: \(\frac{{x - 0}}{{2 - 0}} = \frac{{y - 5}}{{9 - 5}} \Leftrightarrow 2x - y + 5 = 0\,\,\left( d \right)\).
Ta có: \(d\left( {O;d} \right) = \frac{{\left| 5 \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^3}} }} = \sqrt 5 \) , \(AB = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \).
Vậy \({S_{\Delta OAB}} = \frac{1}{2}d\left( {O;d} \right).AB\)\( = \frac{1}{2}\sqrt 5 .2\sqrt 5 = 5\).
Chọn C.
Câu hỏi 36 :
Gọi \(S\) là tập chứa tất cả các giá trị nguyên của \(m\) sao cho hàm số \(y = {x^4} - 2\left( {m - 1} \right){x^2} + {m^2} - m\) có ba điểm cực trị lập thành một tam giác vuông. Tổng tất cả các phần tử của tập \(S\) bằng
- A 2.
- B 1
- C -5.
- D 3.
Đáp án: A
Phương pháp giải:
- Tìm điều kiện để hàm số có 3 điểm cực trị.
- Xác định các điểm cực trị của hàm số.
- Tam giác \(ABC\) vuông tại \(A \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\).
Lời giải chi tiết:
Ta có: \(y' = 4{x^3} - 4\left( {m - 1} \right)x = 4x\left[ {{x^2} - \left( {m - 1} \right)} \right].\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = m - 1\end{array} \right.\)
Để hàm số có 3 điểm cực trị thì phương trình \(y' = 0\) phải có 3 nghiệm phân biệt.
\( \Rightarrow \) Phương trình \({x^2} = m - 1\) có 2 nghiệm phân biệt khác \(0\).
\( \Rightarrow m - 1 > 0 \Leftrightarrow m > 1\).
Khi đó ta có \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = {m^2} - m\\x = \sqrt {m - 1} \Rightarrow y = m - 1\\x = - \sqrt {m - 1} \Rightarrow y = m - 1\end{array} \right.\)
Gọi \(A\left( {0;{m^2} - m} \right);\,\,B\left( {\sqrt {m - 1} ;m - 1} \right);\) \(C\left( { - \sqrt {m - 1} ;m - 1} \right)\).
Tam giác \(ABC\) cân tại \(A\), do đó để \(ABC\) là tam giác vuông thì phải vuông tại \(A\).
Ta có: \(\overrightarrow {AB} = \left( {\sqrt {m - 1} ; - {m^2} + 2m - 1} \right);\,\,\)\(\overrightarrow {AC} = \left( { - \sqrt {m - 1} ; - {m^2} + 2m - 1} \right)\).
\(\Delta ABC\) vuông tại \(A \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\).
\(\begin{array}{l} \Leftrightarrow - \left( {m - 1} \right) + {\left( {m - 1} \right)^4} = 0\\ \Leftrightarrow \left( {m - 1} \right)\left[ {{{\left( {m - 1} \right)}^3} - 1} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m - 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\,\,\left( {ktm} \right)\\m = 2\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(S = \left\{ 2 \right\}\) nên tổng các phần tử của \(S\) bằng 2.
Chọn A.
Câu hỏi 37 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) liên tục trên R và đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ.
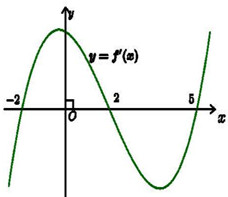
Gọi \(S\) là tập hợp tất cả các giá trị nguyên của \(m\) để hàm số \(y = f\left( {\left| {x + 1} \right| - m} \right)\) có 3 điểm cực trị. Tổng tất cả các phần tử của tập hợp \(S\) bằng ?
- A \( - 12\)
- B \( - 9\)
- C \( - 7\)
- D \( - 14\)
Đáp án: B
Phương pháp giải:
Hàm số \(y = f\left( {\left| x \right|} \right)\) có \(2a + 1\) điểm cực trị khi hàm số \(y = f\left( x \right)\) có \(a\) điểm cực trị dương.
Lời giải chi tiết:
Hàm số \(y = f\left( x \right)\) có 3 điểm cực trị là \( - 2,\,\,2,\,\,5\).
Nên hàm số \(y = f\left( {\left( {x + 1} \right) - m} \right)\) có 3 điểm cực trị là \(\left[ \begin{array}{l}x + 1 - m = - 2\\x + 1 - m = 2\\x + 1 - m = 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = m - 3\\x = m + 1\\x = m + 4\end{array} \right.\)
Hàm số \(y = f\left( {\left( {x + 1} \right) - m} \right)\) có đúng 3 điểm cực trị khi \(y = f\left( {\left( {x + 1} \right) - m} \right)\) có đúng 1 cực trị lớn hơn \( - 1\).
Do đó \(\left\{ \begin{array}{l}m - 3 \le - 1\\m + 1 \le - 1\\m + 4 > - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 2\\m \le - 2\\m > - 5\end{array} \right. \Leftrightarrow - 5 < m \le - 2\). Mà \(m \in \mathbb{Z}\) \( \Rightarrow m \in \left\{ { - 4; - 3; - 2} \right\}\)
Vậy \(S = - 4 - 3 - 2 = - 9\).
Chọn B.
Câu hỏi 38 :
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + {m^2}} \right|\) có đúng 5 điểm cực trị?
- A \(6\).
- B \(4\).
- C \(5\).
- D \(7\).
Đáp án: D
Phương pháp giải:
Đánh giá số điểm cực trị của hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + {m^2}} \right|\) dựa vào hàm số \(y = 3{x^4} - 4{x^3} - 12{x^2}\).
Lời giải chi tiết:
Xét hàm số \(f\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2}\) có \(f'\left( x \right) = 12{x^3} - 12{x^2} - 24x = 12x\left( {{x^2} - x - 2} \right),\)\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\end{array} \right.\)
Bảng biến thiên:
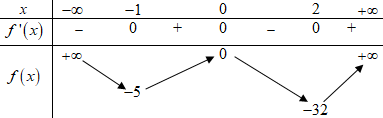
Nhận xét: Hàm số \(f\left( x \right)\) có 3 cực trị là \(x = - 1,x = 0,x = 2\). Để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + {m^2}} \right| = \left| {f\left( x \right) + {m^2}} \right|\) có đúng 5 cực trị thì đường thẳng \(y = - {m^2}\) hoặc cắt đồ thị hàm số \(y = f\left( x \right)\) tại 2 điểm phân biệt, khác các điểm cực trị hoặc cắt đồ thị hàm số tại 3 điểm phân biệt, trong đó có 1 điểm cực trị.
\( \Leftrightarrow \left[ \begin{array}{l} - {m^2} \ge 0\\ - 32 \le - {m^2} \le - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\\sqrt 5 \le \left| m \right| \le \sqrt {32} \end{array} \right.\)
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;3;4;5; - 3; - 4; - 5} \right\}\): có 7 giá trị thỏa mãn.
Chọn: D.
Câu hỏi 39 :
Tìm tất cả các giá trị của m để hàm số \(y = {\left| x \right|^3} + m{x^2} + 3\left| x \right| + 1\) có 5 điểm cực trị
- A \(m > - 3\).
- B \(m < - 3\).
- C \(m \le - 3\).
- D \(m \ge - 3\).
Đáp án: B
Phương pháp giải:
Hàm số \(y = f\left( {\left| x \right|} \right)\) có 5 cực trị khi và chỉ khi hàm số \(y = f\left( x \right)\) có 2 cực trị cùng dấu dương.
Lời giải chi tiết:
Đặt \(f\left( x \right) = {x^3} + m{x^2} + 3x + 1\).
Để hàm số \(y = f\left( {\left| x \right|} \right)\) có 5 cực trị khi và chỉ khi hàm số \(y = f\left( x \right)\) có 2 cực trị cùng dấu dương. Suy ra phương trình \(f'\left( x \right) = 0\) có 2 nghiệm dương phân biệt.
Ta có: \(f'\left( x \right) = 3{x^2} + 2mx + 3 = 0\) có 2 nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\S > 0\\P > 0\end{array} \right.\).
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 9 > 0\\ - \dfrac{{2m}}{3} > 0\\\dfrac{3}{3} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 3\\m < - 3\end{array} \right.\\m < 0\end{array} \right. \Leftrightarrow m < - 3\).
Chọn B.
Câu hỏi 40 :
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \dfrac{{{x^2} + mx + 2m}}{{x + 1}}\) có hai điểm cực trị \(A,\,\,B\) và tam giác \(OAB\) vuông tại O. Tổng tất cả các phần tử của \(S\) là:
- A \(9\).
- B \(1\).
- C \(4\).
- D \(5\).
Đáp án: A
Phương pháp giải:
- Chia tử cho mẫu, tính đạo hàm của hàm số.
- Tìm điều kiện để hàm số có 2 điểm cực trị (phương trình \(y' = 0\) có 2 nghiệm thỏa mãn ĐKXĐ).
- Áp dụng định lí Vi-ét.
- Điều kiện cần và đủ để tam giác \(OAB\) vuông tại \(O\) là \(\overrightarrow {OA} .\overrightarrow {OB} = 0\).
- Giải phương trình tìm \(m\) và đối chiếu điều kiện.
Lời giải chi tiết:
ĐKXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có: \(y = \dfrac{{{x^2} + mx + 2m}}{{x + 1}} = x + m - 1 + \dfrac{{m + 1}}{{x + 1}}\).
\( \Rightarrow y' = 1 - \dfrac{{m + 1}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{{{x^2} + 2x - m}}{{{{\left( {x + 1} \right)}^2}}}\)
Để hàm số đã cho có 2 cực trị thì phương trình \(y' = 0\) phải có 2 nghiệm phân biệt khác \( - 1\).
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = 1 + m > 0\\1 - 2 - m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - 1\\m \ne - 1\end{array} \right. \Leftrightarrow m > - 1.\)
Khi đó, giả sử \({x_1},\,\,{x_2}\) là nghiệm phân biệt của phương trình \(y' = 0\), áp dụng định lí Vi-ét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}.{x_2} = - m\end{array} \right..\)
Đặt \(A\left( {{x_1};{x_1} + m - 1 + \dfrac{{m + 1}}{{{x_1} + 1}}} \right),\,\,B\left( {{x_2};{x_2} + m - 1 + \dfrac{{m + 1}}{{{x_2} + 1}}} \right)\) là hai điểm cực trị của hàm số.
Để tam giác \(OAB\) vuông tại \(O\) thì \(\overrightarrow {OA} .\overrightarrow {OB} = 0\).
\(\begin{array}{l} \Leftrightarrow {x_1}.{x_2} + \left( {{x_1} + m - 1 + \dfrac{{m + 1}}{{{x_1} + 1}}} \right)\left( {{x_2} + m - 1 + \dfrac{{m + 1}}{{{x_2} + 1}}} \right) = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\left( {\dfrac{{{x_1}}}{{{x_2} + 1}} + \dfrac{{{x_2}}}{{{x_1} + 1}}} \right)\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\left( {\dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}}} \right) + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}} = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\dfrac{{x_1^2 + x_2^2 + {x_1} + {x_2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}}\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\dfrac{{{x_1} + {x_2} + 2}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\dfrac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} + {x_1} + {x_2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}}\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\dfrac{{{x_1} + {x_2} + 2}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} = 0\\ \Leftrightarrow - 2m - 2\left( {m - 1} \right) + \left( {m + 1} \right).\dfrac{{2 + 2m}}{{ - m - 1}} + {\left( {m - 1} \right)^2} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{ - m - 1}} = 0\\ \Leftrightarrow - 2m - 2m + 2 - 2 - 2m + {m^2} - 2m + 1 - m - 1 = 0\\ \Leftrightarrow {m^2} - 9m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 9\end{array} \right.\,\,\left( {tm} \right)\end{array}\)
\( \Rightarrow S = \left\{ {0;9} \right\}\).
Vậy tổng tất cả các phần tử của S là \(9\).
Chọn A.
Tổng hợp bài tập trắc nghiệm cực trị của hàm số mức độ thông hiểu có đáp án và lời giải chi tiết
Tổng hợp bài tập trắc nghiệm cực trị của hàm số mức độ nhận biết có đáp án và lời giải chi tiết
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục