30 bài tập số phức mức độ nhận biết
Làm đề thiCâu hỏi 1 :
Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện \(|z|=5\) và \(z=\bar{z}\).
- A 1
- B 2
- C 3
- D 4
Đáp án: B
Phương pháp giải:
Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\) , thay vào các hệ thức trong bài và tìm \(a,b\).
Lời giải chi tiết:
Giả sử số phức cần tìm là \(z=a+bi\).
Từ điều kiện \(z=\bar{z}\) ta có \(a+bi=a-bi\Leftrightarrow b=0\)
Từ điều kiện \(|z|=5\Rightarrow a=\pm 5\)
Chọn B
Câu hỏi 2 :
Có bao nhiêu số phức thỏa mãn đồng thời các điều kiện \(|z|=4\) và \(z=-\bar{z}\).
- A 1
- B 2
- C 3
- D 4
Đáp án: B
Phương pháp giải:
Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\)
Lời giải chi tiết:
Giả sử số phức cần tìm là \(z=a+bi\).
Từ điều kiện \(z=-\bar{z}\) ta có \(a+bi=-(a-bi)\Leftrightarrow a=0\)
Từ điều kiện \(|z|=4\Rightarrow b=\pm 4\)
Chọn B
Câu hỏi 3 :
Tìm số điểm biểu diễn cho số phức z thỏa mãn đồng thời các điều kiện: \(|z+4|=3|z|\) và z là thuần ảo?
- A 1
- B 0
- C 3
- D 2
Đáp án: D
Phương pháp giải:
Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\).
Điểm biểu diễn số phức \(z=a+bi\) trên mặt phẳng phức có tọa độ \(\left( a;b \right)\).
Lời giải chi tiết:
Vì z là thuần ảo nên \(a=0\Rightarrow z=bi\). Từ điều kiện \(|z+4|=3|z|\) có
\(\left| bi+4 \right|=3\left| bi \right|\Leftrightarrow{{b}^{2}}+{{4}^{2}}=9{{b}^{2}}\Leftrightarrow 8{{b}^{2}}=16\Leftrightarrow {{b}^{2}}=2\Leftrightarrow b=\pm \sqrt{2}\)
Mỗi một số phức z chỉ có 2 điểm biểu diễn trên mặt phẳng phức.
Chọn D
Câu hỏi 4 :
Tìm số điểm biểu diễn cho số phức z thỏa mãn đồng thời các điều kiện: \(|z+2i|=|z+4|\) và phần ảo của z bằng 0?
- A 1
- B 0
- C 3
- D 2
Đáp án: A
Phương pháp giải:
Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\).
Điểm biểu diễn số phức \(z=a+bi\) trên mặt phẳng phức có tọa độ \(\left( a;b \right)\).
Lời giải chi tiết:
Vì phần ảo của z bằng 0 nên giả sử \(z=a\), từ điều kiện \(|z+2i|=|z+4|\) có
\(|a+2i|=|a+4|\Leftrightarrow {{a}^{2}}+4={{(a+4)}^{2}}\Leftrightarrow 8a+12=0\Leftrightarrow a=-\frac{3}{2}\).
Suy ra \(z=-\frac{3}{2}\).
Mỗi một số phức z chỉ có 1 điểm biểu diễn trên mặt phẳng phức.
Chọn A
Câu hỏi 5 :
Số phức z thỏa mãn đồng thời các điều kiện \(|z-5|=|z-2-3i|\) và phần thực, phần ảo của z có giá trị đối nhau là
- A \(z=-2+2i\)
- B \(z=2-2i\)
- C \(z=1-i\)
- D \(z=-1+i\)
Đáp án: C
Phương pháp giải:
Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\Rightarrow z\).
Lời giải chi tiết:
Giả sử số phức cần tìm là \(z=a+bi\).
Vì phần thực, phần ảo của z có giá trị đối nhau nên \(a+b=0\) .(1)
Từ điều kiện \(|z-5|=|z-2-3i|\) có
\(|a+bi-5|=|a+bi-2-3i| \)
\(\Leftrightarrow {{(a-5)}^{2}}+{{b}^{2}}={{(a-2)}^{2}}+{{(b-3)}^{2}}\)
\(\Leftrightarrow -10a+25=-4a+4-6b+9\)
\(\Leftrightarrow -6a+6b=-12\Leftrightarrow -a+b=-2\) (2)
Giải hệ (1) (2) có \(b=-1,a=1\Rightarrow z=1-i\).
Chọn C.
Câu hỏi 6 :
Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện: \(|z+6|=5\) và phần ảo của z bằng 4?
- A 1
- B vô số
- C 4
- D 2
Đáp án: D
Phương pháp giải:
Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\Rightarrow z\).
Lời giải chi tiết:
Vì z có phần ảo bằng 4 nên \(z=a+4i\).
Từ điều kiện \(|z+6|=5\) có
\(\begin{array}{l}
\left| {a + 4i + 6} \right| = 5 \Leftrightarrow {(a + 6)^2} + {4^2} = {5^2}\\
\Leftrightarrow {(a + 6)^2} = 9 \\ \Leftrightarrow a + 6 = \pm 3 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{a = - 3}\\
{a = - 9}
\end{array}} \right.
\end{array}\)
Phương trình có 2 nghiệm. Suy ra tìm được 2 số phức thỏa mãn.
Chọn D
Câu hỏi 7 :
Cho số phức \(z=5-4i.\) Số phức đối của \(z\) có điểm biểu diễn hình học là
- A \(\left( 5;4 \right).\)
- B \(\left( 5;-\,4 \right).\)
- C \(\left( -\,5;-\,4 \right).\)
- D \(\left( -\,5;4 \right).\)
Đáp án: D
Phương pháp giải:
Số phức \(z=a+bi\) có số phức đối là \(z'=-\,a-bi\) và điểm biểu diễn số phức z’ trong mặt phẳng là : \(M\left( -a;\ -b \right).\)
Lời giải chi tiết:
Ta có \(z=5-4i\,\,\Rightarrow \,\,\)Số phức đối của \(z\) là \(w=-\,5+4i\) và có điểm biểu diễn hình học là \(\left( -\,5;4 \right).\)
Chọn D
Câu hỏi 8 :
Tìm số phức z thỏa mãn \(\overline z = 2 - i\) là
- A \(z = 2 + i\).
- B \(z = 1 - 2i\).
- C \(z = - 2 - i\).
- D \(z = - 2 + i\).
Đáp án: A
Phương pháp giải:
Số phức \(z = a + bi\) có số phức liên hợp \(\overline z = a - bi\).
Lời giải chi tiết:
Ta có \(\overline z = 2 - i \Rightarrow z = 2 + i.\)
Chọn A.
Câu hỏi 9 :
Cho số phức \(z = 3 + 2i\). Giá trị của \(z.\overline z \) bằng
- A \(5\)
- B \(9\)
- C \(13\)
- D \(\sqrt {13} \)
Đáp án: C
Phương pháp giải:
Sử dụng công thức \(z.\overline z = {\left| z \right|^2}\).
Lời giải chi tiết:
\(z.\overline z = {\left| z \right|^2} = {3^2} + {2^2} = 13.\)
Chọn C.
Câu hỏi 10 :
Cho hai số phức \({z_1} = - 1 + 2i;\) \({z_2} = 1 + 2i\). Tinh \(T = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}\)
- A \(T = 2\sqrt 5 \)
- B \(T = 4\)
- C \(T = 10\)
- D \(T = 7\)
Đáp án: C
Phương pháp giải:
Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết:
Ta có
\(\begin{array}{l}{z_1} = - 1 + 2i \Rightarrow \left| {{z_1}} \right| = \sqrt {{{\left( { - 1} \right)}^2} + {2^2}} = \sqrt 5 \\{z_2} = 1 + 2i \Rightarrow \left| {{z_2}} \right| = \sqrt {{1^2} + {2^2}} = \sqrt 5 \end{array}\)
Vậy \(T = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 5 + 5 = 10.\)
Chọn C.
Câu hỏi 11 :
Số phức \(z = 8 - 7i\) có phần thực và phần ảo lần lượt bằng
- A 8 và \( - 7i\)
- B 8 và 7.
- C 8 và \(7i\)
- D 8 và \( - 7\)
Đáp án: D
Phương pháp giải:
Số phức \(z = a + bi\) có phần thực là a và phần ảo là b.
Lời giải chi tiết:
Số phức \(z = 8 - 7i\) có phần thực là 8 và phần ảo là \( - 7\).
Chọn D.
Câu hỏi 12 :
Điểm M trong hình bên là điểm biểu diễn hình học của số phức nào dưới đây?
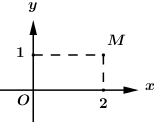
- A \(z = 1 - 2i\)
- B \(z = 2 + i\)
- C \(z = 1 + 2i\)
- D \(z = 2 - i\)
Đáp án: B
Phương pháp giải:
Điểm \(M\left( {a;b} \right)\) là điểm biểu diễn hình học của số phức \(z = a + bi\).
Lời giải chi tiết:
Ta thấy \(M\left( {2;1} \right)\) nên nó biểu diễn cho số phức \(z = 2 + i\).
Chọn B.
Câu hỏi 13 :
Điểm biểu diễn số phức \(z = 1 - 2i\) có tọa độ là:
- A \(\left( { - 1;2} \right)\)
- B \(\left( {1; - 2} \right)\)
- C \(\left( { - 2;1} \right)\)
- D \(\left( {1;2} \right)\)
Đáp án: B
Phương pháp giải:
Điểm biểu diễn số phức \(z = a + bi\) có tọa độ là: \(M\left( {a;b} \right)\).
Lời giải chi tiết:
Điểm biểu diễn số phức \(z = 1 - 2i\) có tọa độ là: \(\left( {1; - 2} \right).\)
Chọn B.
Câu hỏi 14 :
Cho số phức \(z = 2 - 5i.\) Phần thực và phần ảo của số phức liên hợp \(\bar z\) là
- A Phần thực bằng 2, phần ảo bằng \(5.\)
- B Phần thực bằng 2, phần ảo bằng \( - 5i.\)
- C Phần thực bằng 2, phần ảo bằng \(5i.\)
- D Phần thực bằng 2, phần ảo bằng \( - 5.\)
Đáp án: A
Phương pháp giải:
- Số phức \(z = a + bi\) có số phức liên hợp \(\bar z = a - bi\).
- Số phức \(z = a + bi\) có phần thực bằng \(a\), phần ảo bằng \(b\).
Lời giải chi tiết:
\(z = 2 - 5i \Rightarrow \bar z = 2 + 5i\).
Vậy số phức \(\bar z\) có phần thực bằng 2, phần ảo bằng \(5.\)
Chọn A.
Câu hỏi 15 :
Cho số phức \(z = 1 + 2i.\)Tìm môđun của số phức \(\overline z .\)
- A \(\sqrt 5 .\)
- B \( - 1.\)
- C \(\sqrt 3 .\)
- D \(3.\)
Đáp án: A
Phương pháp giải:
Số phức \(z = x + yi\,\,\left( {x,y \in \mathbb{R}} \right)\) có số phức liên hợp \(\overline z = x - yi\) và \(\left| z \right| = \left| {\overline z } \right| = \sqrt {{x^2} + {y^2}} \).
Lời giải chi tiết:
\(z = 1 + 2i \Rightarrow \)\(\left| z \right| = \left| {\overline z } \right| = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \).
Chọn A.
Câu hỏi 16 :
Cho số phức \(z = 4 - 3i.\) Khi đó \(\left| z \right|\) bằng:
- A \(25\)
- B \(5\)
- C \(7\)
- D \(\sqrt 7 \)
Đáp án: B
Phương pháp giải:
Modun của số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\) là: \(\left| z \right| = \sqrt {{x^2} + {y^2}} .\)
Lời giải chi tiết:
Ta có: \(z = 4 - 3i\) \( \Rightarrow \left| z \right| = \sqrt {{4^2} + {{\left( { - 3} \right)}^2}} = 5.\)
Chọn B.
Câu hỏi 17 :
Số phức nào sau đây có biểu diễn hình học là điểm \(M\left( {3; - 5} \right).\)
- A \(z = 3 - 5i\)
- B \(z = - 3 - 5i\)
- C \(z = 3 + 5i\)
- D \(z = - 3 + 5i\)
Đáp án: A
Phương pháp giải:
Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\)
Lời giải chi tiết:
Điểm \(M\left( {3; - 5} \right)\) là điểm biểu diễn hình học của số phức \(z = 3 - 5i.\)
Chọn A.
Câu hỏi 18 :
Modun của số phức \(z = \sqrt 3 - i\) bằng:
- A \(\sqrt 2 \)
- B \(1\)
- C \(4\)
- D \(2\)
Đáp án: D
Phương pháp giải:
Modun của số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\) là: \(\left| z \right| = \sqrt {{x^2} + {y^2}} .\)
Lời giải chi tiết:
Ta có: \(z = \sqrt 3 - 1\) \( \Rightarrow \left| z \right| = \sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { - 1} \right)}^2}} = 2.\)
Chọn D.
Câu hỏi 19 :
Phần ảo của số phức \(z = 3 + 2i\) bằng:
- A \(3\)
- B \(2\)
- C \(2i\)
- D \( - 2\)
Đáp án: B
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) thì \(a\) là phần thực, \(b\) là phần ảo của số phức \(z.\)
Lời giải chi tiết:
Số phức \(z = 3 + 2i\) có phẩn ảo là \(2.\)
Chọn B.
Câu hỏi 20 :
Trên mặt phẳng tọa độ, điểm biểu diễn số phức \(z = 5 + 8i\) là điểm nào dưới đây?
- A \(M\left( { - 5; - 8} \right)\)
- B \(N\left( { - 5;\,\,8} \right)\)
- C \(P\left( {5;\,\,8} \right)\)
- D \(Q\left( {5; - 8} \right)\)
Đáp án: C
Phương pháp giải:
Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\)
Lời giải chi tiết:
Điểm biểu diễn số phức \(z = 5 + 8i\) là: \(P\left( {5;\,\,8} \right).\)
Chọn C.
Câu hỏi 21 :
Số phức liên hợp của \(z = 5 + 4i\) là:
- A \(\overline z = - 5 - 4i\)
- B \(\overline z = 4 - 5i\)
- C \(\overline z = 5 - 4i\)
- D \(\overline z = 4 + 5i\)
Đáp án: C
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\)
Lời giải chi tiết:
Số phức liên hợp của số phức \(z = 5 + 4i\) là: \(\overline z = 5 - 4i.\)
Chọn C.
Câu hỏi 22 :
Cho số phức \(z = 3 - 4i\) Modun của \(z\) bằng
- A \(7\)
- B \(1\)
- C \(12\)
- D \(5\)
Đáp án: D
Phương pháp giải:
Modun của số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\) là: \(\left| z \right| = \sqrt {{x^2} + {y^2}} .\)
Lời giải chi tiết:
Modun của số phức \(z = 3 - 4i\) là: \(\left| z \right| = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5.\)
Chọn D.
Câu hỏi 23 :
Phần ảo của số phức \(z = 4 - 5i\) là:
- A \(4\)
- B \( - 5i\)
- C \( - 5\)
- D \(5\)
Đáp án: C
Phương pháp giải:
Số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có phần thực là \(a\) và phần ảo là \(b.\)
Lời giải chi tiết:
Số phức \(z = 4 - 5i\) có phần thực là \(4\) và phần ảo là \( - 5.\)
Chọn C.
Câu hỏi 24 :
Cho số phức \(z = 2 + 3i.\) Phần ảo của số phức \(\overline z \) là:
- A \( - 3i\)
- B \( - 3\)
- C \( - 2\)
- D \( - 2i\)
Đáp án: B
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\)
Số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có phần thực là \(a,\) phần ảo là \(b.\)
Lời giải chi tiết:
Ta có:\(z = 2 + 3i\) \( \Rightarrow \overline z = 2 - 3i\)
\( \Rightarrow \overline z \) có phần ảo là \( - 3.\)
Chọn B.
Câu hỏi 25 :
Cho số phức \(z = 2 + 3i\) có điểm biểu diễn trên mặt phẳng tọa độ là:
- A \(Q\left( {2; - 3} \right)\)
- B \(N\left( {2;\,\,3} \right)\)
- C \(M\left( { - 2;\,\,3} \right)\)
- D \(P\left( { - 2; - 3} \right)\)
Đáp án: B
Phương pháp giải:
Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\)
Lời giải chi tiết:
Điểm biểu diễn của số phức \(z = 2 + 3i\) là: \(\left( {2;\,\,3} \right).\)
Chọn B.
Câu hỏi 26 :
Số phức liên hợp của số phức \(z = 2 - 5i\) là:
- A \(\overline z = - 2 + 5i\)
- B \(\overline z = 2 - 5i\)
- C \(\overline z = - 2 - 5i\)
- D \(\overline z = 2 + 5i\)
Đáp án: D
Phương pháp giải:
Số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có số phức liên hợp là:\(\overline z = a - bi.\)
Lời giải chi tiết:
Số phức liên hợp của số phức \(z = 2 - 5i\) là: \(\overline z = 2 + 5i.\)
Chọn D.
Câu hỏi 27 :
Số phức \(z = 4 - 3i\) có phần ảo bằng:
- A \( - 3i\)
- B \( - 3\)
- C \(3\)
- D \(4\)
Đáp án: B
Phương pháp giải:
Số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có phần thực là \(a\) và phần ảo là \(b.\)
Lời giải chi tiết:
Ta có: \(z = 4 - 3i\) có phần thực là \(4\) và phần ảo là \( - 3.\)
Chọn B.
Câu hỏi 28 :
Số phức liên hợp của \(z = 3 + 2i\) là:
- A \(\overline z = 2 - 3i\)
- B \(\overline z = 3 - 2i\)
- C \(\overline z = - 2 - 3i\)
- D \(\overline z = - 2 - 2i\)
Đáp án: B
Phương pháp giải:
Cho số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right),\) ta có số phức liên hợp của số phức \(z\) là:\(\overline z = a - bi.\)
Lời giải chi tiết:
Ta có:\(z = 3 + 2i \Rightarrow \overline z = 3 - 2i.\)
Chọn B.
Câu hỏi 29 :
Điểm \(M\left( {3; - 1} \right)\) là điểm biểu diễn của số phức nào sau đây?
- A \(z = 1 - 3i\)
- B \(z = - 3 + i\)
- C \(z = 3 - i\)
- D \(z = - 1 + 3i\)
Đáp án: C
Phương pháp giải:
Điểm \(M\left( {x;\,\,y} \right)\) là điểm biểu diễn số phức \(z = x + yi.\)
Lời giải chi tiết:
Ta có: Điểm \(M\left( {3; - 1} \right)\) là điểm biểu diễn số phức \(z = 3 - i.\)
Chọn C.
Câu hỏi 30 :
Môđun của số phức \(z = - 2 - i\) bằng:
- A \(3\)
- B \(5\)
- C \(\sqrt 3 \)
- D \(\sqrt 5 \)
Đáp án: D
Phương pháp giải:
Áp dụng công thức tính môđun số phức: \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết:
\(z = 2 - i \Rightarrow \left| z \right| = \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} = \sqrt 5 \).
Chọn D.
Tổng hợp các bài tập trắc nghiệm số phức mức độ thông hiểu có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm số phức mức độ vận dụng, vận dụng cao có đáp án và lời giải chi tiết
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục









