 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Đề ôn tập học kì 1 – Có đáp án và lời giải
Đề ôn tập học kì 1 – Có đáp án và lời giải
Đề số 10 - Đề kiểm tra học kì 1 - Toán 7
Đáp án và lời giải chi tiết Đề số 10 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 7
Đề bài
Bài 1 (1,5 điểm):Thực hiện phép tính:
\(a)\,\,\dfrac{3}{2} - \dfrac{3}{2}:\dfrac{{ - 1}}{{{2^3}}}\)
\(b)\,\,23\dfrac{1}{3}:\dfrac{{ - 1}}{{{2^2}}} - 13\dfrac{1}{3}:\dfrac{{ - 1}}{{{2^2}}} + 5\sqrt {\dfrac{9}{{25}}} \)
Bài 2 (1,5 điểm):Cho hàm số \(y = 3x\)
a) Vẽ đồ thị hàm số trên.
b) Điểm \(M( - 2; - 6)\) có thuộc đồ thị hàm số \(y = 3x\) không? Vì sao?
Bài 3 (2,5 điểm):Tìm \(x,\,\,y\) biết:
a) \(\dfrac{1}{3} + \dfrac{2}{3}:x = - 2\)
b)\(7x = 3y\) và \(2x - y = 16\)
c) Một nhân viên văn phòng có thể đánh máy được \(160\) từ trong \(2,5\) phút. Hỏi cần bao nhiêu phút để người đó đánh được \(800\) từ? (giả thiết rằng thời gian để đánh được các từ là như nhau).
Bài 4 (3,5 điểm):Cho tam giác \(ABC\) vuông tại \(A\) có \(\angle B = {60^0}\). Vẽ \(AH \bot BC\) tại \(H\).
a) Tính số đo \(\angle HAB\).
b) Trên cạnh \(AC\) lấy điểm \(D\) sao cho \(AD = AH\). Gọi \(I\) là trung điểm của cạnh \(HD\). Chứng minh \(\Delta AHI = \Delta ADI\). Từ đó suy ra \(AI \bot HD\).
c) Tia \(AI\) cắt cạnh \(HC\) tại điểm \(K\). Chứng minh \(\Delta AHK = \Delta ADK\), từ đó suy ra \(AB\)//\(KD\).
d) Trên tia đối của tia \(HA\) lấy điểm \(E\) sao cho \(HE = AH\). Chứng minh \(H\) là trung điểm của \(BK\) và ba điểm \(D,\,\,K,\,\,E\) thẳng hàng.
Bài 5 (1,0 điểm):
a) Tính: \(\dfrac{1}{{1.3}} + \dfrac{1}{{3.5}} + \dfrac{1}{{5.7}} + ... + \dfrac{1}{{19.21}}\)
b) Chứng minh: \(A = \dfrac{1}{{1.3}} + \dfrac{1}{{3.5}} + \dfrac{1}{{5.7}} \)\(+ ... + \dfrac{1}{{(2n - 1)(2n + 1)}} < \dfrac{1}{2}\).
Lời giải chi tiết
Bài 1:
\(\begin{array}{l}a)\,\,\dfrac{3}{2} - \dfrac{3}{2}:\dfrac{{ - 1}}{{{2^3}}}\,\, \\= \,\,\,\dfrac{3}{2} - \dfrac{3}{2}:\dfrac{{ - 1}}{8}\,\,\\ = \,\,\,\dfrac{3}{2} - \dfrac{3}{2} \cdot \dfrac{8}{{ - 1}}\,\, \\= \,\dfrac{3}{2} - ( - 12) = \dfrac{3}{2} + 12 \\= \dfrac{3}{2} + \dfrac{{24}}{2} = \dfrac{{27}}{2}\,\,\,\,\,\,\,\\b)\,\,23\dfrac{1}{3}:\dfrac{{ - 1}}{{{2^2}}} - 13\dfrac{1}{3}:\dfrac{{ - 1}}{{{2^2}}} + 5\sqrt {\dfrac{9}{{25}}} \\= 23\dfrac{1}{3}:\dfrac{{ - 1}}{4} - 13\dfrac{1}{3}:\dfrac{{ - 1}}{4} + 5.\dfrac{3}{5}\\ = \left( {23\dfrac{1}{3} - 13\dfrac{1}{3}} \right):\dfrac{{ - 1}}{4} + 3 \\= 10:\dfrac{{ - 1}}{4} + 3 = 10.\dfrac{4}{{ - 1}} + 3 \\= - 40 + 3 = - 37\end{array}\)
Bài 2:
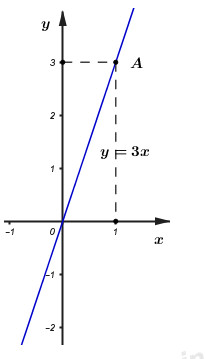
a) Vẽ hệ trục tọa độ \(Oxy\).
Với \(x = 1\) ta được \(y = 3\). Điểm \(A\,\,(1\,;\,\,3)\) thuộc đồ thị hàm số \(y = 3x\).
Vậy đường thẳng \(OA\) là đồ thị của hàm số \(y = 3x\).
b) Xét điểm \(M\,( - 2; - 6)\,\, \Rightarrow x = - 2;\,\,y = - 6\) , thay vào \(y = 3x\) ta được \( - 6 = 3.( - 2)\) (thỏa mãn).
Vậy điểm \(M{\kern 1pt} \,( - 2;\, - 6)\) thuộc đồ thị hàm số \(y = 3x\).
Bài 3:
\(\begin{array}{l}a)\;\dfrac{1}{3} + \dfrac{2}{3}:x = - 2\\ \Leftrightarrow \dfrac{2}{3}:x = - 2 - \dfrac{1}{3}\\ \Leftrightarrow \dfrac{2}{3}:x = \dfrac{{ - 7}}{3}\\ \Leftrightarrow x = \dfrac{2}{3}:\dfrac{{ - 7}}{3}\\ \Leftrightarrow x = \dfrac{{ - 2}}{7}\end{array}\)
Vậy \(x = \dfrac{{ - 2}}{7}\).
b) \(7x = 3y\) và \(2x - y = 16\)
Ta có \(7x = 3y\,\, \Rightarrow \,\,\dfrac{x}{3} = \dfrac{y}{7}\,\, \Rightarrow \dfrac{{2x}}{6} = \dfrac{y}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\dfrac{{2x}}{6} = \dfrac{y}{7} = \dfrac{{2x - y}}{{6 - 7}} = \dfrac{{16}}{{ - 1}} = - 16\\ \Rightarrow \dfrac{{2x}}{6} = - 16\,\, \Rightarrow \dfrac{x}{3} = - 16\, \Rightarrow x = - 16.3 = - 48\\\,\,\,\,\,\,\,\dfrac{y}{7} = - 16\,\,\, \Rightarrow y = - 16.7 = - 112\end{array}\)
Vậy \(x = - 48\) và \(y = - 112\).
c) Gọi \(x\) là thời gian cần thiết để người đó đánh được \(800\) từ \((x > 0)\).
Vì thời gian và số từ đánh được là hai đại lượng tỉ lệ thuận nên ta có:
\(\dfrac{x}{{2,5}} = \dfrac{{800}}{{160}}\,\,\, \Rightarrow x = \dfrac{{800.2,5}}{{160}} = 12,5\,\,\)
Vậy cần \(12,5\) phút để người đó đánh được \(800\) từ.
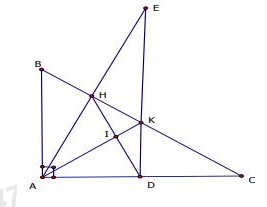
Bài 4:
|
GT |
\(\Delta ABC\)vuông tại \(A,\,\,\angle B = {60^0},\,\,AH \bot BC\) tại \(H\) ; \(D \in AC,\,\,AD = AH,\,\,I\) là trung điểm của \(HD\) \(AI\) cắt \(HC\) tại \(K\); \(E\) thuộc tia đối của tia \(HA;\,\,HE = AH\) |
|
|
KL |
a) \(\angle HAB = ?\) b) \(\Delta AHI = \Delta ADI\,;\,\,\,AI \bot HD\) c) \(\Delta AHK = \Delta ADK\,;\,\,\,AB//KD\) d) \(H\) là trung điểm của \(BK\) ; ba điểm \(D,K,E\) thẳng hàng |
|
a) Xét \(\Delta AHB\)vuông tại\(H\) ta có:
\(\angle HBA + \angle HAB = {90^0}\) (hai góc phụ nhau)
\( \Rightarrow \angle HAB = {90^0} - \angle HBA = {90^0} - {60^0} = {30^0}\)
Vậy \(\angle HAB = {30^0}\)
b) Xét \(\Delta AHI\) và \(\Delta ADI\) ta có:
\(AH = AD\,\,(gt)\)
\(IH = ID\)(do \(I\) là trung điểm của \(HD\))
\(AI\) là cạnh chung
Vậy \(\Delta AHI = \Delta ADI\,\,(c.c.c)\)
Suy ra \(\angle HIA = \angle DIA\) (\(2\) góc tương ứng)
Mà \(\angle HIA + \angle DIA = {180^0}\) (\(2\) góc kề bù)
\( \Rightarrow \,\angle HIA = \angle DIA = {90^0}\)
Do đó: \(AI \bot HD\,\) (đpcm)
c) Vì \(\Delta AHI = \Delta ADI\,\) (cm câu b)
\( \Rightarrow \angle HAK = \angle DAK\) (\(2\) góc tương ứng)
Xét \(\Delta AHK\) và \(\Delta ADK\) ta có:
\(AH = AD\,\,(gt)\)
\(\angle HAK = \angle DAK\) (cmt)
\(AK\) là cạnh chung
Vậy \(\Delta AHK = \Delta ADK\,\,(c.g.c)\)
\( \Rightarrow \angle AHK = \angle ADK = {90^0}\) (\(2\) góc tương ứng)
\( \Rightarrow KD \bot AC\)
Mà \(BA \bot AC\) (do \(\Delta ABC\) vuông tại \(A\))
Suy ra \(AB//KD\) (đpcm)
d) Ta có:
\(\begin{array}{l}\angle BAH + \angle HAD = \angle BAD = {90^0}\\ \Rightarrow \angle HAD = {90^0} - \angle BAH = {90^0} - {30^0} = {60^0}\end{array}\)
Lại có \(\angle HAK = \angle DAK\)(cmt)
Suy ra \(\angle HAK = \angle DAK = {30^0}\)
Theo chứng câu ta có \(\angle HAB = {30^0}\).
Vậy \(\angle HAB = \angle HAK\)
+) Xét hai tam giác vuông tại \(H\) là \(\Delta ABH\) và \(\Delta AKH\) ta có:
\(\angle BHA = \angle KHA = {90^0}\)
\(AH\) là cạnh chung
\(\angle HAB = \angle HAK\)(cmt)
Vậy \(\Delta ABH = \Delta AKH\,\,(c.g.c)\)
\( \Rightarrow BH = KH\) (\(2\) cạnh tương ứng)
+) Xét \(\Delta ABH\) và \(\Delta EKH\) ta có:
\(BH = KH\) (cmt)
\(\angle BHA = \angle KHE\)(\(2\) góc đối đỉnh)
\(AH = HE\,\) (gt)
Vậy \(\Delta ABH = \Delta EKH\,\,(c.g.c)\)
\( \Rightarrow \angle ABH = \angle EKH\) (\(2\) góc tương ứng)
Mà \(\angle ABH\) và \(\angle EKH\) là hai góc so le trong
Suy ra \(AB//EK\)(dấu hiệu nhận biết hai đường thẳng song song)
Mà \(AB//KD\) (cm câu c)
Theo tiên đề Ơ-clit thì đường thẳng \(EK\) trùng với đường thẳng \(KD\).
Do đó ba điểm \(D,K,E\) thẳng hàng.
Bài 5:
a) Ta có:
\(\begin{array}{l}\;\;\dfrac{1}{{1.3}} + \dfrac{1}{{3.5}} + \dfrac{1}{{5.7}} + ... + \dfrac{1}{{19.21}}\\ = \dfrac{1}{2} \cdot \left( {\dfrac{2}{{1.3}} + \dfrac{2}{{3.5}} + \dfrac{2}{{5.7}} + ... + \dfrac{2}{{19.21}}} \right)\\ = \dfrac{1}{2} \cdot \left( {1 - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{5} + \dfrac{1}{5} - \dfrac{1}{7} + ... + \dfrac{1}{{19}} - \dfrac{1}{{21}}} \right)\\ = \dfrac{1}{2} \cdot \left( {1 - \dfrac{1}{{21}}} \right)\\ = \dfrac{1}{2} \cdot \dfrac{{20}}{{21}} = \dfrac{{10}}{{21}}\end{array}\)
b) Ta có:
\(\begin{array}{l}A = \dfrac{1}{{1.3}} + \dfrac{1}{{3.5}} + \dfrac{1}{{5.7}} + ... + \dfrac{1}{{(2n - 1)(2n + 1)}}\\\,\,\,\, = \dfrac{1}{2} \cdot \left( {\dfrac{2}{{1.3}} + \dfrac{2}{{3.5}} + \dfrac{2}{{5.7}} + ... + \dfrac{2}{{(2n - 1)(2n + 1)}}} \right)\\\,\,\,\, = \dfrac{1}{2} \cdot \left( {1 - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{5} + ... + \dfrac{1}{{2n - 1}} - \dfrac{1}{{2n + 1}}} \right)\\\,\,\,\, = \dfrac{1}{2} \cdot \left( {1 - \dfrac{1}{{2n + 1}}} \right)\end{array}\)
Lại có\(1 - \dfrac{1}{{2n + 1}} < 1\)nên suy ra \(A < \dfrac{1}{2}.1\), hay \(A < \dfrac{1}{2}\) (đpcm).
Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 7 tại Tuyensinh247.com
Loigiaihay.com












Danh sách bình luận