Đề thi học kì 1 Toán 8 - Đề số 1 - Kết nối tri thức
Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên
Phần trắc nghiệm (3 điểm) Câu 1: Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
Đề bài
Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
-
A.
\(14{x^2}y + 10{x^3}{y^2}\).
-
B.
\( - 14{x^2}y + 10{x^3}{y^2}\).
-
C.
\(6{x^2}y - 10{x^3}{y^2}\).
-
D.
\( - 6{x^2}y + 10{x^3}{y^2}\).
Giá trị của đa thức \(xy + 2{x^2}{y^3} - {x^4}y\) tại x = y = -1 là :
-
A.
3.
-
B.
1.
-
C.
-1.
-
D.
0.
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
1. \(\left( {x + y} \right)\left( {x - y} \right)\)
2. \({x^2} - 2xy + {y^2}\)
3. \({\left( {x + y} \right)^2}\)
4. \(\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\)
a. \({x^3} + {y^3}\)
b. \({x^2} + 2xy + {y^2}\)
c. \({x^2} - {y^2}\)
d. \({\left( {x - y} \right)^2}\)
Tam giác ABC có đường trung tuyến AM = 2cm; cạnh BC = 4 cm. khi đó:
-
A.
Tam giác ABC vuông tại A
-
B.
Tam giác ABC vuông tại B
-
C.
Tam giác ABC vuông tại C
-
D.
Cả 3 câu trên đều sai
Một tứ giác có nhiều nhất :
-
A.
1 góc nhọn.
-
B.
2 góc nhọn
-
C.
3 góc nhọn
-
D.
4 góc nhọn
Hình bình hành là một tứ giác có:
-
A.
Hai đường chéo bằng nhau.
-
B.
Hai đường chéo vuông góc.
-
C.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
-
D.
Hai đường chéo bằng nhau và vuông góc với nhau.
-
A.
1,5cm
-
B.
4.5 cm
-
C.
6 cm
-
D.
3 cm
Cho tam giác ABC, vẽ MN//BC sao cho AN =\(\frac{1}{2}\)AB, M \( \in \) AB, N \( \in \) AC. Biết AN = 2cm, AM = 1cm, thì AC bằng:
-
A.
4cm
-
B.
6cm
-
C.
8cm
-
D.
10cm
Có bao nhiêu đường trung bình trong một tam giác?
-
A.
1 đường trung bình
-
B.
2 đường trung bình
-
C.
3 đường trung bình
-
D.
4 đường trung bình
Các món ăn yêu thích của học sinh lớp 8A ghi lại trong bảng sau :
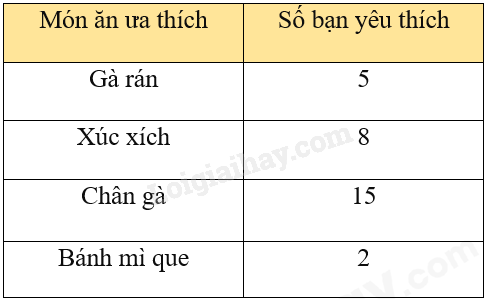
Dữ liệu định lượng (số liệu) trong bảng là :
-
A.
Món ăn ưa thích : Gà rán, xúc xích, chân gà, Bánh mì que.
-
B.
Số bạn yêu thích : 5; 8; 15; 2.
-
C.
Gà rán, xúc xích, chân gà, bánh mì que , 5, 8, 15, 2.
-
D.
Cả A, B, C đều đúng.
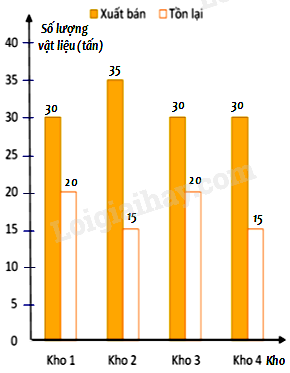
Một công ty kinh doanh vật liệu xây dựng có bốn kho hàng có 50 tấn hàng. Kế toán của công ty lập biểu đồ cột kép ở hình bên biểu diễn số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại trong mỗi kho sau tuần lễ kinh doanh đầu tiên.
Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép đó. Theo em, kế toán đã ghi nhầm số liệu ở kho nào ?
-
A.
Kho 1.
-
B.
Kho 2 và kho 4.
-
C.
Kho 1 và kho 3.
-
D.
Kho 4.
Lời giải và đáp án
Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
-
A.
\(14{x^2}y + 10{x^3}{y^2}\).
-
B.
\( - 14{x^2}y + 10{x^3}{y^2}\).
-
C.
\(6{x^2}y - 10{x^3}{y^2}\).
-
D.
\( - 6{x^2}y + 10{x^3}{y^2}\).
Đáp án : D
Sử dụng quy tắc tính với đa thức.
Ta có:
\(\begin{array}{l}4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\\ = \left( {4{x^2}y - 10{x^2}y} \right) + \left( {6{x^3}{y^2} + 4{x^3}{y^2}} \right)\\ = - 6{x^2}y + 10{x^3}{y^2}\end{array}\)
Giá trị của đa thức \(xy + 2{x^2}{y^3} - {x^4}y\) tại x = y = -1 là :
-
A.
3.
-
B.
1.
-
C.
-1.
-
D.
0.
Đáp án : D
Thay x = y = -1 vào đa thức rồi tính toán.
Thay x = y = -1 vào đa thức \(xy + 2{x^2}{y^3} - {x^4}y\) ta được
\(\begin{array}{l}\left( { - 1} \right).\left( { - 1} \right) + 2{\left( { - 1} \right)^2}.{\left( { - 1} \right)^3} - {\left( { - 1} \right)^4}\left( { - 1} \right)\\ = 1 - 2 + 1 = 0\end{array}\)
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
1. \(\left( {x + y} \right)\left( {x - y} \right)\)
2. \({x^2} - 2xy + {y^2}\)
3. \({\left( {x + y} \right)^2}\)
4. \(\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\)
a. \({x^3} + {y^3}\)
b. \({x^2} + 2xy + {y^2}\)
c. \({x^2} - {y^2}\)
d. \({\left( {x - y} \right)^2}\)
1. \(\left( {x + y} \right)\left( {x - y} \right)\)
c. \({x^2} - {y^2}\)
2. \({x^2} - 2xy + {y^2}\)
d. \({\left( {x - y} \right)^2}\)
3. \({\left( {x + y} \right)^2}\)
b. \({x^2} + 2xy + {y^2}\)
4. \(\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\)
a. \({x^3} + {y^3}\)
Sử dụng kiến thức về các hằng đẳng thức đáng nhớ.
- \(\left( {x + y} \right)\left( {x - y} \right) = {x^2} - {y^2} \Rightarrow \)1 – c.
- \({x^2} - 2xy + {y^2} = {\left( {x - y} \right)^2} \Rightarrow \) 2 – d.
- \({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2} \Rightarrow \) 3 – b.
- \(\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right) = {x^3} + {y^3} \Rightarrow \)4 – a.
Tam giác ABC có đường trung tuyến AM = 2cm; cạnh BC = 4 cm. khi đó:
-
A.
Tam giác ABC vuông tại A
-
B.
Tam giác ABC vuông tại B
-
C.
Tam giác ABC vuông tại C
-
D.
Cả 3 câu trên đều sai
Đáp án : A
Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông.
Ta có: AM = 2cm; BC = 4cm \( \Rightarrow AM = \frac{1}{2}BC\). Mà AM là đường trung tuyến ứng với cạnh BC nên AM là đường trung tuyến ứng với cạnh huyền BC hay tam giác ABC vuông tại A.
Một tứ giác có nhiều nhất :
-
A.
1 góc nhọn.
-
B.
2 góc nhọn
-
C.
3 góc nhọn
-
D.
4 góc nhọn
Đáp án : C
Áp dụng định lí tổng các góc của một tứ giác bằng \(360^0\).
- Nếu 4 góc trong tứ giác đều nhọn (nhỏ hơn \(90^0\)) => Tổng 4 góc < \(4.90^0\) = \(360^0\) => Vô lí vì tổng 4 góc trong tứ giác bằng \(360^0\).
- Nếu có 3 góc nhỏ hơn \(90^0\) ; 1 góc > \(90^0\) => Tổng 3 góc đó < 3.\(90^0\) = \(270^0\) => góc còn lại lớn hơn \(360^0- 270^0 = 90^0\) (thỏa mãn)
Vậy tứ giác có thể có nhiều nhất 3 góc nhọn.
Hình bình hành là một tứ giác có:
-
A.
Hai đường chéo bằng nhau.
-
B.
Hai đường chéo vuông góc.
-
C.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
-
D.
Hai đường chéo bằng nhau và vuông góc với nhau.
Đáp án : C
Ta sử dụng kiến thức về hình bình hành.
Hình bình hành là một tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên C đúng.
-
A.
1,5cm
-
B.
4.5 cm
-
C.
6 cm
-
D.
3 cm
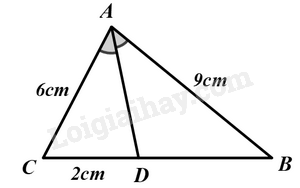
Đáp án : D
Sử dụng tính chất của đường phân giác trong tam giác.
Ta có AD là tia phân giác của góc A nên \(\frac{{AB}}{{BD}} = \frac{{AC}}{{CD}} \Leftrightarrow \frac{9}{{BD}} = \frac{6}{2} = 3\)
\( \Rightarrow BD = \frac{9}{3} = 3\)(cm)
Cho tam giác ABC, vẽ MN//BC sao cho AN =\(\frac{1}{2}\)AB, M \( \in \) AB, N \( \in \) AC. Biết AN = 2cm, AM = 1cm, thì AC bằng:
-
A.
4cm
-
B.
6cm
-
C.
8cm
-
D.
10cm
Đáp án : C
Áp dụng định lí Thalès để tính BC.
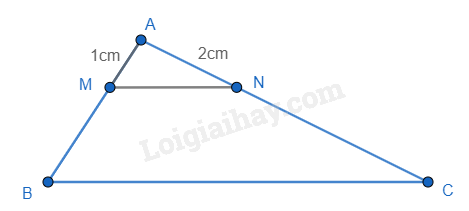
Vì AN = \(\frac{1}{2}\)AB nên AB = 2.AN = 2.2 = 4(cm).
Ta có MN // BC. Áp dụng định lí Thales, ta có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Leftrightarrow \frac{1}{4} = \frac{2}{{AC}} \Leftrightarrow AC = 4.2 = 8\) (cm).
Vậy AC = 8cm.
Có bao nhiêu đường trung bình trong một tam giác?
-
A.
1 đường trung bình
-
B.
2 đường trung bình
-
C.
3 đường trung bình
-
D.
4 đường trung bình
Đáp án : C
Sử dụng khái niệm đường trung bình.
Xét tam giác ABC bất kì. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.
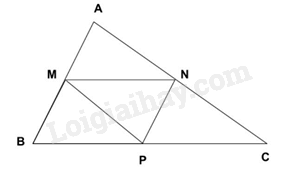
MN là đường trung bình của tam giác ABC.
NP là đường trung bình của tam giác ABC.
MP là đường trung bình của tam giác ABC.
Vậy có 3 đường trung bình trong một tam giác.
Các món ăn yêu thích của học sinh lớp 8A ghi lại trong bảng sau :

Dữ liệu định lượng (số liệu) trong bảng là :
-
A.
Món ăn ưa thích : Gà rán, xúc xích, chân gà, Bánh mì que.
-
B.
Số bạn yêu thích : 5; 8; 15; 2.
-
C.
Gà rán, xúc xích, chân gà, bánh mì que , 5, 8, 15, 2.
-
D.
Cả A, B, C đều đúng.
Đáp án : B
Dựa vào phân loại dữ liệu: Dữ liệu được chia thành hai loại: Dữ liệu định tính (dữ liệu không phải số) và dữ liệu định lượng (số liệu).
Dữ liệu định lượng (số liệu) trong bảng trên là dữ liệu Số bạn yêu thích : 5; 8; 15; 2.
Một công ty kinh doanh vật liệu xây dựng có bốn kho hàng có 50 tấn hàng. Kế toán của công ty lập biểu đồ cột kép ở hình bên biểu diễn số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại trong mỗi kho sau tuần lễ kinh doanh đầu tiên.
Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép đó. Theo em, kế toán đã ghi nhầm số liệu ở kho nào ?

-
A.
Kho 1.
-
B.
Kho 2 và kho 4.
-
C.
Kho 1 và kho 3.
-
D.
Kho 4.
Đáp án : D
Kiểm tra xem dữ liệu trong biểu đồ có cột nào chưa chính xác.
Vì mỗi kho hàng đều có 50 tấn hàng nên tổng số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại phải bằng 50 tấn. Mà cột kho 4, số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại là: 30 + 15 = 45 (tấn) nên số liệu ở kho 4 không đúng.
Sử dụng các hằng đẳng thức đáng nhớ.
a) \({(x + 1)^2} - \left( {x + 3} \right)\left( {x - 3} \right) - 10\)
\(\begin{array}{l} = {\left( {x + 1} \right)^2} - \left( {{x^2} - {3^2}} \right) - 10\\ = {x^2} + 2x + 1 - {x^2} + 9 - 10\\ = \left( {{x^2} - {x^2}} \right) + 2x + \left( {1 + 9 - 10} \right)\\ = 2x\end{array}\)
b) \(\left( {x + 5} \right)\left( {{x^2} - 5x + 25} \right) - x{\left( {x - 4} \right)^2} + 16x\)
\(\begin{array}{l} = {x^3} + {5^3} - x\left( {{x^2} - 8x + 16} \right) + 16x\\ = {x^3} + 125 - {x^3} + 8{x^2} - 16x + 16x\\ = 8{x^2} + 125\end{array}\)
c) \({\left( {x - 2y} \right)^3} - \left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) + 6{x^2}y\)
\(\begin{array}{l} = {\left( {x - 2y} \right)^3} - \left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) + 6{x^2}y\\ = {x^3} - 6{x^2}y + 12x{y^2} - 8{y^3} - \left( {{x^3} + 8{y^3}} \right) + 6{x^2}y\\ = {x^3} - 6{x^2}y + 12x{y^2} - 8{y^3} - {x^3} - 8{y^3} + 6{x^2}y\\ = \left( {{x^3} - {x^3}} \right) + \left( { - 6{x^2}y + 6{x^2}y} \right) + 12x{y^2} + \left( { - 8{y^3} - 8{y^3}} \right)\\ = 12x{y^2} - 16{y^3}\end{array}\)
Dựa vào các hằng đẳng thức đáng nhớ, phân tích đa thức thành nhân tử để tìm x.
a) \({\left( {x + 3} \right)^2} - \left( {x + 2} \right)\left( {x - 2} \right) = 4x + 17\)
\(\begin{array}{l}{x^2} + 6x + 9 - {x^2} + 4 = 4x + 17\\6x + 13 = 4x + 17\\6x - 4x = 17 - 13\\2x = 4\\x = 2\end{array}\)
Vậy x = 2.
b) \(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) = 1\)
\(\begin{array}{l}\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) = 1\\{x^3} - 27 - {x^3} + 4x = 1\\4x = 1 + 27\\4x = 28\\x = 7\end{array}\)
Vậy x = 7.
a) Dựa vào dữ liệu đề bài cho để điền vào bảng.
b) Điền số tương ứng vào biểu đồ.
a) Ta có bảng thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm:

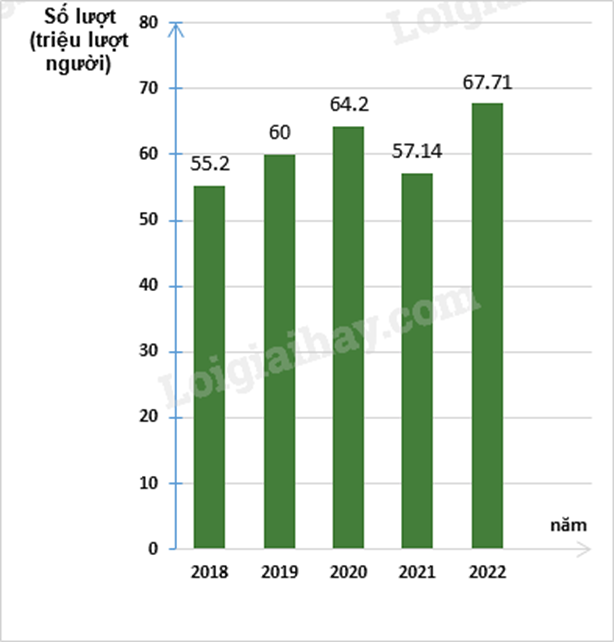
b) Biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên là:
a) Chứng minh tứ giác MNCP có hai cạnh đối song song và bằng nhau.
b) Chứng minh N là trực tâm của tam giác CMB nên NC\( \bot \)MB\( \Rightarrow \) MP\( \bot \)MB (MP // CN).
c) Chứng minh MI = PI, sử dụng bất đẳng thức tam giác để chứng minh PI – IJ < JP hay MI – IJ < JP.
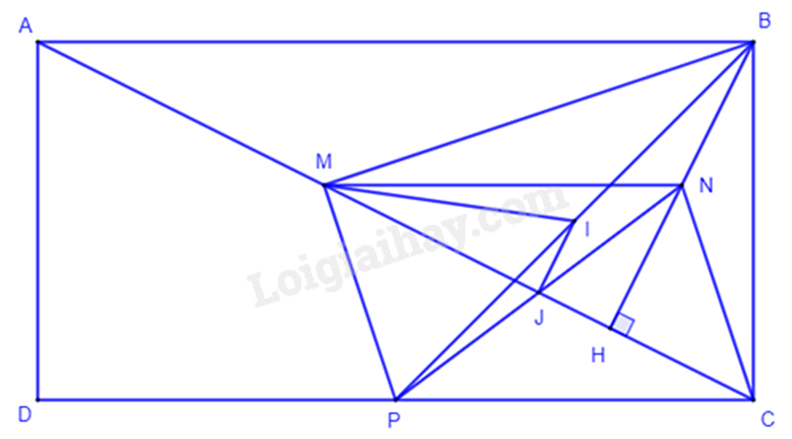
a) Xét tam giác AHB có:
M là trung điểm của AH
N là trung điểm của BH
Suy ra MN là đường trung bình của tam giác AHB. DO đó MN // AB và MN = \(\frac{1}{2}\)AB.
Vì P là trung điểm của CD nên CP = PD = \(\frac{1}{2}\)CD.
Mà AB // CD; AB = CD (ABCD là hình chữ nhật) nên CP = \(\frac{1}{2}\)AB.
Suy ra MN // CP (cùng song song với AB) và MN = CP (\(\frac{1}{2}\)AB).
Do đó tứ giác MNCP là hình bình hành (đpcm)
b) Do MN // AB (cmt) mà AB \( \bot \) BC (ABCD là hình chữ nhật) nên MN \( \bot \) BC.
Ta có BH \( \bot \) MC (gt)
Mà MN \( \cap \) BH tại N.
Suy ra N là trực tâm của tam giác CMB, do đó CN \( \bot \) BM.
Mà CN // PM (MNCP là hình bình hành)
Suy ra PM \( \bot \) BM (đpcm)
c) Xét tam giác PMB vuông tại M có I là trung điểm của BP nên MI là đường trung tuyến ứng với cạnh huyền của tam giác PMB suy ra MI = \(\frac{1}{2}\)BP = PI.
Xét tam giác PIJ, ta có: PI – IJ < JP hay MI – IJ < JP (đpcm).
Dựa vào hằng đẳng thức \({a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}\); \({a^2} - 2ab + {b^2} = {\left( {a - b} \right)^2}\) để tìm x, y.
Thay x, y vào biểu thức M để tính giá trị của biểu thức M.
Ta có:
\(\begin{array}{l}5{x^2} + 5{y^2} + 8xy - 2x + 2y + 2 = 0\\\left( {4{x^2} + 8xy + 4{y^2}} \right) + ({x^2} - 2x + 1) + ({y^2} + 2y + 1) = 0\\4{\left( {x + y} \right)^2} + {\left( {x-1} \right)^2} + {(y + 1)^2} = 0\left( * \right)\end{array}\)
Vì \(4{\left( {x + y} \right)^2} \ge 0;{\left( {x-1} \right)^2} \ge 0;{(y + 1)^2} \ge \;0\) với mọi x, y
Nên (*) xảy ra khi \(\left\{ \begin{array}{l}x + y = 0\\x - 1 = 0\\y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - y\\x = 1\\y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right.\).
Thay x = 1 và y = -1 vào biểu thức M, ta được:
\(M = {(1 - 1)^{2017}} + {(1 - 2)^{2018}} + {( - 1 + 1)^{2019}} = {\left( { - 1} \right)^{2018}} = 1\) .
Vậy M = 1 .
Phần trắc nghiệm (3 điểm) Câu 1: Thu gọn đa thức (2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y) ta được:
Phần trắc nghiệm (3 điểm) Câu 1: Kết quả của phép tính (xy + 5)(xy – 1) là:
Phần trắc nghiệm (3 điểm) Câu 1: Kết quả thương của phép chia (left( 3x{{y}^{2}}-2{{x}^{2}}y+{{x}^{3}} right):left( -frac{1}{2}x right)) là :
Phần trắc nghiệm (3 điểm) Câu 1: Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
A. NỘI DUNG ÔN TẬP Đại số 1. Các phép toán cộng, trừ, nhân, chia đa thức nhiều biến.
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |




 b) Hãy hoàn thiện biểu đồ ở hình bên để nhận được biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên.
b) Hãy hoàn thiện biểu đồ ở hình bên để nhận được biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên.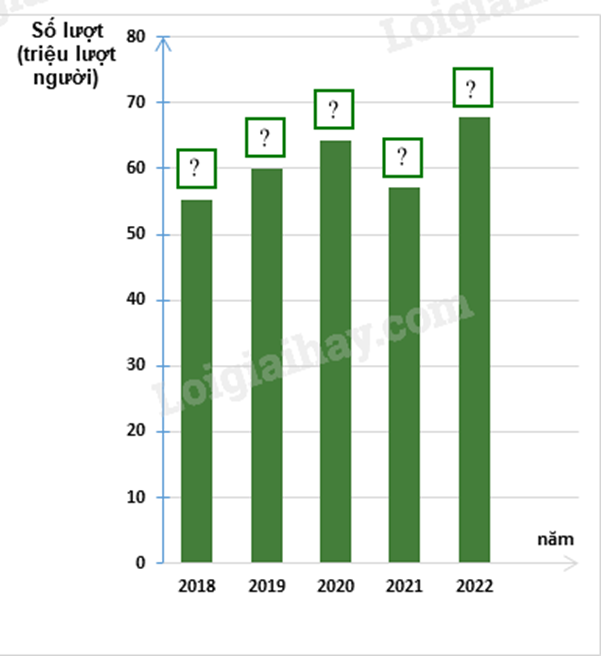






Danh sách bình luận