Đề thi học kì 2 Toán 8 Kết nối tri thức - Đề số 7
Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Điều kiện xác định của phân thức \(\frac{{x - 5}}{{{x^2} - 4}}\) là:
-
A.
\(x \ne 4\).
-
B.
\(x \ne 2\).
-
C.
\(x \ne - 2\).
-
D.
\(x \ne 2,x \ne - 2\).
Phân thức \(\frac{{2xy}}{{3{x^2}y}}\) bằng với phân thức nào trong các phân thức sau?
-
A.
\(\frac{{2y}}{{3x}}\).
-
B.
\(\frac{{2y}}{{5x}}\).
-
C.
\(\frac{{3y}}{{2x}}\).
-
D.
\(\frac{2}{{3x}}\).
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
-
A.
\({y^2} + 8x - 2022 = 0\).
-
B.
\(3x + 6 = 0\).
-
C.
\(3x - 2y - 9 = 0\).
-
D.
\(2{x^2} - 4 = 0\).
Gọi \(x\) (km) là chiều dài quãng đường AB. Biểu thức biểu thị vận tốc một xe đạp đi từ A đến B trong 5 giờ là
-
A.
\(\frac{x}{5}\).
-
B.
\(5 + x\).
-
C.
\(5 - x\).
-
D.
\(5x\).
Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
-
A.
\(y = {x^2} + 1\).
-
B.
\(y = 2\sqrt x + 1\).
-
C.
\(y = \frac{2}{3} - 2x\).
-
D.
\(y = 1 - \frac{1}{x}\).
Biết rằng đồ thị hàm số \(y = 2x + 1\) và đồ thị hàm số \(y = ax + 3\) là hai đường thẳng song song. Khi đó hệ số \(a\) bằng:
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
-2.
Chọn ngẫu nhiên một số tự nhiên có một chữ số. Số kết quả có thể xảy ra là:
-
A.
7.
-
B.
8.
-
C.
9.
-
D.
10.
Gieo một con xúc xắc cân đối đồng chất. Gọi B là biến cố: “Gieo được mặt có số chấm là số chẵn”. Xác suất của biến cố B là
-
A.
\(\frac{1}{2}\).
-
B.
\(\frac{1}{6}\).
-
C.
\(\frac{1}{3}\).
-
D.
\(\frac{2}{3}\).
Cho \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat A = 50^\circ ,\widehat B = 60^\circ ,\widehat D = 50^\circ ,\widehat E = 70^\circ \) thì
-
A.
$\Delta ABC\backsim \Delta DEF$.
-
B.
$\Delta ABC\backsim \Delta DFE$.
-
C.
$\Delta ABC\backsim \Delta EDF$.
-
D.
$\Delta ABC\backsim \Delta FED$.
Cho hình sau. Biết Hình 1 đồng dạng phối cảnh với Hình 2 với tỉ số đồng dạng là 2. Khi đó tỉ số nào sau đây là đúng?
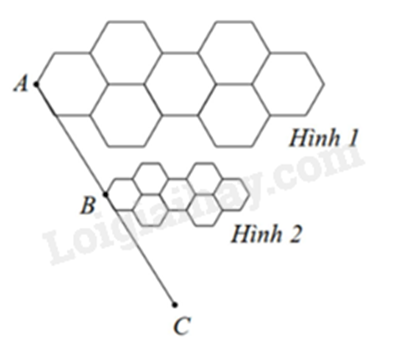
-
A.
\(\frac{{AB}}{{BC}} = 2\).
-
B.
\(\frac{{AB}}{{AC}} = 2\).
-
C.
\(\frac{{AC}}{{AB}} = 2\).
-
D.
\(\frac{{BC}}{{AB}} = 2\).
Cho các miếng bìa sau.
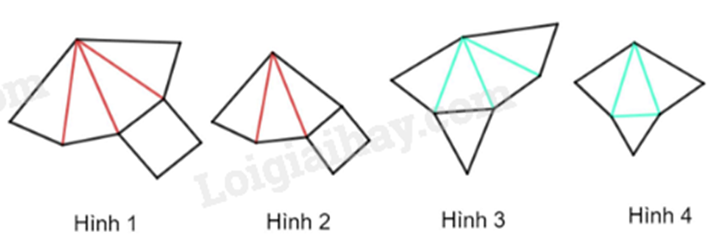
Miếng bìa nào sau khi gấp và dán lại thì được một hình chóp tứ giác đều?
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Diện tích xung quanh của hình chóp tam giác đều bằng
-
A.
nửa chu vi đáy nhân với đường cao.
-
B.
chu vi đáy nhân với trung đoạn.
-
C.
nửa chu vi đáy nhân với trung đoạn.
-
D.
chu vi đáy nhân với chiều cao.
Cho hàm số \(\left( d \right):y = \left( {2 - m} \right)x + 3m - 1\).
a) Điều kiện để hàm số trên là hàm số bậc nhất là \(m = 2\).
b) Với \(m = - 1\) thì đồ thị hàm số \(\left( d \right)\) đi qua điểm \(A\left( {0;4} \right)\).
c) Để \(\left( d \right)\) song song với \(\left( {d'} \right):y = - x + m - 3\) thì \(m = 3\).
d) Để \(\left( d \right)\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung thì \(m = 1\).
Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Tết thiếu nhi, cô giáo đã chọn ra 10 học sinh gồm: 4 học sinh nữ là Hoa, Mai, Linh, My; 6 học sinh nam là Cường, Hùng, Nguyên, Kiên, Phúc, Hoàng. Chọn ngẫu nhiên một học sinh trong nhóm các học sinh tập múa trên.
a) Các kết quả có thể xảy ra là 10.
b) Có 6 kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ”.
c) Xác suất của biến cố “Học sinh được chọn là nam” là 0,6.
d) Xác suất của biến cố “Học sinh được chọn là nam và có tên bắt đầu bằng chữ H” là 0,2.
Xác định hệ số góc của đường thẳng đi qua hai điểm A (1;2) và B (3;4).
Đáp án:
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ ghi một trong các số sau: 1; 2; 3; …; 49; 50, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3”.
(Kết quả ghi dưới dạng số thập phân)
Đáp án:
Gấp mảnh giấy hình chữ nhật như hình vẽ sau đây sao cho điểm D trùng với điểm E, là một điểm nằm trên cạnh BC. Biết rằng AD = 10 cm, AB = 8cm.
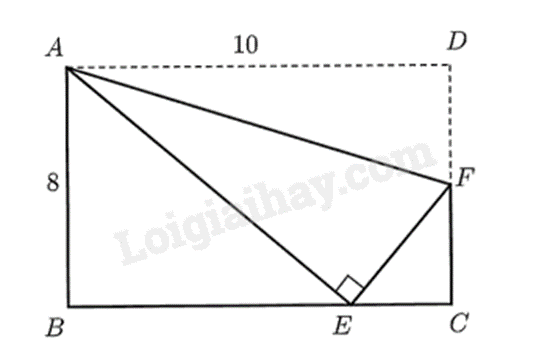
Hỏi độ dài của cạnh EC bằng bao nhiêu centimet?
Đáp án:
Một bể kính hình hộp chữ nhật có hai cạnh đáy là 60 cm và 30 cm. Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270c{m^2}\), chiều cao 30 cm. Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mức nước là 60 cm.
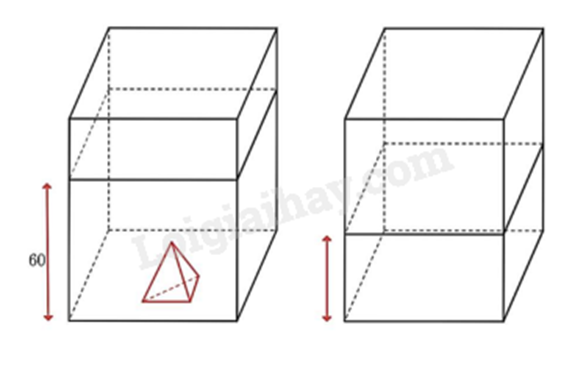
Khi lấy khối đá ra thì mực nước của bể cao bao nhiêu centimet? (Kết quả ghi dưới dạng số thập phân)
Đáp án:
Lời giải và đáp án
Điều kiện xác định của phân thức \(\frac{{x - 5}}{{{x^2} - 4}}\) là:
-
A.
\(x \ne 4\).
-
B.
\(x \ne 2\).
-
C.
\(x \ne - 2\).
-
D.
\(x \ne 2,x \ne - 2\).
Đáp án : D
Điều kiện xác định của phân thức \(\frac{A}{B}\) là \(B \ne 0\).
Điều kiện xác định của phân thức \(\frac{{x - 5}}{{{x^2} - 4}}\) là \({x^2} - 4 \ne 0\) hay \({x^2} \ne 4\) suy ra \(x \ne 2;x \ne - 2\).
Đáp án D
Phân thức \(\frac{{2xy}}{{3{x^2}y}}\) bằng với phân thức nào trong các phân thức sau?
-
A.
\(\frac{{2y}}{{3x}}\).
-
B.
\(\frac{{2y}}{{5x}}\).
-
C.
\(\frac{{3y}}{{2x}}\).
-
D.
\(\frac{2}{{3x}}\).
Đáp án : D
Rút gọn phân thức để tìm phân thức bằng với \(\frac{{2xy}}{{3{x^2}y}}\).
Ta có: \(\frac{{2xy}}{{3{x^2}y}} = \frac{2}{{3x}}\).
Đáp án D
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
-
A.
\({y^2} + 8x - 2022 = 0\).
-
B.
\(3x + 6 = 0\).
-
C.
\(3x - 2y - 9 = 0\).
-
D.
\(2{x^2} - 4 = 0\).
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\left( {a \ne 0} \right)\).
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\left( {a \ne 0} \right)\).
Do đó \(3x + 6 = 0\) là phương trình bậc nhất một ẩn.
Đáp án B
Gọi \(x\) (km) là chiều dài quãng đường AB. Biểu thức biểu thị vận tốc một xe đạp đi từ A đến B trong 5 giờ là
-
A.
\(\frac{x}{5}\).
-
B.
\(5 + x\).
-
C.
\(5 - x\).
-
D.
\(5x\).
Đáp án : A
Sử dụng công thức liên hệ giữa vận tốc, thời gian và quãng đường: \(v = \frac{S}{t}\).
Biểu thức biểu thị vận tốc của xe đạp đi từ A đến B là: \(\frac{x}{5}\).
Đáp án A
Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
-
A.
\(y = {x^2} + 1\).
-
B.
\(y = 2\sqrt x + 1\).
-
C.
\(y = \frac{2}{3} - 2x\).
-
D.
\(y = 1 - \frac{1}{x}\).
Đáp án : C
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\).
Hàm số \(y = \frac{2}{3} - 2x\) là hàm số bậc nhất.
Đáp án C
Biết rằng đồ thị hàm số \(y = 2x + 1\) và đồ thị hàm số \(y = ax + 3\) là hai đường thẳng song song. Khi đó hệ số \(a\) bằng:
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
-2.
Đáp án : B
Đồ thị hàm số \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau nếu \(a = a',b \ne b'\).
Vì đồ thị hàm số \(y = 2x + 1\) và đồ thị hàm số \(y = ax + 3\) là hai đường thẳng song song nên hệ số \(a = 2\) và \(1 \ne 3\).
Đáp án B
Chọn ngẫu nhiên một số tự nhiên có một chữ số. Số kết quả có thể xảy ra là:
-
A.
7.
-
B.
8.
-
C.
9.
-
D.
10.
Đáp án : D
Liệt kê các số tự nhiên có một chữ số, ta được số kết quả có thể xảy ra.
Có 10 số tự nhiên có một chữ số là: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Vậy có 10 kết quả có thể xảy ra.
Đáp án D
Gieo một con xúc xắc cân đối đồng chất. Gọi B là biến cố: “Gieo được mặt có số chấm là số chẵn”. Xác suất của biến cố B là
-
A.
\(\frac{1}{2}\).
-
B.
\(\frac{1}{6}\).
-
C.
\(\frac{1}{3}\).
-
D.
\(\frac{2}{3}\).
Đáp án : A
Xác định số kết quả có thể.
Xác định các mặt có số chấm chẵn, ta được số các kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể (tổng số thẻ).
Xúc xắc có 6 mặt: 1; 2; 3; 4; 5; 6 nên có 6 kết quả có thể khi gieo con xúc xắc.
Các mặt có số chấm chẵn là: 2; 4; 6 nên có 3 kết quả thuận lợi cho biến cố B.
Xác suất của biến cố B là \(\frac{3}{6} = \frac{1}{2}\).
Đáp án A
Cho \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat A = 50^\circ ,\widehat B = 60^\circ ,\widehat D = 50^\circ ,\widehat E = 70^\circ \) thì
-
A.
$\Delta ABC\backsim \Delta DEF$.
-
B.
$\Delta ABC\backsim \Delta DFE$.
-
C.
$\Delta ABC\backsim \Delta EDF$.
-
D.
$\Delta ABC\backsim \Delta FED$.
Đáp án : B
Sử dụng định lí tổng ba góc trong tam giác để tính \(\widehat C\).
Từ đó chứng minh hai tam giác đồng dạng theo trường hợp góc – góc.
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) suy ra \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 50^\circ - 60^\circ = 70^\circ \).
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
\(\widehat A = \widehat D\left( { = 50^\circ } \right)\)
\(\widehat C = \widehat E\left( { = 70^\circ } \right)\)
nên $\Delta ABC\backsim \Delta DFE\left( g.g \right)$
Đáp án B
Cho hình sau. Biết Hình 1 đồng dạng phối cảnh với Hình 2 với tỉ số đồng dạng là 2. Khi đó tỉ số nào sau đây là đúng?

-
A.
\(\frac{{AB}}{{BC}} = 2\).
-
B.
\(\frac{{AB}}{{AC}} = 2\).
-
C.
\(\frac{{AC}}{{AB}} = 2\).
-
D.
\(\frac{{BC}}{{AB}} = 2\).
Đáp án : C
Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự): Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh và với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(\frac{{OM'}}{{OM}} = k\).
Vì Hình 1 đồng dạng phối cảnh với Hình 2 với tỉ số đồng dạng là 2 nên ta có: \(\frac{{AC}}{{AB}} = 2\).
Đáp án C
Cho các miếng bìa sau.

Miếng bìa nào sau khi gấp và dán lại thì được một hình chóp tứ giác đều?
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : A
Hình chóp tứ giác đều có 4 mặt bên là tam giác cân và đáy là hình vuông.
Vì hình chóp tứ giác đều có 4 mặt bên nên Hình 1 khi gấp và dán lại thì được một hình chóp tứ giác đều.
Đáp án A
Diện tích xung quanh của hình chóp tam giác đều bằng
-
A.
nửa chu vi đáy nhân với đường cao.
-
B.
chu vi đáy nhân với trung đoạn.
-
C.
nửa chu vi đáy nhân với trung đoạn.
-
D.
chu vi đáy nhân với chiều cao.
Đáp án : C
Dựa vào kiến thức về diện tích xung quanh của hình chóp tam giác đều.
Diện tích xung quanh của hình chóp bằng nửa chu vi đáy nhân với trung đoạn.
Đáp án C
Cho hàm số \(\left( d \right):y = \left( {2 - m} \right)x + 3m - 1\).
a) Điều kiện để hàm số trên là hàm số bậc nhất là \(m = 2\).
b) Với \(m = - 1\) thì đồ thị hàm số \(\left( d \right)\) đi qua điểm \(A\left( {0;4} \right)\).
c) Để \(\left( d \right)\) song song với \(\left( {d'} \right):y = - x + m - 3\) thì \(m = 3\).
d) Để \(\left( d \right)\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung thì \(m = 1\).
a) Điều kiện để hàm số trên là hàm số bậc nhất là \(m = 2\).
b) Với \(m = - 1\) thì đồ thị hàm số \(\left( d \right)\) đi qua điểm \(A\left( {0;4} \right)\).
c) Để \(\left( d \right)\) song song với \(\left( {d'} \right):y = - x + m - 3\) thì \(m = 3\).
d) Để \(\left( d \right)\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung thì \(m = 1\).
a) Điều kiện để hàm số \(y = ax + b\) là hàm số bậc nhất là \(a \ne 0\).
b) Thay \(m = - 1\) vào hàm số. Thay toạ độ điểm A vào đồ thị hàm số để kiểm tra xem điểm \(A\left( {0;4} \right)\) có thuộc đồ thị hàm số hay không.
c) Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song khi \(a = a',b \ne b'\).
d) Điểm thuộc trục tung thì có hoành độ bằng 0.
Thay \(x = 0\) vào (d”) để tìm \(y\).
Từ đó thay toạ độ giao điểm vào (d) để tìm m.
a) Đúng
Điều kiện để hàm số trên là hàm số bậc nhất là \(2 - m \ne 0\) suy ra \(m \ne 2\).
b) Sai
Với \(m = - 1\), ta được \(y = \left[ {2 - \left( { - 1} \right)} \right]x + 3\left( { - 1} \right) - 1 = 3x - 4\)
Do đó \(\left( d \right):y = 3x - 4\).
Thay \(x = 0,y = 4\) vào \(y = 3x - 4\), ta được: \(3.0 - 4 = 4\) hay \( - 4 = 4\) (vô lí)
Do đó với \(m = - 1\) thì đồ thị hàm số \(\left( d \right)\) không đi qua điểm \(A\left( {0;4} \right)\).
c) Đúng
Để đường thẳng \(\left( d \right):y = \left( {2 - m} \right)x + 3m - 1\) song song với \(\left( {d'} \right):y = - x + m - 3\) thì:
\(2 - m = - 1\) và \(3m - 1 \ne m - 3\)
\(m = 2 + 1\) \(3m - m \ne - 3 + 1\)
\(m = 3\) \(2m \ne - 2\)
\(m \ne - 1\)
Do đó \(m = 3\).
d) Đúng
Với \(x = 0\) thì \(y = - 0 + 2 = 2\) nên \(\left( {d''} \right):y = - x + 2\) cắt trục tung tại điểm có tung độ là 2.
Vì \(\left( d \right):y = \left( {2 - m} \right)x + 3m - 1\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung nên giao điểm của hai đường thẳng là điểm \(\left( {0;2} \right)\).
Thay \(x = 0;y = 2\) vào \(\left( d \right):y = \left( {2 - m} \right)x + 3m - 1\), ta được:
\(\begin{array}{l}2 = \left( {2 - m} \right).0 + 3m - 1\\2 = 3m - 1\\3m = 3\\m = 1\end{array}\)
Vậy để \(\left( d \right)\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung thì \(m = 1\).
Đáp án: ĐSĐĐ
Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Tết thiếu nhi, cô giáo đã chọn ra 10 học sinh gồm: 4 học sinh nữ là Hoa, Mai, Linh, My; 6 học sinh nam là Cường, Hùng, Nguyên, Kiên, Phúc, Hoàng. Chọn ngẫu nhiên một học sinh trong nhóm các học sinh tập múa trên.
a) Các kết quả có thể xảy ra là 10.
b) Có 6 kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ”.
c) Xác suất của biến cố “Học sinh được chọn là nam” là 0,6.
d) Xác suất của biến cố “Học sinh được chọn là nam và có tên bắt đầu bằng chữ H” là 0,2.
a) Các kết quả có thể xảy ra là 10.
b) Có 6 kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ”.
c) Xác suất của biến cố “Học sinh được chọn là nam” là 0,6.
d) Xác suất của biến cố “Học sinh được chọn là nam và có tên bắt đầu bằng chữ H” là 0,2.
a) Kết quả có thể là tổng số học sinh.
b) Kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ” là số các bạn học sinh nữ.
c) Kết quả thuận lợi cho biến cố “Học sinh được chọn là nam” là số các bạn học sinh nam.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
d) Xác định số kết quả thuận lợi cho biến cố “Học sinh được chọn là nam và có tên bắt đầu bằng chữ H”.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
a) Đúng
Có 10 kết quả có thể xảy ra khi chọn ngẫu nhiên một học sinh trong nhóm tập, đó là: Hoa, Mai, Linh, My, Cường, Hùng, Nguyên, Kiên, Phúc, Hoàng.
b) Sai
Số kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ” là 4 gồm Hoa, Mai, Linh, My.
c) Đúng
Số kết quả thuận lợi cho biến cố “Học sinh được chọn là nam” là 6.
Do đó, xác suất của biến cố “Học sinh được chọn là nam” là: \(\frac{6}{{10}} = 0,6\).
d) Sai
Số kết quả thuận lợi cho biến cố “Học sinh được chọn là nam và có tên bằng đầu bằng chữ H” là 2, đó là: Hùng; Hoàng.
Do đó xác suất của biến cố “Học sinh được chọn là nam và có tên bằng đầu bằng chữ H” là: \(\frac{2}{{10}} = 0,2\).
Đáp án: ĐSĐS
Xác định hệ số góc của đường thẳng đi qua hai điểm A (1;2) và B (3;4).
Đáp án:
Đáp án:
Gọi đường thẳng cần tìm là \(\left( d \right):y = ax + b\left( {a \ne 0} \right)\).
Thay lần lượt toạ độ của A, B vào hàm số và chuyển b sang 1 vế.
Từ đó ta được một phương trình bậc nhất ẩn a.
Giải phương trình ẩn a để tìm a.
Gọi đường thẳng cần tìm là \(\left( d \right):y = ax + b\left( {a \ne 0} \right)\).
Vì \(A\left( {1;2} \right) \in \left( d \right)\) nên \(2 = a + b\), suy ra \(b = 2 - a\) (1).
Vì \(B\left( {3;4} \right) \in \left( d \right)\) nên \(4 = 3a + b\), suy ra \(b = 4 - 3a\) (2)
Từ (1) và (2) suy ra:
\(2 - a = 4 - 3a\)
\(\begin{array}{l}3a - a = 4 - 2\\2a = 2\\a = 1\end{array}\)
Vậy hệ số góc của đường thẳng đó là 1.
Đáp án: 1
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ ghi một trong các số sau: 1; 2; 3; …; 49; 50, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3”.
(Kết quả ghi dưới dạng số thập phân)
Đáp án:
Đáp án:
Xác định số kết quả có thể.
Xác định các kết quả thuận lợi cho biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3”.
+ Liệt kê các số là bình phương của một số.
+ Xác định các số chia hết cho 3 trong các số đó.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
Các kết quả có thể xảy ra khi rút ngẫu nhiên một thẻ trong hộp là 50.
Kết quả thuận lợi cho biến cố “Thẻ được rút ra là bình phương của một số” là: 1; 4; 9; 16; 25; 36; 49.
Trong các số trên, các số chia hết cho ba là: 9; 36.
Suy ra, có 2 kết quả thuận lợi cho biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3”.
Vậy xác suất của biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3” là: \(\frac{2}{{50}} = \frac{1}{{25}} = 0,04\).
Đáp án: 0,04
Gấp mảnh giấy hình chữ nhật như hình vẽ sau đây sao cho điểm D trùng với điểm E, là một điểm nằm trên cạnh BC. Biết rằng AD = 10 cm, AB = 8cm.

Hỏi độ dài của cạnh EC bằng bao nhiêu centimet?
Đáp án:
Đáp án:
Do điểm D được gấp trùng với điểm E nên tính được AE.
Áp dụng định lí Pythagore vào tam giác AEB vuông tại B để tính BE.
Vì ABCD là hình chữ nhật nên tính được độ dài BC, từ đó tính được EC.
Do điểm D được gấp trùng với điểm E nên ta có \(AD = AE = 10cm\).
Áp dụng định lí Pythagore vào tam giác AEB vuông tại B, ta có:
\(A{B^2} + B{E^2} + A{E^2}\)
suy ra \(B{E^2} = A{E^2} - A{B^2} = {10^2} - {8^2} = 36\)
Do đó \(BE = \sqrt {36} = 6\left( {cm} \right)\)
Vì ABCD là hình chữ nhật nên \(AD = BC = 10cm\) nên \(BE + EC = BC\)
Suy ra \(EC = BC - BE = 10 - 6 = 4\left( {cm} \right)\).
Đáp án: 4
Một bể kính hình hộp chữ nhật có hai cạnh đáy là 60 cm và 30 cm. Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270c{m^2}\), chiều cao 30 cm. Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mức nước là 60 cm.

Khi lấy khối đá ra thì mực nước của bể cao bao nhiêu centimet? (Kết quả ghi dưới dạng số thập phân)
Đáp án:
Đáp án:
Áp dụng công thức tính thể tích hình chóp để tính thể tích khối đá.
Áp dụng công thức tính thể tích hình hộp chữ nhật để thể tích nước có khối đá bên trong.
Thể tích nước khi lấy khối đá ra = thể tích nước có khối đá bên trong – thể tích khối đá.
Tính diện tích đáy của bể.
Từ đó áp dụng công thức tính thể tích hình hộp chữ nhật để tính mực nước của bể.
Thể tích khối đá hình chóp tam giác đều là:
\({V_{hc}} = \frac{1}{3}S.h = \frac{1}{3}.270.30 = 2\,700\left( {c{m^3}} \right)\)
Thể tích nước có khối đá bên trong là:
\({V_{hhcn}} = 60.30.60 = 108\,000\left( {c{m^3}} \right)\)
Do đó thể tích nước khi lấy khối đá ra là:
\({V_{hhcn}} - {V_{hc}} = 108\,000 - 2\,700 = 105\,300\left( {c{m^3}} \right)\)
Diện tích đáy của bể hình hộp chữ nhật là:
\(60.30 = 1\,800\left( {c{m^2}} \right)\)
Vậy khi lấy khối đá ra thì mực nước của bể là: \(105\,300:1\,800 = 58,5\left( {cm} \right)\)
Đáp án: 58,5
Gọi số tấn thóc thu hoạch theo dự định là \(x\)(tấn) \((x > 0)\).
Biểu diễn số ngày thu hoạch hết số thóc theo dự định và số ngày thu hoạch hết số thóc thực tế, từ đó lập phương trình.
Giải phương trình, kiểm tra lại điều kiện và kết luận.
Gọi số tấn thóc thu hoạch theo dự định là \(x\)(tấn) \((x > 0)\).
Khi đó số ngày thu hoạch hết số thóc theo dự định là: \(\frac{x}{{20}}\) (ngày)
Số tấn thóc thực tế thu hoạch được là: \(x + 10\) (tấn)
Số tấn thóc thực tế mỗi ngày thu hoạch được là \(20 + 6 = 26\) (tấn)
Số ngày thu hoạch hết số thóc theo thực tế là: \(\frac{{x + 10}}{{26}}\) ngày
Vì hợp tác xã hoàn thành kế hoạch trước 1 ngày nên ta có phương trình:
\(\frac{x}{{20}} - 1 = \frac{{x + 10}}{{26}}\)
Giải phương trình:
\(\frac{x}{{20}} - 1 = \frac{{x + 10}}{{26}}\)
\(\frac{{13x}}{{20}} - \frac{{260}}{{260}} = \frac{{10\left( {x + 10} \right)}}{{26}}\)
\(\frac{{13x - 260}}{{260}} = \frac{{10x + 100}}{{260}}\)
\(13x - 260 = 10x + 100\)
\(13x - 10x = 100 + 260\)
\(3x = 360\)
\(x = 120\) (thỏa mãn)
Vậy số thóc theo dự định là 120 tấn.
a) Chứng minh \(\widehat {BAD} = \widehat {AHB} = 90^\circ \)
Từ đó chứng minh $\Delta ABD\backsim \Delta HBA$ (g.g)
b) Chứng minh $\Delta ABD\backsim \Delta HAD\left( g.g \right)$ suy ra \(\frac{{AD}}{{DH}} = \frac{{BD}}{{AD}}\) hay \(A{D^2} = BD.DH\)
Kết hợp đặc điểm của hình chữ nhật ta có AD = BC
Do đó \(B{C^2} = BD.DH\) (đpcm)
c) Chứng minh \(\Delta AIE\) cân tại A
Sử dụng tính chất tia phân giác cho DE và từ $\Delta ABD\backsim \Delta HAD$ suy ra \(\widehat {DBA} + \widehat {EDB} = \widehat {HAD} + \widehat {EDA}\)
Sử dụng tính chất góc ngoài cho \(\Delta AID\) và \(\Delta DEB\) để có \(\widehat {AIE} = \widehat {HAD} + \widehat {EDA}\) và \(\widehat {AEI} = \widehat {EBD} + \widehat {BDE}\)
Suy ra \(\widehat {AIE} = \widehat {AEI}\) nên \(\Delta AIE\) cân tại A.
Chứng minh \(A{E^2} = IH.EB\)
Từ \(\Delta AIE\) cân tại A có AE = AI
Kết hợp tính chất đường phân giác DI của tam giác \(\Delta ADH\) suy ra \(\frac{{IH}}{{IA}} = \frac{{DH}}{{DA}}\) nên \(\frac{{IH}}{{AE}} = \frac{{DH}}{{DA}}\)
Chứng minh \(\frac{{DH}}{{AD}} = \frac{{AD}}{{BD}}\) suy ra \(\frac{{IH}}{{AE}} = \frac{{AD}}{{BD}}\)
Kết hợp tính chất đường phân giác DE của tam giác \(\Delta ADB\) suy ra \(\frac{{AE}}{{EB}} = \frac{{AD}}{{BD}}\)
Suy ra \(\frac{{IH}}{{AE}} = \frac{{AE}}{{EB}}\), do đó \(A{E^2} = IH.EB\).
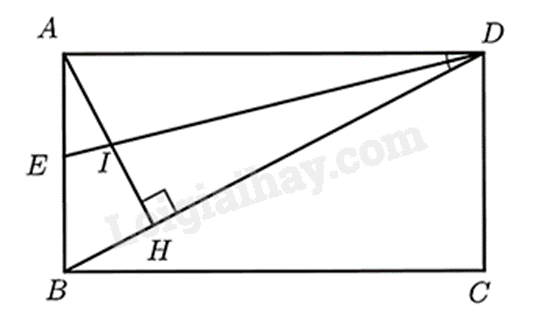
a) Vì ABCD là hình chữ nhật nên \(\widehat {BAD} = 90^\circ \).
Vì \(AH \bot BD\) tại H nên ta có: \(\widehat {BAD} = \widehat {AHB} = 90^\circ \).
Xét \(\Delta ABD\) và \(\Delta HBA\) có:
\(\widehat {BAD} = \widehat {AHB} = 90^\circ \) (cmt)
\(\widehat {ABD}\) chung
nên $\Delta ABD\backsim \Delta HBA$ (g.g) (đpcm)
b) Xét \(\Delta ABD\) và \(\Delta HAD\) có:
\(\widehat {BAD} = \widehat {AHD} = 90^\circ \)
\(\widehat {BDA}\) chung
nên $\Delta ABD\backsim \Delta HAD\left( g.g \right)$
suy ra \(\frac{{AD}}{{DH}} = \frac{{BD}}{{AD}}\) hay \(A{D^2} = BD.DH\)
Mà AD = BC (do ABCD là hình chữ nhật)
Do đó \(B{C^2} = BD.DH\) (đpcm)
c) Chứng minh \(\Delta AIE\) cân tại A
Vì DE là đường phân giác của tam giác ABD nên \(\widehat {ADE} = \widehat {EDB}\)
Vì $\Delta ABD\backsim \Delta HAD\left( cmt \right)$ nên \(\widehat {DBA} = \widehat {HAD}\) (hai góc tương ứng)
suy ra \(\widehat {DBA} + \widehat {EDB} = \widehat {HAD} + \widehat {EDA}\) (1)
Xét \(\Delta AID\) có \(\widehat {AIE} = \widehat {IAD} + \widehat {IDA} = \widehat {HAD} + \widehat {EDA}\) (tính chất góc ngoài) (2)
Xét \(\Delta DEB\) có \(\widehat {AEI} = \widehat {EBD} + \widehat {BDE}\) (tính chất góc ngoài) (3)
Từ (1), (2) và (3) suy ra \(\widehat {AIE} = \widehat {AEI}\).
Do đó \(\Delta AIE\) cân tại A (đpcm)
Chứng minh \(A{E^2} = IH.EB\)
\(\Delta AIE\) cân tại A suy ra AE = AI
Xét \(\Delta ADH\) có DI là đường phân giác nên \(\frac{{IH}}{{IA}} = \frac{{DH}}{{DA}}\), suy ra \(\frac{{IH}}{{AE}} = \frac{{DH}}{{DA}}\) (4)
Vì $\Delta ABD\backsim \Delta HAD\left( cmt \right)$ nên \(\frac{{DH}}{{AD}} = \frac{{AD}}{{BD}}\) (5)
Từ (4) và (5) suy ra \(\frac{{IH}}{{AE}} = \frac{{AD}}{{BD}}\) (6)
Xét \(\Delta ADB\) có DE là đường phân giác nên \(\frac{{AE}}{{EB}} = \frac{{AD}}{{BD}}\) (7)
Từ (6) và (7) suy ra \(\frac{{IH}}{{AE}} = \frac{{AE}}{{EB}}\), do đó \(A{E^2} = IH.EB\) (đpcm)
Phân tích mẫu thức của cách phân thức ở vế trái thành nhân tử.
Từ đó đưa về dạng \(\frac{1}{{x\left( {x + 1} \right)}} = \frac{1}{x} - \frac{1}{{x + 1}}\).
Ta có: \(\frac{1}{{{x^2} + 9x + 20}} + \frac{1}{{{x^2} + 11x + 30}} + \frac{1}{{{x^2} + 13x + 42}} = \frac{1}{{18}}\)
Phân tích thành nhân tử:
* \({x^2} + 9x + 20\)\( = {x^2} + 4x + 5x + 20\)\( = \left( {{x^2} + 4x} \right) + \left( {5x + 20} \right)\)\( = x\left( {x + 4} \right) + 5\left( {x + 4} \right)\)\( = \left( {x + 4} \right)\left( {x + 5} \right)\)
* \({x^2} + 11x + 30\)\( = {x^2} + 5x + 6x + 30\)\( = \left( {{x^2} + 5x} \right) + \left( {6x + 30} \right)\)\( = x\left( {x + 5} \right) + 6\left( {x + 5} \right)\)\( = \left( {x + 5} \right)\left( {x + 6} \right)\)
* \({x^2} + 13x + 42\)\( = {x^2} + 6x + 7x + 42\)\( = \left( {{x^2} + 6x} \right) + \left( {7x + 42} \right)\)\( = x\left( {x + 6} \right) + 7\left( {x + 6} \right)\)\( = \left( {x + 6} \right)\left( {x + 7} \right)\)
suy ra phương trình trở thành \(\frac{1}{{(x + 4)(x + 5)}} + \frac{1}{{(x + 5)(x + 6)}} + \frac{1}{{(x + 6)(x + 7)}} = \frac{1}{{18}}\)
Điều kiện xác định: \(x \ne 4;{\mkern 1mu} x \ne 5;{\mkern 1mu} x \ne 6;{\mkern 1mu} x \ne 7\)
Ta có: \(\frac{1}{{(x + 4)(x + 5)}} + \frac{1}{{(x + 5)(x + 6)}} + \frac{1}{{(x + 6)(x + 7)}} = \frac{1}{{18}}\)
\(\begin{array}{l}\frac{1}{{x + 4}} - \frac{1}{{x + 5}} + \frac{1}{{x + 5}} - \frac{1}{{x + 6}} + \frac{1}{{x + 6}} - \frac{1}{{x + 7}} = \frac{1}{{18}}\\\frac{1}{{x + 4}} - \frac{1}{{x + 7}} = \frac{1}{{18}}\\\frac{{x + 7 - \left( {x + 4} \right)}}{{\left( {x + 4} \right)\left( {x + 7} \right)}} = \frac{1}{{18}}\\\frac{3}{{(x + 4)(x + 7)}} = \frac{1}{{18}}\end{array}\)
suy ra \((x + 4)(x + 7) = 54\)
\({x^2} + 7x + 4x + 28 = 54\)
\({x^2} + 11x - 26 = 0\)
\({x^2} + 13x - 2x - 26 = 0\)
\(x\left( {x + 13} \right) - 2\left( {x + 13} \right) = 0\)
\(\left( {x + 13} \right)\left( {x - 2} \right) = 0\)
Do đó \(x + 13 = 0\) hoặc \(x - 2 = 0\)
\(x = - 13\) (TM) \(x = 2\) (TM)
Vậy nghiệm của phương trình là \(x = - 13;x = 2\).
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần trắc nghiệm (3 điểm) Câu 1: Để giải phương trình $\frac{2x-3}{4}-\frac{1-x}{5}=1$, một bạn học sinh thực hiện như sau:
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn là
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn là
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
A. NỘI DUNG ÔN TẬP Đại số Phương trình bậc nhất và hàm số bậc nhất - Phương trình bậc nhất một ẩn - Giải bài toán bằng cách lập phương trình - Khái niệm hàm số và đồ thị của hàm số - Hàm số bậc nhất và đồ thị của hàm số bậc nhất - Hệ số góc của đường thẳng
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |










Danh sách bình luận