Đề thi học kì 2 Toán 8 Kết nối tri thức - Đề số 6
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Điều kiện xác định của phân thức \(\frac{{x - 1}}{{x - 2}}\) là:
-
A.
\(x \ne 1\).
-
B.
\(x \ne 2\).
-
C.
\(x \ne 1;x \ne 2\).
-
D.
\(x \in \mathbb{R}\).
Tích của phân thức \(\frac{{ - 2}}{{3{x^2}y}}\) với \( - 1\) là:
-
A.
\(\frac{2}{{3{x^2}y}}\).
-
B.
\(\frac{{ - 2}}{{6{x^2}y}}\).
-
C.
\(\frac{{ - 2}}{{3{x^2}y}}\).
-
D.
\(\frac{{ - 2}}{{3{x^2}{y^2}}}\).
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
-
A.
\(0x + 5 = 0\).
-
B.
\(2{x^2} - 3 = 0\).
-
C.
\(\frac{3}{x} - 2 = 0\).
-
D.
\(2x + 1 = 0\).
Phương trình \(3 - 2x = 0\) có nghiệm là:
-
A.
\(x = 3\).
-
B.
\(x = \frac{2}{3}\).
-
C.
\(x = \frac{3}{2}\).
-
D.
\(x = \frac{{ - 3}}{2}\).
Đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua
-
A.
gốc toạ độ \(O\left( {0;0} \right)\).
-
B.
điểm \(A\left( {1;0} \right)\).
-
C.
điểm \(B\left( {0;1} \right)\).
-
D.
điểm \(C\left( {1;1} \right)\).
Hệ số góc của đường thẳng \(y = x - 2\) là:
-
A.
-2.
-
B.
2.
-
C.
-1.
-
D.
1.
Một hộp có 30 quả bóng được đánh số từ 1 đến 30, đồng thời các quả bóng từ 1 đến 10 được sơn màu cam và các quả bóng còn lại được sơn màu xanh. Các quả bóng có kích cỡ và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Số kết quả thuận lợi của biến cố: “Quả bóng được lấy ra được sơn màu cam” là
-
A.
10.
-
B.
20.
-
C.
15.
-
D.
30.
Một hộp chứa 10 tấm thẻ cùng loại được đánh số thứ tự 4 đến 13. An lấy ra ngẫu nhiên một thẻ từ hộp. Xác suất để chọn ra thẻ ghi số chẵn là
-
A.
0,2.
-
B.
0,3.
-
C.
0,4.
-
D.
0,5.
Cho \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat M = \widehat D\). Điều kiện để $\Delta MNP\backsim \Delta DEF$ theo trường hợp góc – góc là
-
A.
\(\widehat N = \widehat F\).
-
B.
\(\widehat P = \widehat F\).
-
C.
\(\widehat M = \widehat E\).
-
D.
\(\widehat P = \widehat E\).
Cho $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng $k=1$ thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng là
-
A.
2.
-
B.
$\frac{1}{2}$.
-
C.
$1$.
-
D.
$3$.
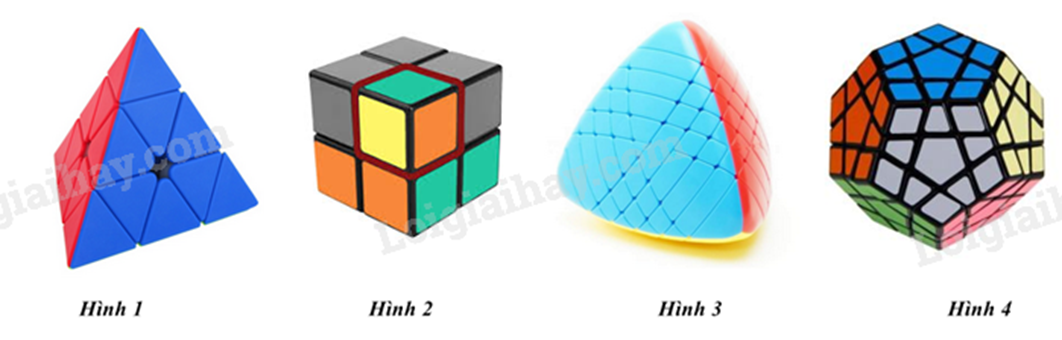
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Thể tích của hình chóp là
-
A.
tích nửa chu vi đáy và đường cao của hình chóp.
-
B.
tích nửa chu vi đáy và trung đoạn.
-
C.
một phần ba tích diện tích đáy và chiều cao.
-
D.
một phần ba tích diện tích đáy và trung đoạn.
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x + 1,\left( {{d_2}} \right):y = x + 1\).
a) Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau.
b) Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cùng đi qua điểm \(A\left( {1;0} \right)\).
c) Đường thẳng \(\left( {{d_3}} \right):y = 2x - 1\) đi qua \(E\left( { - 1;0} \right)\) và song song với \(\left( {{d_1}} \right)\).
d) Đường thẳng \(\left( {{d_4}} \right):y = 3x + 1\) đồng quy với \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và có hệ số góc là 3.
a) Bạn An đã gieo xúc xắc 50 lần.
b) Số kết quả thuận lợi của biến cố “Xuất hiện mặt 4 chấm” là 4.
c) Xác suất của biến cố “Xuất hiện mặt có số chấm chẵn” là 0,6.
d) Xác suất của biến cố xuất hiện mặt có số chấm không nhỏ hơn 3” là \(\frac{{14}}{{25}}\).
Cho đường thẳng \(\left( d \right):y = - 2x + 3\). Tìm \(m\) để đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( { - m; - 3} \right)\).
Đáp án:
Bạn An vào cửa hàng Lotteria và dự định mua một suất gà rán. Khi đọc menu, bạn An thấy cửa hàng đang có các món như sau: combo gà rán (ưu đãi) có giá 97 000 đồng, combo gà viên (ưu đãi) có giá 84 000 đồng, gà rán – 1 miếng có giá 35 000 đồng, gà rán – 2 miếng có giá 68 000 đồng, gà rán – 3 miếng có giá 101 000 đồng, cánh gà chiên – 3 miếng có giá 48 000 nghìn đồng. Bạn An cảm thấy món nào cũng ngon và dự định sẽ nhắm mắt chỉ tay chọn ngẫu nhiên một món. Tính xác suất “Món gà được bạn An chọn có giá dưới 70 000 đồng”. (Kết quả ghi dưới dạng số thập phân)
Đáp án:
Để đón một người khách, xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3 km đến điểm B thì rẽ vuông góc sang trái, chạy 3 km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1 km nữa thì gặp vị khách tại điểm D (như hình vẽ).
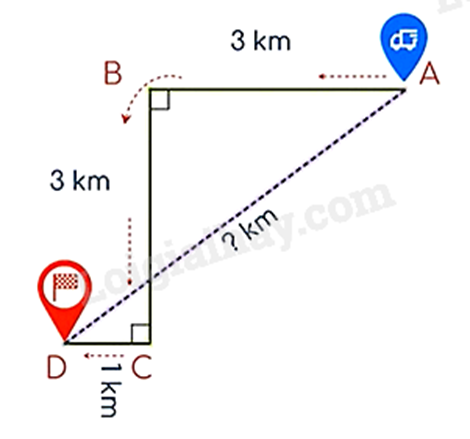
Hỏi lúc đầu khoảng cách từ chỗ người lái xe đến người khách là bao nhiêu kilômét?
Đáp án:
Nhà bạn An có một đèn trang trí có dạng hình chóp tam giác đều như hình vẽ bên. Các cạnh của hình chóp đều bằng nhau và bằng 20 cm. Bạn An dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu.
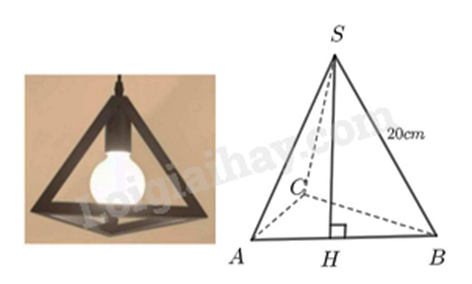
Tính diện tích giấy màu mà bạn An sử dụng (đơn vị: \(c{m^2}\), coi như mép dán không đáng kể). Cho biết \(\sqrt {300} = 17,32\). (Kết quả làm tròn đến hàng đơn vị)
Đáp án:
Lời giải và đáp án
Điều kiện xác định của phân thức \(\frac{{x - 1}}{{x - 2}}\) là:
-
A.
\(x \ne 1\).
-
B.
\(x \ne 2\).
-
C.
\(x \ne 1;x \ne 2\).
-
D.
\(x \in \mathbb{R}\).
Đáp án : B
Điều kiện xác định của phân thức \(\frac{A}{B}\) là \(B \ne 0\).
Điều kiện xác định của phân thức \(\frac{{x - 1}}{{x - 2}}\) là \(x - 2 \ne 0\) hay \(x \ne 2\).
Đáp án B
Tích của phân thức \(\frac{{ - 2}}{{3{x^2}y}}\) với \( - 1\) là:
-
A.
\(\frac{2}{{3{x^2}y}}\).
-
B.
\(\frac{{ - 2}}{{6{x^2}y}}\).
-
C.
\(\frac{{ - 2}}{{3{x^2}y}}\).
-
D.
\(\frac{{ - 2}}{{3{x^2}{y^2}}}\).
Đáp án : A
Muốn nhân hai phân thức với nhau, ta nhân tử thức với tử thức, mẫu thức với mẫu thức sau đó rút gọn kết quả (nếu cần).
Ta có: \(\frac{{ - 2}}{{3{x^2}y}}.\left( { - 1} \right) = \frac{2}{{3{x^2}y}}\).
Đáp án A
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
-
A.
\(0x + 5 = 0\).
-
B.
\(2{x^2} - 3 = 0\).
-
C.
\(\frac{3}{x} - 2 = 0\).
-
D.
\(2x + 1 = 0\).
Đáp án : D
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\left( {a \ne 0} \right)\).
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\left( {a \ne 0} \right)\).
Do đó \(2x + 1 = 0\) là phương trình bậc nhất một ẩn.
Đáp án D
Phương trình \(3 - 2x = 0\) có nghiệm là:
-
A.
\(x = 3\).
-
B.
\(x = \frac{2}{3}\).
-
C.
\(x = \frac{3}{2}\).
-
D.
\(x = \frac{{ - 3}}{2}\).
Đáp án : C
Giải phương trình bậc nhất một ẩn:
\(\begin{array}{l}ax + b = 0\\ax = - b\\x = - \frac{b}{a}\end{array}\)
Ta có:
\(\begin{array}{l}3 - 2x = 0\\ - 2x = - 3\\x = \frac{3}{2}\end{array}\)
Vậy \(x = \frac{3}{2}\)
Đáp án C
Đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua
-
A.
gốc toạ độ \(O\left( {0;0} \right)\).
-
B.
điểm \(A\left( {1;0} \right)\).
-
C.
điểm \(B\left( {0;1} \right)\).
-
D.
điểm \(C\left( {1;1} \right)\).
Đáp án : A
Dựa vào kiến thức về đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\).
Đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua gốc toạ độ \(O\left( {0;0} \right)\).
Đáp án A
Hệ số góc của đường thẳng \(y = x - 2\) là:
-
A.
-2.
-
B.
2.
-
C.
-1.
-
D.
1.
Đáp án : D
Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là a.
Hệ số góc của đường thẳng \(y = x - 2\) là \(a = 1\).
Đáp án D
Một hộp có 30 quả bóng được đánh số từ 1 đến 30, đồng thời các quả bóng từ 1 đến 10 được sơn màu cam và các quả bóng còn lại được sơn màu xanh. Các quả bóng có kích cỡ và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Số kết quả thuận lợi của biến cố: “Quả bóng được lấy ra được sơn màu cam” là
-
A.
10.
-
B.
20.
-
C.
15.
-
D.
30.
Đáp án : A
Xác định các số thoả mãn quả bóng được sơn màu cam.
Số kết quả thuận lợi của biến cố “Quả bóng được lấy ra có màu cam” là 10, đó là các quả bóng từ 1 đến 10.
Đáp án A
Một hộp chứa 10 tấm thẻ cùng loại được đánh số thứ tự 4 đến 13. An lấy ra ngẫu nhiên một thẻ từ hộp. Xác suất để chọn ra thẻ ghi số chẵn là
-
A.
0,2.
-
B.
0,3.
-
C.
0,4.
-
D.
0,5.
Đáp án : D
Xác định các thẻ ghi số chẵn, ta được số các kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể (tổng số thẻ).
Các kết quả thuận lợi cho biến cố “lấy được thẻ ghi số chẵn” là: 4; 6; 8; 10; 12.
Do đó có 5 kết quả thuận lợi.
Có 10 kết quả có thể khi lấy ngẫu nhiên một thẻ từ hộp.
Xác suất để chọn được thẻ ghi số chẵn là: \(\frac{5}{{10}} = 0,5\).
Đáp án D
Cho \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat M = \widehat D\). Điều kiện để $\Delta MNP\backsim \Delta DEF$ theo trường hợp góc – góc là
-
A.
\(\widehat N = \widehat F\).
-
B.
\(\widehat P = \widehat F\).
-
C.
\(\widehat M = \widehat E\).
-
D.
\(\widehat P = \widehat E\).
Đáp án : B
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu chúng có hai cặp góc bằng nhau.
Để $\Delta MNP\backsim \Delta DEF\left( g.g \right)$ có \(\widehat M = \widehat D\) thì ta cần thêm \(\widehat P = \widehat F\) hoặc \(\widehat N = \widehat E\) nên ta chọn B.
Đáp án B
Cho $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng $k=1$ thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng là
-
A.
2.
-
B.
$\frac{1}{2}$.
-
C.
$1$.
-
D.
$3$.
Đáp án : C
Nếu $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng $k$ thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng $\frac{1}{k}$.
Để $\Delta MNP\backsim \Delta A'B'C'$ theo tỉ số đồng dạng $k=1$ thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng $k'=\frac{1}{k}=\frac{1}{1}=1$.
Đáp án C
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : A
Hình chóp tam giác đều là hình có 3 mặt bên và 1 mặt đáy đều là các tam giác đều.
Hình có dạng hình chóp tam giác đều là Hình 1.
Đáp án A
Thể tích của hình chóp là
-
A.
tích nửa chu vi đáy và đường cao của hình chóp.
-
B.
tích nửa chu vi đáy và trung đoạn.
-
C.
một phần ba tích diện tích đáy và chiều cao.
-
D.
một phần ba tích diện tích đáy và trung đoạn.
Đáp án : C
Dựa vào kiến thức về thể tích của hình chóp.
Thể tích của hình chóp là một phần ba tích diện tích đáy và chiều cao.
Đáp án C
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x + 1,\left( {{d_2}} \right):y = x + 1\).
a) Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau.
b) Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cùng đi qua điểm \(A\left( {1;0} \right)\).
c) Đường thẳng \(\left( {{d_3}} \right):y = 2x - 1\) đi qua \(E\left( { - 1;0} \right)\) và song song với \(\left( {{d_1}} \right)\).
d) Đường thẳng \(\left( {{d_4}} \right):y = 3x + 1\) đồng quy với \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và có hệ số góc là 3.
a) Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau.
b) Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cùng đi qua điểm \(A\left( {1;0} \right)\).
c) Đường thẳng \(\left( {{d_3}} \right):y = 2x - 1\) đi qua \(E\left( { - 1;0} \right)\) và song song với \(\left( {{d_1}} \right)\).
d) Đường thẳng \(\left( {{d_4}} \right):y = 3x + 1\) đồng quy với \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và có hệ số góc là 3.
a) Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau nếu \(a \ne a'\).
b) Cách 1. Vì hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau nên điểm duy nhất mà hai đường thẳng cùng đi qua là giao điểm của hai đường thẳng đó.
Xét phương trình hoành độ giao điểm hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) để tìm hoành độ giao điểm: \(ax + b = a'x + b'\).
Từ đó tính tung độ giao điểm.
Cách 2. Thay toạ độ điểm \(A\left( {1;0} \right)\) vào \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) để xem \(A\left( {1;0} \right)\) có thuộc hai đường thẳng hay không.
c) Gọi đường thẳng \(\left( {{d_3}} \right)\) có dạng \(\left( {{d_3}} \right):y = ax + b\).
Vì \(\left( {{d_3}} \right)//\left( {{d_1}} \right)\) nên ta tìm được hệ số a (hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song khi \(a = a',b \ne b'\).
Vì \(\left( {{d_3}} \right)\) đi qua \(E\left( { - 1;0} \right)\) nên ta thay \(E\left( { - 1;0} \right)\) vào \(\left( {{d_3}} \right)\) để tìm b.
d) Gọi đường thẳng \(\left( {{d_4}} \right)\) có dạng \(y = ax + b\).
Vì đường thẳng \(\left( {{d_4}} \right)\) có hệ số góc là 3 ta tìm được a.
Mà đường thẳng \(\left( {{d_4}} \right)\) đồng quy với \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) nên đường thẳng \(\left( {{d_4}} \right)\) cũng đi qua giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
Do đó thay toạ độ giao điểm vào đường thẳng \(\left( {{d_4}} \right)\) để tìm b.
a) Đúng
Ta có: \(2 \ne 1\) nên hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau.
b) Sai
Cách 1. Vì hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau nên điểm duy nhất mà hai đường thẳng cùng đi qua là giao điểm của hai đường thẳng đó.
Xét phương trình hoành độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\), ta có:
\(\begin{array}{l}2x + 1 = x + 1\\2x - x = 1 - 1\\x = 0\end{array}\)
Khi đó \(y = 2.0 + 1 = 1\) nên giao điểm của hai đường thẳng là điểm \(A'\left( {0;1} \right) \ne A\left( {1;0} \right)\).
Do đó khẳng định b sai.
Cách 2. Thay toạ độ điểm \(A\left( {1;0} \right)\) vào \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
* Thay toạ độ điểm \(A\left( {1;0} \right)\) vào \(\left( {{d_1}} \right):y = 2x + 1\):
Với \(x = 1\) thì \(y = 2.1 + 1 = 3 \ne 0\) nên điểm \(A\left( {1;0} \right)\) không thuộc đường thẳng \(\left( {{d_1}} \right):y = 2x + 1\).
* Thay toạ độ điểm \(A\left( {1;0} \right)\) vào \(\left( {{d_2}} \right):y = x + 1\):
Với \(x = 1\) thì \(y = 1 + 1 = 2 \ne 0\) nên điểm \(A\left( {1;0} \right)\) không thuộc đường thẳng \(\left( {{d_2}} \right):y = x + 1\).
Do đó hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) không đi qua điểm \(A\left( {1;0} \right)\).
c) Sai
Gọi đường thẳng \(\left( {{d_3}} \right)\) có dạng \(\left( {{d_3}} \right):y = ax + b\).
Vì \(\left( {{d_3}} \right)//\left( {{d_1}} \right)\) nên \(a = 2,b \ne 1\). Do đó ta có \(\left( {{d_3}} \right):y = 2x + b\).
Thay \(E\left( { - 1;0} \right)\) vào \(\left( {{d_3}} \right)\), ta được:
\(\begin{array}{l}2.\left( { - 1} \right) + b = 0\\ - 2 + b = 0\\b = 0 - \left( { - 2} \right)\\b = 2\left( {TM} \right)\end{array}\)
Vậy đường thẳng \(\left( {{d_3}} \right):y = 2x + 2\).
d) Đúng
Gọi đường thẳng \(\left( {{d_4}} \right)\) có dạng \(y = ax + b\).
Vì đường thẳng \(\left( {{d_4}} \right)\) có hệ số góc là 3 nên ta có: \(\left( {{d_4}} \right):y = 3x + b\).
Mà đường thẳng \(\left( {{d_4}} \right)\) đồng quy với \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) nên đường thẳng \(\left( {{d_4}} \right)\) cũng đi qua giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
Do đó \(A'\left( {0;1} \right)\) thuộc đường thẳng \(\left( {{d_4}} \right)\). Thay \(A'\left( {0;1} \right)\) vào \(\left( {{d_4}} \right)\), ta được:
\(\begin{array}{l}3.0 + b = 1\\b = 1\end{array}\)
Vậy đường thẳng \(\left( {{d_4}} \right):y = 3x + 1\).
Đáp án: ĐSSĐ
a) Bạn An đã gieo xúc xắc 50 lần.
b) Số kết quả thuận lợi của biến cố “Xuất hiện mặt 4 chấm” là 4.
c) Xác suất của biến cố “Xuất hiện mặt có số chấm chẵn” là 0,6.
d) Xác suất của biến cố xuất hiện mặt có số chấm không nhỏ hơn 3” là \(\frac{{14}}{{25}}\).
a) Bạn An đã gieo xúc xắc 50 lần.
b) Số kết quả thuận lợi của biến cố “Xuất hiện mặt 4 chấm” là 4.
c) Xác suất của biến cố “Xuất hiện mặt có số chấm chẵn” là 0,6.
d) Xác suất của biến cố xuất hiện mặt có số chấm không nhỏ hơn 3” là \(\frac{{14}}{{25}}\).
a) Dựa vào bảng thống kê số lần để tính tổng số lần gieo.
b) Quan sát bảng xác định số lần xuất hiện mặt 4 chấm.
c) Xác định số kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
d) Xác định số kết quả thuận lợi cho biến cố (số chấm không nhỏ hơn 3 ta tính các kết quả số chấm 3, 4, 5, 6).
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
a) Đúng
Bạn An đã gieo tổng số lần là:
10 + 8 + 6 + 12 + 4 + 10 = 50 (lần)
b) Sai
Quan sát bảng, ta thấy số kết quả thuận lợi cho biến cố “Xuất hiện mặt 4 chấm” là 12.
c) Đúng
Kết quả thuận lợi cho biến cố “Xuất hiện mặt có số chấm chẵn” là:
12 + 8 + 10 = 30.
Xác suất của biến cố “Xuất hiện số mặt có 30 số chấm chẵn” là: \(\frac{{30}}{{50}} = 0,6\).
d) Sai
Kết quả thuận lợi của biến cố “Xuất hiện mặt có số chấm không nhỏ hơn 3" là:
6 + 12 + 4 + 10 = 32
Do đó xác suất của biến cố đó là: \(\frac{{36}}{{50}} = \frac{{16}}{{25}}\).
Đáp án: ĐSĐS
Cho đường thẳng \(\left( d \right):y = - 2x + 3\). Tìm \(m\) để đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( { - m; - 3} \right)\).
Đáp án:
Đáp án:
Thay toạ độ điểm \(A\left( { - m; - 3} \right)\) vào \(\left( d \right):y = - 2x + 3\) để tìm m
Thay toạ độ điểm \(A\left( { - m; - 3} \right)\) vào \(\left( d \right):y = - 2x + 3\), ta được:
\(\begin{array}{l} - 2\left( { - m} \right) + 3 = - 3\\2m = - 3 - 3\\2m = - 6\\m = \left( { - 6} \right):2\\m = - 3\end{array}\)
Đáp án: -3
Bạn An vào cửa hàng Lotteria và dự định mua một suất gà rán. Khi đọc menu, bạn An thấy cửa hàng đang có các món như sau: combo gà rán (ưu đãi) có giá 97 000 đồng, combo gà viên (ưu đãi) có giá 84 000 đồng, gà rán – 1 miếng có giá 35 000 đồng, gà rán – 2 miếng có giá 68 000 đồng, gà rán – 3 miếng có giá 101 000 đồng, cánh gà chiên – 3 miếng có giá 48 000 nghìn đồng. Bạn An cảm thấy món nào cũng ngon và dự định sẽ nhắm mắt chỉ tay chọn ngẫu nhiên một món. Tính xác suất “Món gà được bạn An chọn có giá dưới 70 000 đồng”. (Kết quả ghi dưới dạng số thập phân)
Đáp án:
Đáp án:
Xác định tập hợp các kết quả có thể xảy ra đối với món gà mà bạn An chọn, từ đó suy ra số kết quả có thể xảy ra.
Xác định các kết quả thuận lợi cho biến cố “Món gà được bạn An chọn có giá dưới 70 000 đồng”, suy ra số kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
Tập hợp các kết quả có thể xảy ra đối với món gà mà bạn An chọn là:
A = {combo gà rán; combo gà viên; gà rán - 1 miếng; gà rán – 2 miếng; gà rán – 3 miếng; cánh gà chiên – 3 miếng}.
Vậy có 6 kết quả có thể xảy ra.
Kết quả thuận lợi cho biến cố “Món gà được bạn An chọn có giá dưới 70 000 đồng” là: gà rán – miếng giá 35 000 đồng; gà rán – 2 miếng giá 68 000 và cánh gà chiên – 3 miếng giá 48 000 đồng.
Do đó, có 3 kết quả thuận lợi cho biến cố.
Vậy xác suất của biến cố “Món gà được bạn An chọn có giá dưới 70 000 đồng” là: \(\frac{3}{6} = \frac{1}{2} = 0,5\).
Đáp án: 0,5
Để đón một người khách, xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3 km đến điểm B thì rẽ vuông góc sang trái, chạy 3 km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1 km nữa thì gặp vị khách tại điểm D (như hình vẽ).

Hỏi lúc đầu khoảng cách từ chỗ người lái xe đến người khách là bao nhiêu kilômét?
Đáp án:
Đáp án:
Gọi điểm M sao cho ABCM là hình vuông.
Khi đó ta tính độ dài đoạn thẳng DM.
Áp dụng định lí Pythagore vào tam giác \(\Delta AMD\) để tính AD là khoảng cách từ chỗ người lái xe đến người khách.
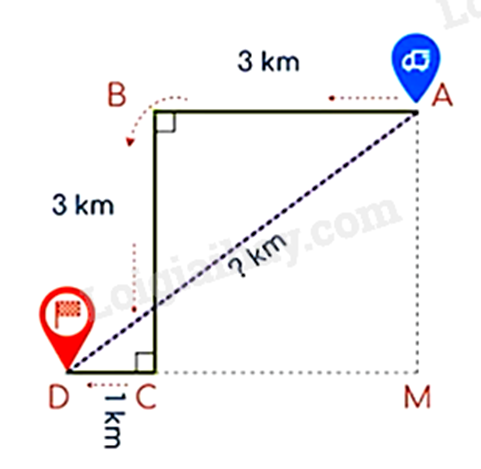
Gọi điểm M sao cho ABCM là hình vuông.
Ta có: DM = DC + CM = DC + BA = 1 + 3 = 4 (km)
Áp dụng định lí Pythagore vào tam giác \(\Delta AMD\), ta có:
\(A{D^2} = D{M^2} + A{M^2}\)
\(\begin{array}{l}A{D^2} = {4^2} + {3^2}\\A{D^2} = 25\end{array}\)
nên \(AD = 5\left( {km} \right)\)
Vậy khoảng cách lúc đầu từ chỗ người lái xe đến người khách là 5 km.
Đáp án: 5
Nhà bạn An có một đèn trang trí có dạng hình chóp tam giác đều như hình vẽ bên. Các cạnh của hình chóp đều bằng nhau và bằng 20 cm. Bạn An dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu.

Tính diện tích giấy màu mà bạn An sử dụng (đơn vị: \(c{m^2}\), coi như mép dán không đáng kể). Cho biết \(\sqrt {300} = 17,32\). (Kết quả làm tròn đến hàng đơn vị)
Đáp án:
Đáp án:
Các mặt bên và mặt đáy của hình chóp S.ABC là những tam giác đều cạnh 20 cm.
Chứng minh SH là đường trung tuyến của tam giác SAB suy ra độ dài đoạn AH.
Áp dụng định lí Pythagore vào tam giác đều SHB vuông tại H để tính SH.
Tính nửa chu vi đáy.
Tính diện tích xung quanh của hình chóp tam giác đều S.ABC: \({S_{xq}} = P.d\).
Các mặt bên và mặt đáy của hình chóp S.ABC là những tam giác đều cạnh 20 cm.
Xét tam giác đều SAB có đường cao SH đồng thời là đường trung tuyến, ta có:
\(AH = BH = \frac{{AB}}{2} = 10\left( {cm} \right)\)
Áp dụng định lí Pythagore vào tam giác đều SHB vuông tại H, ta có:
\(S{B^2} = S{H^2} + B{H^2}\)
\({20^2} = S{H^2} + {10^2}\)
Do đó: \(S{H^2} = {20^2} - {10^2} = 400 - 100 = 300\)
Suy ra \(SH = \sqrt {300} = 17,32\left( {cm} \right)\)
Nửa chu vi đáy là:
\(P = \frac{1}{2}\left( {20 + 20 + 20} \right) = 30\left( {cm} \right)\)
Diện tích xung quanh của hình chóp tam giác đều S.ABC là: \({S_{xq}} = P.d = P.SH = 30.17,32 = 519,6 \approx 520\left( {c{m^2}} \right)\)
Đáp án: 520
Gọi nồng độ muối trong dung dịch I là \(x\left( \% \right)\) với \(x > 20\).
Biểu diễn lượng muối có trong dung dịch I, nồng độ muối trong dung dịch II, lượng muối trong dung dịch II, khối lượng muối trong dung dịch sau khi trộn hai dung dịch theo \(x\).
Tính khối lượng dung dịch muối sau khi trộn hai dung dịch, từ đó lập phương trình biểu diễn nồng độ muối sai khi trộn hai dung dịch I và II.
Giải phương trình và kiểm tra điều kiện.
Từ đó tính nồng độ muối trong dung dịch II.
Gọi nồng độ muối trong dung dịch I là \(x\left( \% \right)\) với \(x > 20\).
Khi đó lượng muối có trong dung dịch I là:
\(200.\frac{x}{{100}} = 2x\left( g \right)\).
Do nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20% nên nồng độ muối trong dung dịch II là: \(x - 20\left( \% \right)\)
Khi đó lượng muối trong dung dịch II là: \(300.\frac{{x - 20}}{{100}} = 3\left( {x - 20} \right)\left( g \right)\)
Khối lượng muối trong dung dịch sau khi trộn hai dung dịch là: \(2x + 3\left( {x - 20} \right)\left( g \right)\)
Khối lượng dung dịch muối sau khi trộn hai dung dịch là: \(200 + 300 = 500\left( g \right)\)
Do sau khi trộn hai dung dịch I và II thì được một dung dịch có nồng độ muối là 33% nên ta có phương trình:
\(\frac{{2x + 3\left( {x - 20} \right)}}{{500}}.100\% = 33\% \)
Giải phương trình, ta được:
\(\frac{{2x + 3\left( {x - 20} \right)}}{{500}}.100\% = 33\% \).
\(\frac{{2x + 3\left( {x - 20} \right)}}{5} = 33\)
\(\begin{array}{l}2x + 3x - 60 = 33.5\\5x - 60 = 165\\5x = 165 + 60\\5x = 225\\x = 225:5\\x = 45\left( {TM} \right)\end{array}\)
Suy ra nồng độ muối trong dung dịch II là: 45 – 20 = 25(%).
Vậy nồng độ muối của dung dịch I và II lần lượt là 45% và 25%.
a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ \) (gt)
\(\widehat {ACB}\) chung
nên $\Delta ABC\backsim \Delta HAC$ (g.g)
b) Chứng minh $\Delta CHI\backsim \Delta CKB$ (g.g) suy ra $CH\cdot CB=CI\cdot CK$
c) Chứng minh \(I\) là trực tâm của \(\Delta BDC\), suy ra \(BI \bot DC\).
Gọi \(M\) là giao điểm của BI và DC, khi đó \(BM \bot CD\) nên \(\widehat {BMC} = 90^\circ \)
Chứng minh $\Delta CMI\backsim \Delta CDK$ (g.g) suy ra \(CD \cdot CM = CI \cdot CK\)
Kết hợp với phần b) ta được \(CH \cdot CB = CD \cdot CM\left( { = CI \cdot CK} \right)\) (1)
Chứng minh $\Delta MDB \backsim \Delta KDC$ (g.g) suy ra \(DK \cdot DB = DM \cdot DC\) (2)
Cộng (1) và (2) để được điều phải chứng minh.
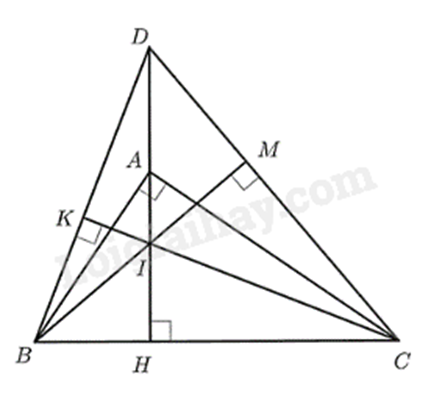
a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ \) (gt)
\(\widehat {ACB}\) chung
nên $\Delta ABC\backsim \Delta HAC$ (g.g)
b) Xét \(\Delta CHI\) và \(\Delta CKB\) có:
\(\widehat {CHI} = \widehat {CKB} = 90^\circ \) (gt)
\(\,\widehat {HCI}\) chung
nên $\Delta CHI\backsim \Delta CKB$ (g.g)
suy ra \(\frac{{CH}}{{CK}} = \frac{{CI}}{{CB}}\)
do đó \(CH \cdot CB = CI \cdot CK\)
c) Vì \(DH \bot BC\) (do \(HA \bot BC\), D thuộc tia HA) nên DH là đường cao của \(\Delta BDC\).
Vì \(CK \bot BD\) (do \(CI \bot BK\)) nên CK là đường cao của \(\Delta BDC\).
Mà DH cắt CK tại I nên \(I\) là trực tâm của \(\Delta BDC\), suy ra \(BI \bot DC\).
Gọi \(M\) là giao điểm của BI và DC, khi đó \(BM \bot CD\) nên \(\widehat {BMC} = 90^\circ \)
Xét \(\Delta CMI\) và \(\Delta CDK\), ta có:
\(\widehat {CMI} = \widehat {CKD} = 90^\circ \) (cmt)
\(\widehat {DCK}\) chung
nên $\Delta CMI\backsim \Delta CKD$ (g.g)
suy ra \(\frac{{CM}}{{CK}} = \frac{{CI}}{{CD}}\), do đó \(CD \cdot CM = CI \cdot CK\)
Mà từ phần b) ta có: \(CH \cdot CB = CI \cdot CK\)
Suy ra \(CH \cdot CB = CD \cdot CM\left( { = CI \cdot CK} \right)\) (1)
Xét \(\Delta MDB\) và \(\Delta KDC\), ta có:
\(\widehat {DMB} = \widehat {DKC} = 90^\circ \) (cmt)
\(\widehat {BDC}\) chung
nên $\Delta MDB \backsim \Delta KDC$ (g.g)
suy ra \(\frac{{DB}}{{DC}} = \frac{{DM}}{{DK}}\), do đó \(DK \cdot DB = DM \cdot DC\) (2)
Từ (1) và (2) ta có:
\(CH \cdot CB + DK \cdot DB = CD \cdot CM + DM \cdot DC\)\( = DC \cdot (MD + MC) = D{C^2}\)
Sử dụng kiến thức về hiệu hai bình phương để biến đổi các mẫu thức, từ đó rút gọn biểu thức.
Ta có: \(A = \frac{{{1^2}}}{{{2^2} - 1}}.\frac{{{3^2}}}{{{4^2} - 1}}.\frac{{{5^2}}}{{{6^2} - 1}}.....\frac{{{n^2}}}{{{{\left( {n + 1} \right)}^2} - 1}}\)
\(A = \frac{{{1^2}}}{{\left( {2 - 1} \right)\left( {2 + 1} \right)}}.\frac{{{3^2}}}{{\left( {4 - 1} \right)\left( {4 + 1} \right)}}.\frac{{{5^2}}}{{\left( {6 - 1} \right)\left( {6 + 1} \right)}}.....\frac{{{n^2}}}{{\left( {n + 1 - 1} \right)\left( {n + 1 + 1} \right)}}\)
\(A = \frac{{{1^2}}}{{1.3}}.\frac{{{3^2}}}{{3.5}}.\frac{{{5^2}}}{{5.7}}.....\frac{{{n^2}}}{{n\left( {n + 2} \right)}}\)
\(A = \frac{1}{3}.\frac{3}{5}.\frac{5}{7}.....\frac{n}{{n + 2}}\)
\(A = \frac{1}{{n + 2}}\)
Vậy \(A = \frac{1}{{n + 2}}\).
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần trắc nghiệm (3 điểm) Câu 1: Để giải phương trình $\frac{2x-3}{4}-\frac{1-x}{5}=1$, một bạn học sinh thực hiện như sau:
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn là
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn là
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
A. NỘI DUNG ÔN TẬP Đại số Phương trình bậc nhất và hàm số bậc nhất - Phương trình bậc nhất một ẩn - Giải bài toán bằng cách lập phương trình - Khái niệm hàm số và đồ thị của hàm số - Hàm số bậc nhất và đồ thị của hàm số bậc nhất - Hệ số góc của đường thẳng
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |











Danh sách bình luận