Đề thi học kì 2 Toán 8 - Đề số 4 - Kết nối tri thức
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn là
Đề bài
Trong các phương trình sau, phương trình bậc nhất một ẩn là
-
A.
\({x^2} - 1 = 0\).
-
B.
\(3x + 2 = 0\).
-
C.
\(\frac{1}{x} - 3x = 0\).
-
D.
\(\frac{2}{{x - 3}} = 0\).
Nghiệm của phương trình \(4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\) là?
-
A.
\(x = 2\).
-
B.
\(x = \frac{1}{2}\).
-
C.
\(x = 1\).
-
D.
\(x = - 1\).
Trong các hàm số sau, hàm số nào là hàm số bậc nhất một ẩn?
-
A.
\(y = 0x + 3\).
-
B.
\(y = x - 2\).
-
C.
\(y = {x^2}\).
-
D.
\(y = - 5\).
Giá trị của m để đường thẳng \(y = \left( {m - 3} \right)x - 1 + m\) và đường thẳng \(y = x + 1\) song song với nhau là:
-
A.
\(m = 2\).
-
B.
\(m = 3\).
-
C.
\(m = 4\).
-
D.
\(m = 5\).
Bạn An tung một đồng xu cân đối và đồng chất 20 lần, có 9 lần mặt ngửa, 11 lần mặt sấp. Xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là:
-
A.
\(\frac{9}{{11}}\).
-
B.
\(\frac{{11}}{9}\).
-
C.
\(\frac{9}{{20}}\).
-
D.
\(\frac{{11}}{{20}}\).
Một hộp có 10 tấm thẻ cùng loại được đánh số từ 5 đến 14. Bạn An lấy ra ngẫu nhiên 1 thẻ từ hộp. Xác suất của biến cố “Chọn ra thẻ ghi số chia hết cho 5” là bao nhiêu phần trăm?
-
A.
20%.
-
B.
30%.
-
C.
40%.
-
D.
50%.
Trong các miếng bìa sau, miếng bìa nào khi gấp và dán lại thì được một hình chóp tứ giác đều?
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
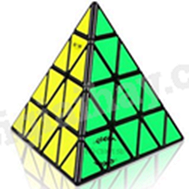
Tính thể tích khối rubik có dạng hình chóp tam giác đều (hình bên). Biết khối rubik này có bốn mặt là các tam giác đều bằng nhau cạnh 5,2cm và chiều cao của tam giác là 4,5cm; chiều cao của khối rubik bằng 4,2cm.
-
A.
\(49,14c{m^3}\).
-
B.
\(32,76c{m^3}\).
-
C.
\(16,38c{m^3}\).
-
D.
\(98,28c{m^3}\).
-
A.
$\Delta DEF\backsim \Delta HIK$.
-
B.
$\Delta DEF\backsim \Delta MNP$.
-
C.
$\Delta HIK\backsim \Delta MNP$.
-
D.
Cả 3 tam giác đồng dạng.
-
A.
6,4.
-
B.
3,6.
-
C.
17,7.
-
D.
5,6.
Trong các hình sau, cặp hình nào không phải luôn đồng dạng?
-
A.
Tam giác cân.
-
B.
Hình tròn.
-
C.
Tam giác đều.
-
D.
Hình vuông.
-
A.
\(k = \frac{1}{2}\).
-
B.
\(k = 1\).
-
C.
\(k = 2\).
-
D.
\(k = 4\).
Lời giải và đáp án
Trong các phương trình sau, phương trình bậc nhất một ẩn là
-
A.
\({x^2} - 1 = 0\).
-
B.
\(3x + 2 = 0\).
-
C.
\(\frac{1}{x} - 3x = 0\).
-
D.
\(\frac{2}{{x - 3}} = 0\).
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình bậc nhất một ẩn là phương trình \(3x + 2 = 0\).
Đáp án B.
Nghiệm của phương trình \(4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\) là?
-
A.
\(x = 2\).
-
B.
\(x = \frac{1}{2}\).
-
C.
\(x = 1\).
-
D.
\(x = - 1\).
Đáp án : B
Đưa phương trình về dạng \(ax + b = 0\) để giải.
\(\begin{array}{l}4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\\4x - 4 - x + 2 = - x\\3x - 2 = - x\\3x + x = 2\\4x = 2\\x = \frac{1}{2}\end{array}\)
Vậy \(x = \frac{1}{2}\)
Đáp án B.
Trong các hàm số sau, hàm số nào là hàm số bậc nhất một ẩn?
-
A.
\(y = 0x + 3\).
-
B.
\(y = x - 2\).
-
C.
\(y = {x^2}\).
-
D.
\(y = - 5\).
Đáp án : B
Hàm số bậc nhất một ẩn có dạng \(y = ax + b\left( {a \ne 0} \right)\).
Hàm số bậc nhất một ẩn là \(y = x - 2\).
Đáp án B.
Giá trị của m để đường thẳng \(y = \left( {m - 3} \right)x - 1 + m\) và đường thẳng \(y = x + 1\) song song với nhau là:
-
A.
\(m = 2\).
-
B.
\(m = 3\).
-
C.
\(m = 4\).
-
D.
\(m = 5\).
Đáp án : C
Hai hàm số \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau nếu \(a = a';b \ne b'\).
Đường thẳng \(y = \left( {m - 3} \right)x - 1 + m\) và đường thẳng \(y = x + 1\) song song với nhau nếu:
\(\begin{array}{l}\left\{ \begin{array}{l}m - 3 = 1\\ - 1 + m \ne 1\end{array} \right.\\\left\{ \begin{array}{l}m = 4\\m \ne 2\end{array} \right.\end{array}\)
Vậy \(m = 4\) thì đường thẳng \(y = \left( {m - 3} \right)x - 1 + m\) và đường thẳng \(y = x + 1\) song song với nhau.
Đáp án C.
Bạn An tung một đồng xu cân đối và đồng chất 20 lần, có 9 lần mặt ngửa, 11 lần mặt sấp. Xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là:
-
A.
\(\frac{9}{{11}}\).
-
B.
\(\frac{{11}}{9}\).
-
C.
\(\frac{9}{{20}}\).
-
D.
\(\frac{{11}}{{20}}\).
Đáp án : D
Xác định số lần mặt sấp xuất hiện.
Xác suất thực nghiệm của biến cố bằng tỉ số giữa số lần mặt sấp xuất hiện với tổng số lần tung.
Mặt sấp xuất hiện 11 lần nên xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là \(\frac{{11}}{{20}}\).
Đáp án D.
Một hộp có 10 tấm thẻ cùng loại được đánh số từ 5 đến 14. Bạn An lấy ra ngẫu nhiên 1 thẻ từ hộp. Xác suất của biến cố “Chọn ra thẻ ghi số chia hết cho 5” là bao nhiêu phần trăm?
-
A.
20%.
-
B.
30%.
-
C.
40%.
-
D.
50%.
Đáp án : A
Xác định kết quả thuận lợi cho biến cố.
Tính xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả.
Các thẻ ghi số chia hết cho 5 là: 5; 10.
Có 2 kết quả thuận lợi cho biến cố “Chọn ra thẻ ghi số chia hết cho 5”.
Xác suất của biến cố “Chọn ra thẻ ghi số chia hết cho 5” là:
\(\frac{2}{{10}} = 0,2 = 20\% \)
Đáp án A.
Trong các miếng bìa sau, miếng bìa nào khi gấp và dán lại thì được một hình chóp tứ giác đều?
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : A
Dựa vào đặc điểm của hình chóp tứ giác đều.
Miếng bìa gấp và dán lại được một tứ giác đều là hình 1 vì hình chóp tứ giác đều có 4 mặt bên là các tam giác vuông và 1 mặt đáy là hình vuông.
Đáp án A.
Tính thể tích khối rubik có dạng hình chóp tam giác đều (hình bên). Biết khối rubik này có bốn mặt là các tam giác đều bằng nhau cạnh 5,2cm và chiều cao của tam giác là 4,5cm; chiều cao của khối rubik bằng 4,2cm.
-
A.
\(49,14c{m^3}\).
-
B.
\(32,76c{m^3}\).
-
C.
\(16,38c{m^3}\).
-
D.
\(98,28c{m^3}\).
Đáp án : C
Dựa vào công thức tính thể tích hình chóp tam giác đều.
Thể tích của khối rubik là:
\(V = \frac{1}{3}.4,2.\left( {\frac{1}{2}.4,5.5,2} \right) = 16,38\left( {{m^3}} \right)\).
Đáp án C.
-
A.
$\Delta DEF\backsim \Delta HIK$.
-
B.
$\Delta DEF\backsim \Delta MNP$.
-
C.
$\Delta HIK\backsim \Delta MNP$.
-
D.
Cả 3 tam giác đồng dạng.
Đáp án : B
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
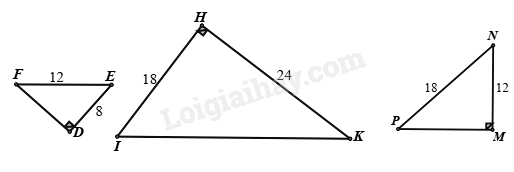
Xét \(\Delta DEF\) và \(\Delta MNP\) có:
\(\begin{array}{l}\widehat D = \widehat M = {90^0}\\\frac{{DE}}{{MN}} = \frac{{EF}}{{NP}}\left( {\frac{8}{{12}} = \frac{{12}}{{18}}\left( { = \frac{2}{3}} \right)} \right)\end{array}\)
nên $\Delta DEF\backsim \Delta MNP$(cạnh huyền – cạnh góc vuông)
Áp dụng định lí Pythagore vào tam giác HIK có:
\(KI = \sqrt {{{18}^2} + {{24}^2}} = 30\)
Vì \(\frac{8}{{12}} = \frac{2}{3} \ne \frac{{18}}{{30}} = \frac{3}{5}\) nên \(\Delta DEF\) không đồng dạng với \(\Delta HIK\).
Điều này dẫn đến \(\Delta MNP\) không đồng dạng với \(\Delta HIK\)(vì $\Delta DEF\backsim \Delta MNP$)
Đáp án B.
-
A.
6,4.
-
B.
3,6.
-
C.
17,7.
-
D.
5,6.
Đáp án : B
Dựa vào kiến thức về hai tam giác vuông đồng dạng để tìm x.
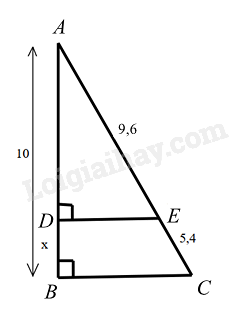
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(\widehat B = \widehat D = {90^0}\)
\(\widehat A\) chung
Suy ra $\Delta ABC\backsim \Delta ADE$ (g.g)
Do đó \(\frac{{AB}}{{BC}} = \frac{{AD}}{{DE}}\) hay \(\frac{{10}}{{9,6 + 5,4}} = \frac{{AD}}{{9,6}}\)
Suy ra \(AD = 9,6.\frac{{10}}{{9,6 + 5,4}} = 6,4\)
Vậy \(x = AB - AD = 10 - 6,4 = 3,6\).
Đáp án B.
Trong các hình sau, cặp hình nào không phải luôn đồng dạng?
-
A.
Tam giác cân.
-
B.
Hình tròn.
-
C.
Tam giác đều.
-
D.
Hình vuông.
Đáp án : A
Dựa vào đặc điểm của các hình để xác định.
Tam giác cân không phải luôn đồng dạng.
Đáp án A.
-
A.
\(k = \frac{1}{2}\).
-
B.
\(k = 1\).
-
C.
\(k = 2\).
-
D.
\(k = 4\).
Đáp án : A
Dựa vào số đo các cạnh để tìm tỉ số.
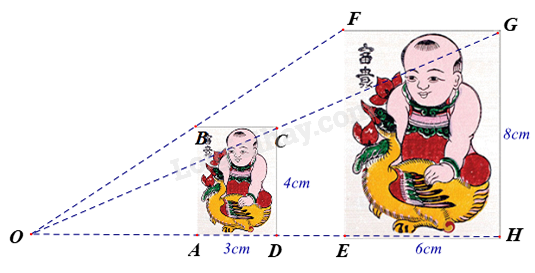
Ta có: \(\frac{3}{6} = \frac{4}{8} = \frac{1}{2}\) nên hình ABCD đồng dạng phối cảnh với hình EFGH theo tỉ số đồng dạng là \(k = \frac{1}{2}\).
Đáp án A.
1. Đưa phương trình về dạng \(ax + b = 0\) để giải.
a) Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song nếu \(a = a';b \ne b'\).
b) Viết phương trình hoành độ giao điểm của hai đường thẳng.
2. Điểm nằm trên trục tung có hoành độ bằng 0.
1. a) \(3\left( {x - 1} \right) - 7 = 5\left( {x + 2} \right)\)
\(\begin{array}{l}3x - 3 - 7 = 5x + 10\\3x - 5x = 10 + 3 + 7\\ - 2x = 20\\x = - 10\end{array}\)
Vậy \(x = - 10\)
b) \(\frac{{x + 4}}{5} - x + 4 = \frac{x}{3} - \frac{{x - 2}}{2}\)
\(\begin{array}{l}\frac{{6\left( {x + 4} \right)}}{{30}} - \frac{{30\left( {x - 4} \right)}}{{30}} = \frac{{10x}}{{30}} - \frac{{15\left( {x - 2} \right)}}{{30}}\\6\left( {x + 4} \right) - 30\left( {x - 4} \right) = 10x - 15\left( {x - 2} \right)\\6x + 24 - 30x + 120 = 10x - 15x + 30\\6x - 30x - 10x + 15x = 30 - 24 - 120\\ - 19x = - 114\\x = 6\end{array}\)
Vậy \(x = 6\)
2. a) Để đường thẳng (d) song song với đường thẳng \(\left( {{d_1}} \right):y = 3 - 2x\) thì \(\left\{ \begin{array}{l}m - 1 = - 2\\4 \ne 3\end{array} \right.\) hay \(m = - 1\).
b) Phương trình hoành độ giao điểm hai đường thẳng \(\left( d \right)\) và \(\left( {{d_2}} \right)\) là:
\(\begin{array}{l}\left( {m - 1} \right)x + 4 = x + m\\mx - x + 4 = x + m\\mx - x - x = m - 4\\x\left( {m - 2} \right) = m - 4\\x = \frac{{m - 4}}{{m - 2}}\end{array}\)
Vì đường thẳng (d) cắt đường thẳng \(\left( {{d_2}} \right):y = x + m\) tại một điểm nằm trên trục tung nên giao điểm của hai đường thẳng có hoành độ bằng 0, hay \(\frac{{m - 4}}{{m - 2}} = 0\) suy ra \(m = 4\).
Vậy với m = 4 thì đường thẳng (d) cắt đường thẳng \(\left( {{d_2}} \right):y = x + m\) tại một điểm nằm trên trục tung.
Giải bài toán bằng cách lập phương trình.
Gọi chiều rộng của hình chữ nhật là x (x > 0)
Biểu diễn chiều dài của hình chữ nhật, các cạnh của hình chữ nhật sau khi thay đổi và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi chiều rộng của hình chữ nhật là x (m) (x > 0).
Vì chiều dài hơn chiều rộng 7m nên đồ dài chiều dài là: x + 7 (m)
Khi đó diện tích hình chữ nhật lúc đầu là: x(x + 7)
Vì khi tăng chiều rộng lên gấp 3 lần và tăng chiều dài thêm 5m thì mảnh đất thành hình vuông nên ta có phương trình:
3x = x + 7 + 5 hay 2x – 12 = 0
Giải phương trình ta được x = 6 (m) (TM)
Vậy diện tích hình chữ nhật lúc đầu là: 6.(6 + 7) = 78\({m^2}\).
1. Tính thể tích của một nhà kính bằng công thức tính thể tích hình chóp tứ giác đều.
2. a) Chứng minh $\Delta ABE\backsim \Delta ACF$ theo trường hợp góc – góc suy ra tỉ số các cạnh tương ứng suy ra \(AE.AC = AF.AB\).
b) Chứng minh $\Delta ANB\backsim \Delta ENA$ (g.g) suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{N^2} = NE.NB\).
c) Dựa vào các tỉ số của câu a và b suy ra \(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\) suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$.
Từ đó suy ra số đo góc AMB.
1.
Vì mỗi nhà kính lớn có dạng hình chóp tứ giác đều nên thể tích một nhà kính là:
\(\frac{1}{3}.24.660 = 5280\left( {{m^3}} \right)\)
Thể tích hai nhà kính này là:
\(2.5280 = 10560\left( {{m^3}} \right)\)
2.
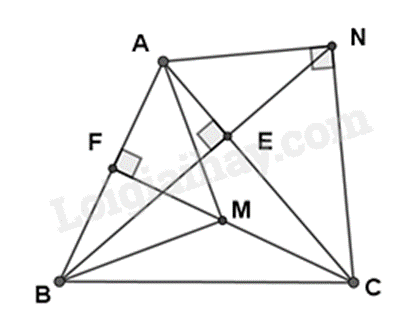
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat {AEB} = \widehat {AFC} = {90^0}\)
\(\widehat {BAC}\) chung
Suy ra $\Delta ABE\backsim \Delta ACF$ (g.g). (đpcm)
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\) hay \(AB.AF = AE.AC\)(đpcm) (1)
b) Xét \(\Delta ANE\) và \(\Delta ACN\) có:
\(\widehat {AEN} = \widehat {ANC} = {90^0}\)
\(\widehat {NAC}\) chung
Suy ra $\Delta ANE\backsim \Delta ACN$ (g.g).
Suy ra \(\frac{{AN}}{{AC}} = \frac{{AE}}{{AN}}\) hay \(A{N^2} = AC.AE\) (đpcm). (2)
c) Từ (1) và (2) suy ra \(AB.AF = A{N^2}\).
Mà AM = AN (gt) suy ra \(AM = AB.AF\) hay \(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\).
Xét \(\Delta AMF\) và \(\Delta ABM\) có:
\(\widehat {BAM}\) chung
\(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\) (cmt)
Suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$
Suy ra \(\widehat {AMB} = \widehat {AFM} = {90^0}\).
Tính số kết quả thuận lợi cho biến cố “Học sinh được chọn là nam và không học lớp 7”.
Tính xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi với tổng số kết quả có thể.
Số học sinh là nam và không học lớp 7 là:
8 + 4 + 4 = 16 (học sinh)
Có 16 kết quả thuận lợi cho biến cố “Học sinh được chọn là nam và không học lớp 7”.
Tổng số kết quả có thể là:
8 + 9 + 6 + 8 + 4 + 5 + 4 + 3 = 47
Vậy xác suất của biến cố “Học sinh được chọn là nam và không học lớp 7” là: \(\frac{{16}}{{47}}\).
Nhân cả hai vế của phương trình với 9, phương trình trở thành \(\left( {3x - 2} \right){\left( {3x + 3} \right)^2}\left( {3x + 8} \right) = - 144\).
Đặt \(3x + 3 = t\), biến đổi phương trình thành \(\left( {t - 5} \right){t^2}\left( {t + 5} \right) = - 144\).
Giải phương trình ta được các giá trị của t.
Thay \(t = 3x + 3\) ta tìm đc x.
Nhân cả hai vế của phương trình \(\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16\) với 9, ta được:
\(\begin{array}{l}9.\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16.9\\\left( {3x - 2} \right){\left[ {3\left( {x + 1} \right)} \right]^2}\left( {3x + 8} \right) = - 144\\\left( {3x - 2} \right){\left( {3x + 3} \right)^2}\left( {3x + 8} \right) = - 144\end{array}\)
Đặt \(3x + 3 = t\) suy ra \(3x - 2 = t - 5\); \(3x + 8 = t + 5\)
Ta được phương trình biến t như sau:
\(\left( {t - 5} \right){t^2}\left( {t + 5} \right) = - 144\)
\(\begin{array}{l}{t^4} - 25{t^2} + 144 = 0\\\left( {{t^2} - 9} \right)\left( {{t^2} - 16} \right) = 0\\\left[ \begin{array}{l}{t^2} = 9\\{t^2} = 16\end{array} \right.\\\left[ \begin{array}{l}t = \pm 3\\t = \pm 4\end{array} \right.\end{array}\)
Thay \(t = 3x + 3\) ta được:
Vậy nghiệm của phương trình là \(x \in \left\{ {0; - 2;\frac{1}{3};\frac{{ - 7}}{3}} \right\}\).
Phần trắc nghiệm (3 điểm) Câu 1: Để giải phương trình $\frac{2x-3}{4}-\frac{1-x}{5}=1$, một bạn học sinh thực hiện như sau:
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn là
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
A. NỘI DUNG ÔN TẬP Đại số Phương trình bậc nhất và hàm số bậc nhất - Phương trình bậc nhất một ẩn - Giải bài toán bằng cách lập phương trình - Khái niệm hàm số và đồ thị của hàm số - Hàm số bậc nhất và đồ thị của hàm số bậc nhất - Hệ số góc của đường thẳng
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
