Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 7. Tính chất đường trung trực của một đoạn thẳng
Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 3 – Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 3 – Hình học 7
Đề bài
Cho góc \(\widehat {xOy} = {60^0}\), một điểm M nằm trong góc đó. Lấy điểm N sao cho Ox là trung trực của đoạn MN, lấy P sao cho Oy là trung trực của MP.
a) Chứng minh \(\Delta NOP\) cân.
b) Tính số đo góc \(\widehat {NOP}\).
Phương pháp giải - Xem chi tiết
Điểm thuộc đường trung trực của 1 đoạn thẳng thì cách đều 2 đầu mút
Lời giải chi tiết
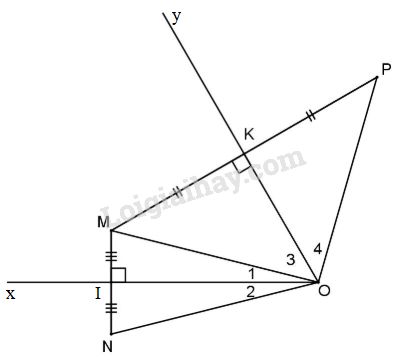
a) O thuộc trung trực của đoạn MN nên
OM = ON (1).
Lại có O thuộc trung trực của đoạn MP nên \(MO = PO\) (2).
Từ (1) và (2) \( \Rightarrow ON = OP,\) hay \(\Delta NOP\) cân tại O.
b) (Xem hình vẽ). Dễ thấy
\(\Delta OIM = \Delta OIN\) và \(\Delta OKP = \Delta OKM\) (c.g.c)
\( \Rightarrow {\widehat O_1} = {\widehat O_2}\) và \({\widehat O_3} = {\widehat O_4}\) mà \({\widehat O_1} + {\widehat O_3} = {60^0}\)
\( \Rightarrow {\widehat O_1} + {\widehat O_2} + {\widehat O_3} + {\widehat O_4} = {120^0}.\)
Hay \(\widehat {NOP} = {120^0}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 8 - Bài 7 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 9 - Bài 7 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 3 – Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
