Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng t..
Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 3 – Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 3 – Hình học 7
Đề bài
Cho tam giác ABC, điểm M nằm trong tam giác. Gọi I là giao điểm của BM và AC. Chứng minh rằng: \(MA + MB < IA + IB < CA + CB.\)
Phương pháp giải - Xem chi tiết
Trong một tam giác độ dài 1 cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại
Lời giải chi tiết
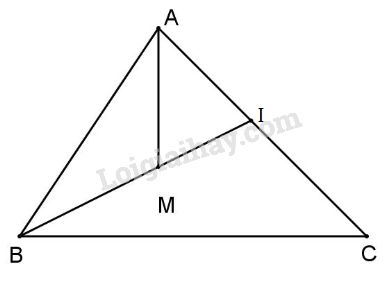
Xét \(\Delta AMI\), theo bất đẳng thức tam giác
\(\eqalign{ & MA < MI + IA \cr& \Rightarrow MA + MB < MI + IA + MB \cr & \Rightarrow MA + MB < IA + IB{\rm{ \;\;\;\;\; (1)}} \cr} \)
Xét \(\Delta {\rm B}{\rm I}C\), ta có \(IB < IC + BC\)
\(\eqalign{ & \Rightarrow IB + IA < IC + BC + IA \cr & \Rightarrow IB + IA < AC + BC{\rm{ \;\;\;\;\;\;\;\; (2)}} \cr} \)
Từ (1) và (2) ta có \(MA + MB < IA + IB < AC + BC.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 3 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 3 – Hình học 7
- Bài 22 trang 64 SGK Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
