Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 1 - Đại số 7
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 1 - Đại số 7
Đề bài
Bài 1: Điền vào kí hiệu ( \(∈, \notin \), \(\subset \)) thích hợp vào ô trống:
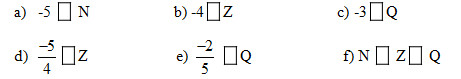
Bài 2: Viết các số hữu tỉ sau dưới dạng phân số có mẫu số dương:
a) \({5 \over { - 3}}\);
b) \({{ - 18} \over {45}}\);
c) \({{ - 7777} \over { - 1111}}\)
Bài 3: So sánh :
a) \({5 \over { - 3}}\) và \({{ - 15} \over 9}\)
b) \({{ - 12} \over { - 39}}\) và \({{36} \over {117}}\).
LG bài 1
Phương pháp giải:
Sử dụng các tập hợp số.
Số hữu tỉ là số có thể viết dưới dạng \(\dfrac{a}{b}\) với \(a, b ∈ \mathbb Z, b \ne 0\) và được kí hiệu là \(\mathbb Q\)
Lời giải chi tiết:
LG bài 2
Phương pháp giải:
Sử dụng: \(\frac{a}{{ - b}} = \frac{{ - a}}{b} = - \frac{a}{b}\)
Lời giải chi tiết:
a) \({5 \over { - 3}}\)= \({{ - 5} \over 3}\)
b) \({{ - 18} \over {45}}\)=\({{ - 2} \over 5}\)
c) \({{ - 7777} \over {1111}}\)=\({{7777} \over {1111}}\)=7
LG bài 3
Phương pháp giải:
Để so sánh hai số hữu tỉ \(x,y\) ta làm như sau:
- Viết \(x,y\) dưới dạng phân số cùng mẫu dương.
\(x = \dfrac{a}{m} ; y = \dfrac{b}{m} ( m>0)\)
- So sánh các tử là số nguyên \(a\) và \(b\)
Nếu \(a> b\) thì \(x > y\)
Nếu \(a = b\) thì \(x=y\)
Nếu \(a < b\) thì \(x < y\).
Lời giải chi tiết:
a) Ta có: \({{ - 15} \over 9}\)=\({{( - 15):3} \over {9:3}}\)=\({{ - 5} \over 3}\)=\({5 \over { - 3}}\).
Vậy \({5 \over { - 3}}\)=\({{ - 15} \over 9}\)
b) Ta có: \({{ - 12} \over { - 39}}\)=\({{( - 12).3} \over {( - 39).3}}\)=\({{ - 36} \over { - 117}}\)=\({{36} \over {117}}\).
Vậy \({{ - 12} \over { - 39}}\)=\({{36} \over {117}}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Đại số 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Đại số 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 1 - Đại số 7
- Đề kiểm tra 15 phút - Đề số 6 - Bài 1 - Chương 1 - Đại số 7
- Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Đại số 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
