Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 9. Tính chất ba đường cao của tam giác
Đề kiểm tra 15 phút - Đề số 1 - Bài 9 - Chương 3 – Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 9 - Chương 3 – Hình học 7
Đề bài
Cho tam giác ABC (AB = AC), hai đường cao BE và CF cắt nhau tại H (E thuộc AC và F thuộc AB). Tia AH cắt BC ở I. Chứng minh:
a) I là trung điểm của BC.
b) cân.
Phương pháp giải - Xem chi tiết
Cho tam giác ABC cân tại A, trung tuyến xuất phát từ đỉnh A đồng thời là đường cao.
Lời giải chi tiết
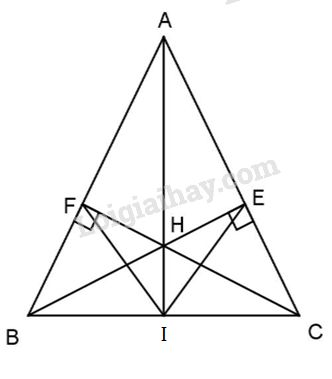
a) Hai đường cao BE và CF cắt nhau tại H nên H là trực tâm của . Do đó AH là đường cao thứ ba, AH cắt BC ở I nên
cân tại A (gt) đường cao AI đồng thời là đường trung tuyến , hay I là trung điểm của BC.
b) Hai tam giác vuông BFC và CEB có trung cạnh huyền BC nên hai trung tuyến: hay cân.
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 2 - Bài 9 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 9 - Chương 3 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 9 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 9 - Chương 3 – Hình học 7
- Bài 62 trang 83 SGK Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 7 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
