 Toán nâng cao lớp 5 - Bài tập toán nâng cao lớp 5 có lời giải
Toán nâng cao lớp 5 - Bài tập toán nâng cao lớp 5 có lời giải
 Giải chuyên đề 11: Các bài toán về chuyển động đều Toán..
Giải chuyên đề 11: Các bài toán về chuyển động đều Toán.. Dạng 3: Bài toán về hai chuyển động ngược chiều - Toán nâng cao lớp 5
Tải vềLúc 5 giờ sáng bạn Nam đi xe đạp từ A về B với vận tốc 12 km/giờ. Đến 8 giờ, bạn Việt đi xe đạp từ B về A với vận tốc 15 km/giờ. Lúc 12 giờ trưa một ô tô khởi hành từ A đi về B. Cùng lúc đó một xe máy khởi hành từ B đi về A và hai xe gặp nhau tại địa điểm C cách A 180 km.
|
Phương pháp giải: Hai vật chuyển động ngược chiều với vận tốc v1 và v2, cùng thời điểm xuất phát và cách nhau quãng đường bằng s thì thời gian để chúng đi đến chỗ gặp nhau là: t = s : (v1 + v2) |
Ví dụ 1: Lúc 5 giờ sáng bạn Nam đi xe đạp từ A về B với vận tốc 12 km/giờ. Đến 8 giờ, bạn Việt đi xe đạp từ B về A với vận tốc 15 km/giờ. Hỏi 2 người gặp nhau lúc mấy giờ? Biết quãng đường AB dài 117 km. Địa điểm gặp nhau cách A bao nhiêu ki-lô-mét?
Giải
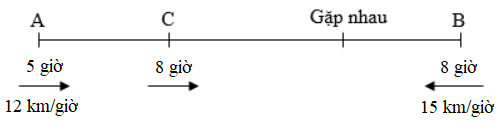
Thời gian bạn Nam đi trước là
8 – 5 = 3 (giờ)
Sau 3 giờ bạn Nam đi được quãng đường là
12 x 3 = 36 (km)
Khi đó, hai người còn cách nhau:
117 – 36 = 81 (km)
Thời gian từ lúc bạn Việt đi đến lúc gặp nhau là
81 : (12 + 15) = 3 (giờ)
Thời điểm hai người gặp nhau là
8 + 3 = 11 (giờ)
Địa điểm gặp nhau cách A số ki-lô-mét là
36 + 12 x 3 = 72 (km)
Đáp số: 11 giờ
72 km
Ví dụ 2: Lúc 12 giờ trưa một ô tô khởi hành từ A đi về B. Cùng lúc đó một xe máy khởi hành từ B đi về A và hai xe gặp nhau tại địa điểm C cách A 180 km. Tính vận tốc của mỗi xe, biết rằng vận tốc của ô tô lớn hơn vận tốc của xe máy là 15km/giờ và quãng đường AB dài 300km.
Giải
Quãng đường xe máy đi đến chỗ gặp nhau là:
300 – 180 = 120 (km)
Đến khi gặp nhau, tỉ số giữa quãng đường ô tô đi được và xe máy đi được là:
$180:120 = \frac{3}{2}$
Trong cùng một thời gian, quãng đường và vận tốc là hai đại lượng tỉ lệ thuận.
Suy ra tỉ số giữa vận tốc của ô tô và vận tốc của xe máy là $\frac{3}{2}$.
Ta có sơ đồ sau:
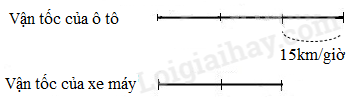
Vận tốc của ô tô là:
15 : (3 – 2) x 3 = 45 (km/giờ)
Vận tốc của xe máy là
45 – 15 = 30 (km//giờ)
Đáp số: Ô tô 45km/giờ ; xe máy: 30km/giờ
Ví dụ 3: Xe thứ nhất đi từ A đến B hết 3 giờ, xe thứ hai đi từ A đến B hết 2 giờ. Nếu lúc 10 giờ hai xe cùng khởi hành, xe thứ nhất xuất phát từ A đi đến B và xe thứ hai đi từ B về A thì lúc mấy giờ hai xe sẽ gặp nhau?
Giải
Xe thứ nhất đi từ A đến B hết 3 giờ nên 1 giờ xe thứ nhất đi được $\frac{1}{3}$ quãng đường AB.
Xe thứ hai đi từ A đến B hết 2 giờ nên 1 giờ xe thứ hai đi được $\frac{1}{2}$ quãng đường AB.
Trong 1 giờ cả 2 xe đi được:
$\frac{1}{3} + \frac{1}{2} = \frac{5}{6}$ (quãng đường AB)
Thời gian để hai xe đi đến chỗ gặp nhau là:
$1:\frac{5}{6} = 1,2$ (giờ)
1,2 giờ = 1 giờ 12 phút
Thời điểm hai xe gặp nhau là:
10 giờ + 1 giờ 12 phút = 11 giờ 12 phút
Đáp số: 11 giờ 12 phút
BÀI TẬP ÁP DỤNG
Hai thành phố A và B cách nhau 135 km. Một xe máy đi từ A đến B với vận tốc 42km/h và một xe đạp đi từ B đến A với vận tốc 12km/h. Hỏi sau bao lâu xe đạp và xe máy gặp nhau. Lúc gặp nhau xe máy cách B bao nhiêu km?
Hai thành phố A và B cách nhau 186 km. Lúc 6 giờ một người đi xe máy từ A với vận tốc 30km/giờ về B. Lúc 7 giờ một người khác đi xe máy từ B với vận tốc 35km/giờ về A. Hỏi lúc mấy giờ thì hai người gặp nhau và chỗ gặp nhau cách A bao xa?
Hai ô tô xuất phát từ A và B cùng một lúc và đi ngược chiều nhau. Quãng đường AB dài 162 km. Sau 2 giờ chúng gặp nhau. Tìm vận tốc của mỗi ô tô, biết vận tốc ô tô đi từ A bằng $\frac{4}{5}$ vận tốc ô tô đi từ B. Điểm gặp nhau cách A bao nhiêu km?
Một ô tô khởi hành tại A lúc 4 giờ sáng đi về B với vận tốc 60 km/h. Đến 5 giờ ô tô khác khởi hành tại B và đi về A với vận tốc 70 km/h. Hai xe gặp nhau lúc 8h. Tính khoảng cách từ A đến B.
Lúc 7 giờ sáng, một xe ô tô khởi hành từ A để đi về B với vận tốc 65km/giờ. Đến 8 giờ 30 phút một ô tô khác xuất phát từ B đi về A với vận tốc 75 km/giờ. Hỏi hai xe gặp nhau vào lúc mấy giờ? Biết rằng A cách B là 657,5 km.
- Dạng 4: Vật chuyển động trên dòng nước - Toán nâng cao lớp 5
- Dạng 5: Vật chuyển động có chiều dài đáng kể - Toán nâng cao lớp 5
- Bài tập tự luyện: Các bài toán về chuyển động đều - Toán nâng cao lớp 5
- Dạng 2: Bài toán về hai chuyển động cùng chiều - Toán nâng cao lớp 5
- Dạng 1: Các bài toán có một chuyển động tham gia - Toán nâng cao lớp 5
>> Xem thêm
Các bài khác cùng chuyên mục
- Bài tập tự luyện: Các bài toán về tính tuổi - Toán nâng cao lớp 5
- Dạng 2: Cho biết hiệu và tỉ số tuổi của hai người - Toán nâng cao lớp 5
- Dạng 1: Cho biết tổng và tỉ số tuổi của hai người - Toán nâng cao lớp 5
- Dạng 7: Tỉ số phần trăm dạng hạt tươi, hạt khô - Toán nâng cao lớp 5
- Dạng 6: Bài toán tăng, giảm tỉ số phần trăm - Toán nâng cao lớp 5
- Bài tập tự luyện: Các bài toán về tính tuổi - Toán nâng cao lớp 5
- Dạng 2: Cho biết hiệu và tỉ số tuổi của hai người - Toán nâng cao lớp 5
- Dạng 1: Cho biết tổng và tỉ số tuổi của hai người - Toán nâng cao lớp 5
- Dạng 7: Tỉ số phần trăm dạng hạt tươi, hạt khô - Toán nâng cao lớp 5
- Dạng 6: Bài toán tăng, giảm tỉ số phần trăm - Toán nâng cao lớp 5












Danh sách bình luận