Câu 3 trang 43 SGK Vật Lý 12 Nâng cao

Tính thế năng, động năng và cơ năng của con lắc đơn ở một vị trí bất kì

Đề bài

Tính thế năng, động năng và cơ năng của con lắc đơn ở một vị trí bất kì (li độ góc \(\alpha \)) và thử lại rằng cơ năng không đổi trong chuyển động.

Lời giải chi tiết

Xét con lắc đơn, ở một vị trí bất kì (có li độ góc \(\alpha \))

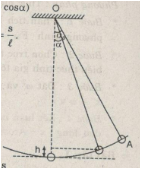
a) Biểu thức thế năng : \({W_t} = mgh = mg\ell (1 - \cos \alpha )\)

Với dao động nhỏ :\(1 - \cos \alpha = {{{\alpha ^2}} \over 2}\text{ và }\alpha = {s \over \ell }.\)

Thay vào \( \Rightarrow {W_t} = {1 \over 2}m{g \over \ell }{s^2} = {1 \over 2}m{\omega ^2}{s^2}\)

b) Biểu thức động năng :\({W_đ} = {1 \over 2}m{v^2}\)

với \({v^2} = 2g\ell (\cos \alpha - \cos {\alpha _0}).\)

Dao động nhỏ :

\(1 - \cos \alpha = {{{\alpha ^2}} \over 2};1 - \cos {\alpha _0} = {{\alpha _0^2} \over 2}\) và \(\alpha = {s \over \ell }.\)

Thay vào :\({W_đ} = {1 \over 2}m{\omega ^2}(s_0^2 - {s^2}).\)

c) Cơ năng :\(W = {W_đ} + {W_t} = {1 \over 2}m{\omega ^2}(s_0^2 - {s^2}) - {1 \over 2}m{\omega ^2}{s^2}\)

\( \Rightarrow {W} = {1 \over 2}m{\omega ^2}s_0^2\) không đổi trong chuyển động.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.4 trên 5 phiếu

Bài tiếp theo

Câu 4 trang 43 SGK Vật Lý 12 Nâng cao
Dựa vào định luật bảo toàn cơ năng, tính :Dựa vào định luật bảo toàn cơ năng, tính :
Câu 2 trang 43 SGK Vật Lý 12 Nâng cao
Một vật có khối lượng 750g dao động điều hoà
Câu 1 trang 43 SGK Vật Lý 12 Nâng cao
Động năng của vật nặng dao động điều hoà biến đổi theo thời gian