Số giá trị nguyên của tham số \(m\) để phương trình \(\sin 2x + \sqrt[{}]{2}\sin \left( {x + \dfrac{\pi }{4}} \right) - 2 = m\) có đúng một nghiệm thực thuộc khoảng \(\left( {0\,;\,\dfrac{{3\pi }}{4}} \right)\)?
-
A.
$3$.
-
B.
$2$.
-
C.
$0$.
-
D.
$1$.
- Đặt \(\sin x + \cos x = t\) tìm điều kiện của \(t\), đưa phương trình về phương trình bậc hai ẩn \(t\)
- Biện luận số nghiệm của phương trình đã cho theo số nghiệm của phương trình ẩn \(t\) , sử dụng tương giao đồ thị.
Ta có \(x \in \left( {0\,;\,\dfrac{{3\pi }}{4}} \right)\)\( \Rightarrow \dfrac{\pi }{4} < x + \dfrac{\pi }{4} < \pi \)\( \Rightarrow 0 < \sin \left( {x + \dfrac{\pi }{4}} \right) \le 1\)\( \Rightarrow 0 < \sqrt[{}]{2}\sin \left( {x + \dfrac{\pi }{4}} \right) \le \sqrt[{}]{2}\).
Mặt khác \(\sqrt[{}]{2}\sin \left( {x + \dfrac{\pi }{4}} \right) = \sin x + \cos x\).
Đặt \(\sin x + \cos x = t\) với \(t \in \left( {0\,;\,\sqrt[{}]{2}} \right]\)\( \Rightarrow {\sin ^2}x + {\cos ^2}x + 2\sin x.\cos x = {t^2}\) \( \Rightarrow \sin 2x = {t^2} - 1\).
Nhận thấy với mỗi giá trị của \(t\) trong \(\left( {0;1} \right]\) hoặc \(t = \sqrt 2 \) thì đều có một giá trị của \(x \in \left( {0;\dfrac{{3\pi }}{4}} \right)\), nếu \(t \in \left[ {1;\sqrt 2 } \right)\) thì sẽ có \(2\) giá trị của \(x \in \left( {0;\dfrac{{3\pi }}{4}} \right)\)
Phương trình đã cho trở thành \({t^2} - 1 + t - 2 = m \Leftrightarrow {t^2} + t - 3 = m\)\(\left( * \right)\).
Xét \(f\left( t \right) = {t^2} + t - 3\) với \(t \in \left( {0\,;\,\sqrt[{}]{2}} \right]\) có đồ thị là parabol, hoành độ đỉnh \(t = - \dfrac{1}{2} \notin \left( {0;\sqrt 2 } \right]\)
Bảng biến thiên:
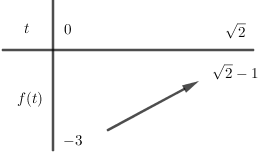
Dựa vào bảng biến thiên ta có phương trình \(\left( * \right)\) có nhiều nhất một nghiệm \(t\).
Do đó để phương trình đã cho có đúng một nghiệm thực \(x\) thuộc khoảng \(\left( {0\,;\,\dfrac{{3\pi }}{4}} \right)\) thì $\left[ \begin{array}{l}t = \sqrt[{}]{2}\\0 < t \le 1\end{array} \right.$.
Với \(t = \sqrt[{}]{2}\) thay vào phương trình \(\left( * \right)\): \(2 + \sqrt[{}]{2} - 3 = m\)\( \Leftrightarrow m = \sqrt[{}]{2} - 1 \notin \mathbb{Z}\).
Với $0 < t \le 1$ ta có bảng biến thiên
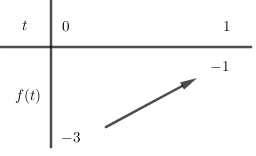
Vậy \( - 3 < m \le - 1\)\( \Rightarrow \) có \(2\) giá trị nguyên của \(m\) là \( - 2\) và \( - 1\).
Đáp án : B
Các bài tập cùng chuyên đề
Phương trình \(\sqrt {1 + \sin x} + \sqrt {1 + \cos x} = m\) có nghiệm khi và chỉ khi
Gọi \(S\) là tổng tất cả các nghiệm thuộc \(\left[ {0;20\pi } \right]\) của phương trình\(2{\cos ^2}x - \sin x - 1 = 0\). Khi đó, giá trị của \(S\) bằng :
Gọi \(S\) là tập hợp các nghiệm thuộc khoảng \(\left( {0;100\pi } \right)\) của phương trình \({\left( {\sin \dfrac{x}{2} + \cos \dfrac{x}{2}} \right)^2} + \sqrt 3 \cos x = 3\). Tổng các phần tử của \(S\) là
Tổng các nghiệm của phương trình \(2\cos 3x\left( {2\cos 2x + 1} \right) = 1\) trên đoạn \(\left[ { - 4\pi ;6\pi } \right]\) là:
Số nghiệm thuộc đoạn $\left[ {0;2017} \right]$ của phương trình \(\dfrac{{\sqrt {1 + \cos x} + \sqrt {1 - \cos x} }}{{\sin x}} = 4\cos x\) là
Gọi \(M\), \(m\) lần lượt là giá lớn nhất, giá trị nhỏ nhất của hàm số $y = {\sin ^{2018}}x + {\cos ^{2018}}x$ trên \(\mathbb{R}\). Khi đó:
Tìm \(m\) để phương trình \(2{\sin ^2}x - \left( {2m + 1} \right)\sin x + 2m - 1 = 0\) có nghiệm thuộc khoảng \(\left( { - \dfrac{\pi }{2};0} \right)\).
Số các giá trị nguyên của \(m\) để phương trình \({\cos ^2}x + \sqrt {\cos x + m} = m\) có nghiệm là:
Số nghiệm của phương trình: ${\sin ^{2015}}x - {\cos ^{2016}}x = 2\left( {{{\sin }^{2017}}x - {{\cos }^{2018}}x} \right) + \cos 2x$ trên $\left[ { - 10;30} \right]$ là:
Cho phương trình \(\left( {1 + \cos x} \right)\left( {\cos 4x - m\cos x} \right) = m{\sin ^2}x\). Tìm tất cả các giá trị của \(m\) để phương trình có đúng \(3\) nghiệm phân biệt thuộc \(\left[ {0\,;\,\dfrac{{2\pi }}{3}} \right]\).
Khẳng định nào sau đây là đúng về phương trình \(\sin \left( {\dfrac{x}{{{x^2} + 6}}} \right) + \cos \left( {\dfrac{\pi }{2} + \dfrac{{80}}{{{x^2} + 32x + 332}}} \right) = 0\)?
Gọi \(M,m\) lần lượt GTLN, GTNN của hàm số \(y = 2{\sin ^3}x + {\cos ^3}x\). Giá trị biểu thức \(T = {M^2} + {m^2}\) là:
