Số các giá trị nguyên của \(m\) để phương trình \({\cos ^2}x + \sqrt {\cos x + m} = m\) có nghiệm là:
-
A.
\(4\).
-
B.
\(2\).
-
C.
\(3\).
-
D.
\(5\).
- Đặt \(t = \sqrt {\cos + m} \) đưa phương trình về hệ phương trình
- Sử dụng phương pháp cộng đại số biến đổi hệ phương trình đưa về phương trình dạng tích.
- Tìm điều kiện để phương trình có nghiệm, sử dụng kiến thức của hàm số bậc hai.
Ta có: \({\cos ^2}x + \sqrt {\cos x + m} = m\) suy ra \(m \ge 0\).
Đặt \(\sqrt {\cos x + m} = t\), \(t \ge 0\). Phương trình trở thành: $\left\{ \begin{array}{l}{\cos ^2}x + t = m\\{t^2} - \cos x = m\end{array} \right.$
$ \Rightarrow \,\left( {{{\cos }^2}x - {t^2}} \right) + \left( {t + \cos x} \right) = 0$$ \Leftrightarrow \left( {\cos x + t} \right)\left( {\cos x - t + 1} \right) = 0$$ \Leftrightarrow \left[ \begin{array}{l}\cos x = - t\\\cos x - t + 1 = 0\end{array} \right.$
+) Trường hợp \(1\): \(\cos x = - t\) \( \Rightarrow \sqrt {\cos x + m} = - \cos x\) \( \Leftrightarrow \left\{ \begin{array}{l}\cos x \le 0\\{\cos ^2}x - \cos x = m\end{array} \right.\)
Đặt \(u = \cos x\)\(\left( { - 1 \le u \le 0} \right)\)
Xét hàm số \(f\left( u \right) = {u^2} - u\) trên đoạn \(\left[ { - 1;0} \right]\), có hoành độ đỉnh \(x = \dfrac{1}{2} \notin \left[ { - 1;0} \right]\) và bảng biến thiên:
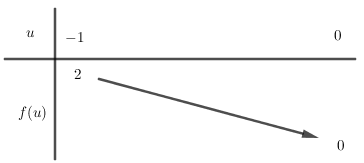
Để phương trình có nghiệm thì \(m \in \left[ {0;\,2} \right]\).
Vì \(m \in \mathbb{Z}\) nên \(m \in \left\{ {0;\,1;\,2} \right\}\).
+) Trường hợp \(2\): \(\cos x - t + 1 = 0\)\( \Leftrightarrow \sqrt {\cos x + m} = 1 + \cos x\)\( \Leftrightarrow {\cos ^2}x + \,\cos x + 1 = m\).
Đặt $v = \cos x$, $ - 1 \le v \le 1$. Ta có \(m = {v^2} + v + 1 = g\left( v \right)\)
Hàm số bậc hai \(g\left( v \right)\) có hoành độ đỉnh \(v = - \dfrac{1}{2} \in \left[ { - 1;1} \right]\) có bảng biến thiên :
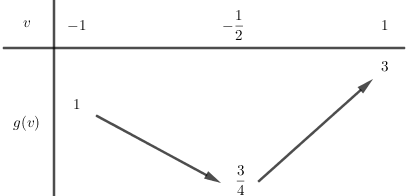
Để phương trình có nghiệm thì \(m \in \left[ {\dfrac{3}{4};3} \right]\).
Vì \(m \in \mathbb{Z}\) nên \(m \in \left\{ {1;\,2;\,3} \right\}\).
Vậy có tất cả \(4\) số nguyên \(m\) thỏa mãn bài toán.
Đáp án : A
Các bài tập cùng chuyên đề
Phương trình \(\sqrt {1 + \sin x} + \sqrt {1 + \cos x} = m\) có nghiệm khi và chỉ khi
Gọi \(S\) là tổng tất cả các nghiệm thuộc \(\left[ {0;20\pi } \right]\) của phương trình\(2{\cos ^2}x - \sin x - 1 = 0\). Khi đó, giá trị của \(S\) bằng :
Gọi \(S\) là tập hợp các nghiệm thuộc khoảng \(\left( {0;100\pi } \right)\) của phương trình \({\left( {\sin \dfrac{x}{2} + \cos \dfrac{x}{2}} \right)^2} + \sqrt 3 \cos x = 3\). Tổng các phần tử của \(S\) là
Tổng các nghiệm của phương trình \(2\cos 3x\left( {2\cos 2x + 1} \right) = 1\) trên đoạn \(\left[ { - 4\pi ;6\pi } \right]\) là:
Số nghiệm thuộc đoạn $\left[ {0;2017} \right]$ của phương trình \(\dfrac{{\sqrt {1 + \cos x} + \sqrt {1 - \cos x} }}{{\sin x}} = 4\cos x\) là
Gọi \(M\), \(m\) lần lượt là giá lớn nhất, giá trị nhỏ nhất của hàm số $y = {\sin ^{2018}}x + {\cos ^{2018}}x$ trên \(\mathbb{R}\). Khi đó:
Tìm \(m\) để phương trình \(2{\sin ^2}x - \left( {2m + 1} \right)\sin x + 2m - 1 = 0\) có nghiệm thuộc khoảng \(\left( { - \dfrac{\pi }{2};0} \right)\).
Số nghiệm của phương trình: ${\sin ^{2015}}x - {\cos ^{2016}}x = 2\left( {{{\sin }^{2017}}x - {{\cos }^{2018}}x} \right) + \cos 2x$ trên $\left[ { - 10;30} \right]$ là:
Số giá trị nguyên của tham số \(m\) để phương trình \(\sin 2x + \sqrt[{}]{2}\sin \left( {x + \dfrac{\pi }{4}} \right) - 2 = m\) có đúng một nghiệm thực thuộc khoảng \(\left( {0\,;\,\dfrac{{3\pi }}{4}} \right)\)?
Cho phương trình \(\left( {1 + \cos x} \right)\left( {\cos 4x - m\cos x} \right) = m{\sin ^2}x\). Tìm tất cả các giá trị của \(m\) để phương trình có đúng \(3\) nghiệm phân biệt thuộc \(\left[ {0\,;\,\dfrac{{2\pi }}{3}} \right]\).
Khẳng định nào sau đây là đúng về phương trình \(\sin \left( {\dfrac{x}{{{x^2} + 6}}} \right) + \cos \left( {\dfrac{\pi }{2} + \dfrac{{80}}{{{x^2} + 32x + 332}}} \right) = 0\)?
Gọi \(M,m\) lần lượt GTLN, GTNN của hàm số \(y = 2{\sin ^3}x + {\cos ^3}x\). Giá trị biểu thức \(T = {M^2} + {m^2}\) là:
