Bài 9 trang 12 SGK Hình học 10
Chứng minh rằng
Đề bài
Chứng minh rằng \(\overrightarrow{AB}= \overrightarrow{CD}\) khi và chỉ khi trung điểm của hai đoạn thẳng \(AD\) và \(BC\) trùng nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Với quy tắc ba điểm tùy ý \(A, \, \, B, \, \, C\) ta luôn có:
\(+ )\;\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm).
\( + )\;\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) (quy tắc trừ).
Lời giải chi tiết
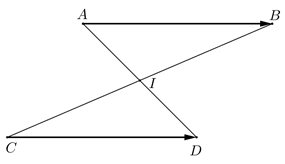
Ta chứng minh hai mệnh đề.
a) Cho \(\overrightarrow{AB}= \overrightarrow{CD}\) thì \(AD\) và \(BC\) có trung điểm trùng nhau.
Gọi \(I\) là trung điểm của \(AD\) ta chứng minh \(I\) cũng là trung điểm của \(BC\).
Theo quy tắc của ba điểm của tổng, ta có
\(\overrightarrow{AB}= \overrightarrow{AI} + \overrightarrow{IB}\);
\(\overrightarrow{CD}= \overrightarrow{CI}+ \overrightarrow{ID}\)
Vì \(\overrightarrow{AB} = \overrightarrow{CD}\) nên \(\overrightarrow{AI} + \overrightarrow{IB}= \overrightarrow{CI}+ \overrightarrow{ID}\)
\(\Rightarrow \overrightarrow{AI} - \overrightarrow{ID} = \overrightarrow{CI} - \overrightarrow{IB}\)
\(\Rightarrow\overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{CI} + \overrightarrow{BI}\) (1)
Vì \(I\) là trung điểm của \(AD\) nên \(\overrightarrow {IA} + \overrightarrow {ID} = \overrightarrow 0 \Leftrightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\) (2)
Từ (1) và (2) suy ra \(\overrightarrow{CI} + \overrightarrow{BI} = \overrightarrow{0} \Leftrightarrow \overrightarrow {IC} + \overrightarrow {IB} = \overrightarrow 0 \) (3)
Đẳng thức (3) chứng tỏ \(I\) là trung điểm của \(BC\).
b) \(AD\) và \(BC\) có cùng trung điểm \(I\), ta chứng minh \(\overrightarrow{AB}\) = \(\overrightarrow{CD}\).
\(I\) là trung điểm của \(AD\) \( \Leftrightarrow \overrightarrow {IA} + \overrightarrow {ID} = \overrightarrow 0 \Rightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\) \(\Rightarrow\overrightarrow{AI} - \overrightarrow{ID} =\overrightarrow{0}\)
\(I\) là trung điểm của \(BC\) \( \Leftrightarrow \overrightarrow {IC} + \overrightarrow {IB} = \overrightarrow 0 \) \(\Rightarrow \overrightarrow{CI} + \overrightarrow{BI}= \overrightarrow{0}\) \(\Rightarrow \overrightarrow{CI} - \overrightarrow{IB}= \overrightarrow{0}\)
Suy ra \(\overrightarrow{AI} - \overrightarrow{ID}= \overrightarrow{CI}- \overrightarrow{IB}\)
\(\Rightarrow \overrightarrow{AI} + \overrightarrow{IB} = \overrightarrow{CI}+ \overrightarrow{ID}\) \(\Rightarrow \overrightarrow{AB}= \overrightarrow{CD}\) (đpcm)
Cách khác:
Gọi trung điểm của AD là I, trung điểm BC là J.
Khi đó ta có: \(\overrightarrow {IA} + \overrightarrow {ID} = \overrightarrow 0 ,\overrightarrow {JB} + \overrightarrow {JC} = \overrightarrow 0 \)
Mà theo quy tắc ba điểm ta có:
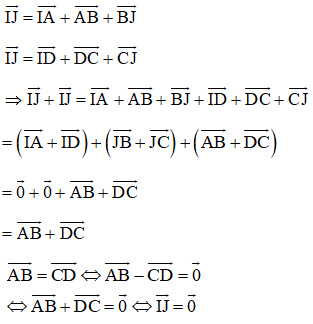
⇔ I ≡ J hay trung điểm AD và BC trùng nhau (đpcm).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 10 trang 12 SGK Hình học 10
- Bài 8 trang 12 SGK Hình học 10
- Bài 7 trang 12 SGK Hình học 10
- Bài 6 trang 12 SGK Hình học 10
- Bài 5 trang 12 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
