 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Bài 1. Tổng ba góc của một tam giác
Bài 1. Tổng ba góc của một tam giác
Bài 8 trang 109 SGK Toán 7 tập 1
Cho tam giác ABC có..
Đề bài
Cho tam giác \(ABC\) có \(\widehat{B}=\widehat{C}= 40^0\). Gọi \(Ax\) là tia phân giác của góc ngoài ở đỉnh \(A\), Hãy chứng tỏ \(Ax// BC\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
- Chứng minh hai đường thẳng song song ta chứng minh cặp góc so le trong bằng nhau.
Lời giải chi tiết
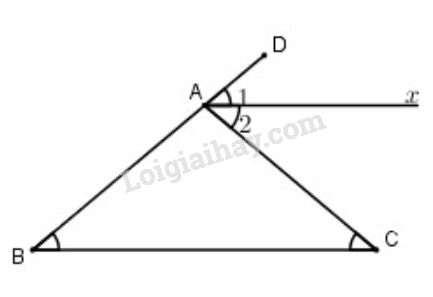
Cách 1:
Gọi \(\widehat{CAD} \) là góc ngoài tại đỉnh \(A\) của tam giác \(ABC\).
Ta có: \(\widehat{CAD } = \widehat{B}+ \widehat{C}\)\(= 40^0+ 40^0=80^0\) ( Góc ngoài bằng tổng 2 góc trong không kề với nó)
Lại có, \(Ax\) là phân giác \(\widehat{CAD }\)
nên \(\widehat{A_{2} }= \dfrac{1}2\widehat{CAD}=\dfrac{80^0}2=40^0\)
\( \Rightarrow \widehat {{A_2}}=\widehat{BCA }(=40^o\))
Mà hai góc này ở vị trí so le trong nên \(Ax// BC\).
Cách 2:
Gọi \(\widehat{CAD} \) là góc ngoài tại đỉnh \(A\) của tam giác \(ABC\)
\(\Rightarrow \widehat{CAD } = \widehat{B}+ \widehat{C} = 2.\widehat{B}\) ( vì \(\widehat{B}= \widehat{C}\))
Mà \(Ax\) là phân giác \(\widehat{CAD }\) nên \(\widehat{CAD} = 2. \widehat{DAx} \)
\(\Rightarrow \widehat{CAD } = \widehat{DAx} \)
Mà 2 góc này ở vị trí đồng vị
\(\Rightarrow Ax// BC\)




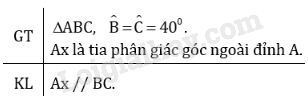








Danh sách bình luận