Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 1. Tổng ba góc của một tam giác
Bài 6 trang 109 SGK Toán 7 tập 1
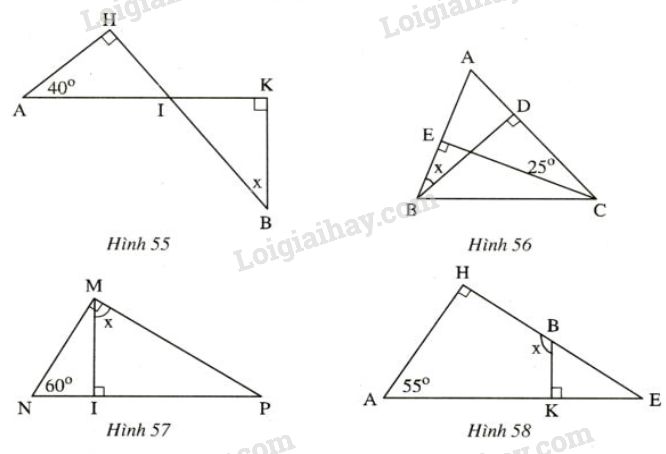
Tìm các số đo x ở các hình sau:
Đề bài
Tìm các số đo \(x\) ở các hình sau:
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Trong tam giác vuông có hai góc nhọn phụ nhau.
- Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
Lời giải chi tiết
Hình 55)
Xét \(\Delta AHI\,\text{ có }\,\widehat H = {90^0}\) ta có:
\(\widehat{A}+\widehat{AIH}= 90^0\) (1) (tổng hai góc nhọn của tam giác vuông bằng 90 độ)
Xét \(\Delta BKI\,\text{ có }\,\widehat K = {90^0}\) ta có:
\(\widehat{B} + \widehat{BIK} = 90^0\) (2) (tổng hai góc nhọn của tam giác vuông bằng 90 độ)
Từ (1) và (2) suy ra: \(\widehat{A}+\widehat{AIH}=\widehat{B} + \widehat{BIK}\)
Mà \(\widehat{AIH}= \widehat{BIK}\) (hai góc đối đỉnh)
Nên suy ra \( \widehat{B}=\widehat{A}=40^0\)
Vậy \(\widehat{B}=x= 40^0\)
Hình 56)
Xét \(\Delta ABD\,\text{ có }\,\widehat {ADB} = {90^0}\) ta có:
\(\widehat{ABD} +\widehat{A}= 90^0\) (4) (tổng hai góc nhọn của tam giác vuông bằng 90 độ)
Xét \(\Delta ACE\,\text{ có }\,\widehat {AEC} = {90^0}\) ta có:
\(\widehat{ACE}+ \widehat{A}=90^0\) (5) (tổng hai góc nhọn của tam giác vuông bằng 90 độ)
Từ (4) và (5) suy ra \(\widehat{ACE} = \widehat{ABD}=25^0\)
Vậy \(x=25^0\)
Hình 57)
Ta có: \(\widehat{NMP}=\widehat{NMI} + \widehat{PMI}= 90^0\) (6)
Xét \(\Delta MNI\,\text{ có }\,\widehat {MIN} = {90^0}\) ta có :
\(\widehat{N } + \widehat{NMI}= 90^0\) (7) (tổng hai góc nhọn của tam giác vuông bằng 90 độ)
Từ (6) và (7) suy ra \(\widehat{N } = \widehat{PMI}=60^0\)
Vậy \(x=60^0\)
Hình 58)
Xét \(\Delta AHE\,\text{ có }\,\widehat {AHE} = {90^0}\) ta có :
\(\widehat{E } + \widehat{A}=90^0\) (tổng hai góc nhọn của tam giác vuông bằng 90 độ)
\(\widehat{E }= 90^0- \widehat{A} = 90^0- 55^0= 35^0\)
Vì \(\widehat{KBH }\) là góc ngoài tại đỉnh \(B\) của tam giác \(BKE\) nên
\(\widehat{KBH }=\widehat{BKE}+ \widehat{E }\)\(= 90^0+ 35^0= 125^0\)
Vậy \(x=125^0\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 7 trang 109 SGK Toán 7 tập 1
- Bài 8 trang 109 SGK Toán 7 tập 1
- Bài 9 trang 109 SGK Toán 7 tập 1
- Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Hình học 7 (tập 1)
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
