Bài 5 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
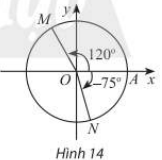
Viết công thức số đo tổng quát của các góc lượng giác (OA; OM) và \(\left( {OA;ON} \right)\) trong Hình 14
Đề bài
Viết công thức số đo tổng quát của các góc lượng giác (OA; OM) và \(\left( {OA;ON} \right)\) trong Hình 14:
Phương pháp giải - Xem chi tiết
Sử dụng công thức số đo tổng quát của góc lượng giác.
Lời giải chi tiết
Ta có
\[\left( {OA;{\rm{ }}OM} \right) = {120^ \circ } + k{.360^ \circ }\,\,(k \in Z)\]
\(\left( {OA;ON} \right) = - {75^ \circ } + k{.360^ \circ }\,\,(k \in Z)\)
- Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 7 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 8 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 9 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 4 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 136 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 130 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 121 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 113 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 107 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 136 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 130 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 121 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 113 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 107 SGK Toán 11 tập 1 - Chân trời sáng tạo













Danh sách bình luận