Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 7. Tính chất đường trung trực của một đoạn thẳng
Bài 48 trang 77 SGK Toán 7 tập 2
Hai điểm M và N cùng nằm trên một nửa mặt phẳng
Đề bài
Hai điểm \(M\) và \(N\) cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng \(xy.\) Lấy điểm \(L\) đối xứng với \(M\) qua \(xy.\) Gọi \(I\) là một điểm của \(xy.\) Hãy so sánh \(IM + IN\) với \(LN.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng tính chất đường trung trực của đoạn thẳng và bất đẳng thức tam giác.
Lời giải chi tiết
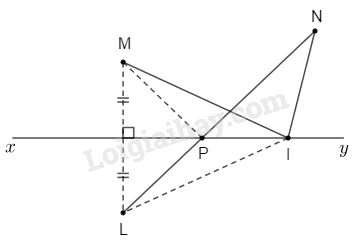
Gọi \(P\) là giao điểm của \(LN\) với \(xy.\)
Vì L và M đối xứng với nhau qua đường thẳng xy nên xy là đường thẳng đi qua trung điểm và vuông góc với ML.
Do đó, \(xy\) là đường trung trực của \(ML\)
Mà \(I \in xy\Rightarrow IM = IL\) (tính chất đường trung trực của đoạn thẳng)
- Nếu \(I\) không trùng \(P\) tức là ba điểm \(L,I,N\) không thẳng hàng
Xét \(ΔINL\) có \(IL + IN > LN\) (bất đẳng thức tam giác)
\(\Rightarrow IM + IN > LN\).
- Nếu \(I ≡ P\) tức là ba điểm \(L,I,N\) thẳng hàng, suy ra: \(IL + IN = LN\).
Khi đó: \(IM + IN = IL + IN = LN\) (vì \(IM=IL)\)
Vậy với mọi vị trí của \(I\) trên \(xy\) thì \(IM + IN ≥ LN.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 49 trang 77 SGK Toán 7 tập 2
- Bài 50 trang 77 SGK Toán 7 tập 2
- Bài 51 trang 77 SGK Toán 7 tập 2
- Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 3 – Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
