Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 7. Tính chất đường trung trực của một đoạn thẳng
Bài 45 trang 76 SGK Toán 7 tập 2
Chứng minh đường thẳng PQ..
Đề bài
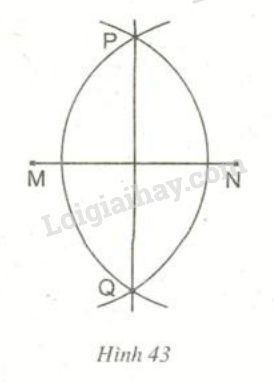
Chứng minh đường thẳng \(PQ\) được vẽ như hình \(43\) đúng là đường trung trực của đoạn thẳng MN.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Dựa vào cách vẽ.
- Áp dụng định lí 2 (định lí đảo): Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải chi tiết
Theo cách vẽ thì hai cung tròn tâm \(M\) và \(N\) có bán kính bằng nhau và cắt nhau tại \(P,Q\)
Do đó \(PM = PN\) và \(QM = QN\)
\( \Rightarrow P, Q\) cách đều hai mút \(M, N\) của đoạn thẳng \(MN.\)
Áp dụng định lí \(2\) suy ra \(P, Q\) nằm trên đường trung trực của đoạn thẳng \(MN\) hay đường thẳng \(PQ\) là đường trung trực của đoạn thẳng \(MN\) (điều phải chứng minh).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 46 trang 76 SGK Toán 7 tập 2
- Bài 47 trang 76 SGK Toán 7 tập 2
- Bài 48 trang 77 SGK Toán 7 tập 2
- Bài 49 trang 77 SGK Toán 7 tập 2
- Bài 50 trang 77 SGK Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
