Bài 14 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo

Hàm số (Sleft( r right) = frac{1}{{{r^4}}}) có thể được sử dụng để xác định sức cản (S)

Đề bài

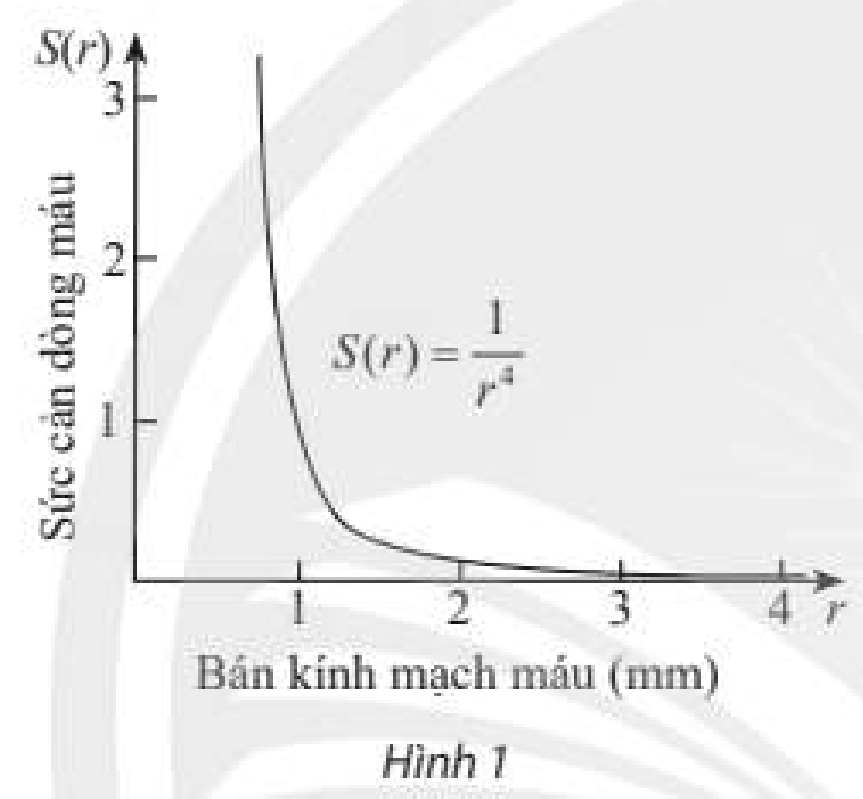
Hàm số \(S\left( r \right) = \frac{1}{{{r^4}}}\) có thể được sử dụng để xác định sức cản \(S\) của dòng máu trong mạch máu có bản kính \(r\) (tính theo milimét) (theo Bách khoa toàn thu Y học Harrison's internal medicine 21st edition”). Tìm tốc độ thay đổi của \(S\) theo \(r\) khi \(r = 0,8\).

Phương pháp giải - Xem chi tiết

Tính \(S'\left( {0,8} \right)\).

Lời giải chi tiết

Ta có:

\(s'\left( r \right) = {\left( {\frac{1}{{{r^4}}}} \right)^\prime } = {\left( {{r^{ - 4}}} \right)^\prime } = - 4.{r^{ - 5}} = - \frac{4}{{{r^5}}}\)

Tốc thay đổi của \(S\) theo \(r\) khi \(r = 0,8\) là: \(S'\left( {0,8} \right) = - \frac{4}{{0,{8^5}}} \approx - 12,21\).

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 7 phiếu

Bài tiếp theo

Bài 15 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo
Nhiệt độ cơ thể của một người trong thời gian bị bệnh được cho bởi công thức \(T\left( t \right) = - 0,1{t^2} + 1,2t + 98,6\)
Bài 16 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo
Hàm số (Rleft( v right) = frac{{6000}}{v}) có thể được sử dụng để xác định nhịp tim (R)
Bài 13 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo
Dân số \(P\) (tính theo nghìn người) của một thành phố nhỏ được cho bởi công thức \(P\left( t \right) = \frac{{500t}}{{{t^2} + 9}}\)
Bài 12 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Một vật chuyển động trên đường thẳng được xác định bởi công thức \(s\left( t \right) = 2{t^3} + 4t + 1\)
Bài 11 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Một viên soi rơi từ độ cao 44,1 m thì quãng đường rơi được biểu diễn bởi công thức \(s\left( t \right) = 4,9{t^2}\)
Bài 10 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tính đạo hàm cấp hai của các hàm số sau:
Bài 9 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tính đạo hàm của các hàm số sau:
Bài 8 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tính đạo hàm của các hàm số sau:
Bài 7 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tính đạo hàm của các hàm số sau:
Bài 6 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Cho hàm số \(f\left( x \right) = {x^2} - 2x + 3\) có đồ thị \(\left( C \right)\)
Bài 5 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Hàm số \(y = \frac{1}{{x + 1}}\) có đạo hàm cấp hai tại \(x = 1\) là
Bài 4 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Hàm số \(y = \frac{{x + 3}}{{x + 2}}\) có đạo hàm là
Bài 3 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Cho hai hàm số \(f\left( x \right) = 2{{\rm{x}}^3} - {x^2} + 3\) và \(g\left( x \right) = {x^3} + \frac{{{x^2}}}{2} - 5\).
Bài 1 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Cho hàm số (y = {x^3} - 3{{rm{x}}^2}). Tiếp tuyến với đồ thị của hàm số tại điểm (Mleft( { - 1;4} right)) có hệ số góc bằng
Bài 2 trang 51 SGK Toán 11 tập 2 - Chân trời sáng tạo
Hàm số \(y = - {x^2} + x + 7\) có đạo hàm tại \(x = 1\) bằng