Trắc nghiệm Bài 3: Phép cộng và phép trừ đa thức Toán 8 Kết nối tri thức
Đề bài
Cho đa thức \(P(x) = 3 + 5{{{x}}^2} - 3{{{x}}^3} + 4{{{x}}^2} - 2{{x}} - {x^3} + 5{{{x}}^5}.\)
Thu gọn và sắp xếp đa thức P(x) theo lũy thừa giảm dần của biến.
-
A.
\(P(x) = 3 + 2{{x}} + 9{{{x}}^2}\)
-
B.
\(P(x) = 5{{{x}}^5} - 4{{{x}}^3} + 9{{{x}}^2} - 2{{x}} + 3\)
-
C.
\(P(x) = 3{{{x}}^5} - 4{{{x}}^3} + 9{{{x}}^2}\)
-
D.
\(P(x) = 2{{x}} + 9\)
Thu gọn đa thức \(\left( { - 3{{{x}}^2}y - 2{{x}}{y^2} + 16} \right) + \left( { - 2{{{x}}^2}y + 5{{x}}{y^2} - 10} \right)\) ta được.
-
A.
\( - {x^2}y - 7{{x}}{y^2} + 26\)
-
B.
\( - 5{{{x}}^2}y + 3{{x}}{y^2} + 6\)
-
C.
\( - 5{{{x}}^2}y - 3{{x}}{y^2} + 6\)
-
D.
\(5{{{x}}^2}y - 3{{x}}{y^2} - 6\)
Hệ số cao nhất của đa thức: \(P(x) = 4{{{x}}^2}y + 6{{{x}}^3}{y^2} - 10{{{x}}^2}y + 4{{{x}}^3}{y^2}\)là
-
A.
10
-
B.
-6
-
C.
4
-
D.
3
Bậc của đa thức: \(2002{{{x}}^2}{y^3}z + 2{{{x}}^3}{y^2}{z^2} + 7{{{x}}^2}{y^3}z\) là:
-
A.
5
-
B.
6
-
C.
7
-
D.
8
Cho 2 đa thức:
\(\begin{array}{l}P(x) = {x^2} - 3{{x}} + 2\\Q(x) = {x^2} + x - 2\end{array}\)
Tính P(x) – Q(x):
-
A.
P(x) – Q(x) = -4x – 4
-
B.
P(x) – Q(x) = 4x – 4
-
C.
P(x) – Q(x) = -4x + 4
-
D.
P(x) – Q(x) = 4x + 4
Cho các đa thức:
\(\begin{array}{l}M = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 3\\N = {x^2}y - 2{{x}}y - 2\end{array}\)
Tính M + 2N
-
A.
\(3{{{x}}^3} - 1\)
-
B.
\(3{{{x}}^3} + {x^2}y - 2{{x}}y + 1\)
-
C.
\(3{{{x}}^3} - {x^2}y + 2{{x}}y - 1\)
-
D.
\(3{{{x}}^3} + {x^2}y - 2{{x}}y - 1\)
Cho các đa thức:
\(\begin{array}{l}M = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 2\\P = 3{{{x}}^3} - 2{{{x}}^2}y - xy + 3\end{array}\)
Tính M – P
-
A.
\({x^2}y + 3{{x}}y + 1\)
-
B.
\({x^2}y - 3{{x}}y - 1\)
-
C.
\( - {x^2}y + 3{{x}}y - 1\)
-
D.
\({x^2}y + 3{{x}}y - 1\)
-
A.
8
-
B.
9
-
C.
11
-
D.
10
Tính \(\left( {xy + {y^2} - {x^2}{y^2} - 2} \right) + \left( {{x^2}{y^2} + 5 - {y^2}} \right)\)
-
A.
xy + 3
-
B.
xy – 3
-
C.
–xy + 3
-
D.
–xy - 3
Cho các đa thức
\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C = - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)
Tính A + B +C:
-
A.
\(7{{{x}}^2} + 6{y^2}\)
-
B.
\(5{{{x}}^2} + 5{y^2}\)
-
C.
\(6{{{x}}^2} + 6{y^2}\)
-
D.
\(6{{{x}}^2} - 6{y^2}\)
Cho đa thức
\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C = - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)
Tính A – B – C:
-
A.
\( - 10{{{x}}^2} + 2{{x}}y\)
-
B.
\( - 2{{{x}}^2} - 10{{x}}y\)
-
C.
\(2{{{x}}^2} + 10{{x}}y\)
-
D.
\(2{{{x}}^2} - 10{{x}}y\)
Cho đa thức
\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C = - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)
Tính C – A – B:
-
A.
\(8{{{x}}^2} + 6{{x}}y + 2{y^2}\)
-
B.
\( - 8{{{x}}^2}{{ + 6x}}y - 2{y^2}\)
-
C.
\(8{{{x}}^2}{{ - 6x}}y - 2{y^2}\)
-
D.
\(8{{{x}}^2} - 6{{x}}y + 2{y^2}\)
Tìm đa thức M biết \(M + \left( {5{{{x}}^2} - 2{{x}}y} \right) = 6{{{x}}^2} + 10{{x}}y - {y^2}\)
-
A.
\(M = {x^2} + 12{{x}}y - {y^2}\)
-
B.
\(M = {x^2} - 12{{x}}y - {y^2}\)
-
C.
\(M = {x^2} + 12{{x}}y + {y^2}\)
-
D.
\(M = - {x^2} - 12{{x}}y - {y^2}\)
Tìm đa thức M biết: \(M - \left( {{{3x}}y - 4{y^2}} \right) = {{{x}}^2}{{ - 7x}}y + 8{y^2}\)
-
A.
\(M = {x^2}{{ - 4x}}y + 4{y^2}\)
-
B.
\(M = {x^2}{{ + 4x}}y + 4{y^2}\)
-
C.
\(M = - {x^2}{{ - 4x}}y + 4{y^2}\)
-
D.
\(M = {x^2} + 10{{x}}y + 4{y^2}\)
Tính giá trị của đa thức
\(C = xy + {x^2}{y^2} + {x^3}{y^3} + ...... + {x^{100}}{y^{100}}\) tại x = -1; y = -1
-
A.
-100
-
B.
100
-
C.
0
-
D.
50
Tính giá trị của đa thức
\(N = {x^3} + {x^2}y - 2{{{x}}^2} - xy - {y^2} + 3y + x - 1\) biết x + y – 2 = 0
-
A.
-1
-
B.
0
-
C.
2
-
D.
1
Cho
\(\begin{array}{l}M = x - (y - z) - 2{{x}} + y + z - (2 - x - y)\\N = x - \left[ {x - \left( {y - 2{{z}}} \right) - 2{{z}}} \right]\end{array}\)
Tính M – N
-
A.
-2z + 2
-
B.
-2x – 2y – 2
-
C.
2z – 2
-
D.
-2x + 2y - 2
Nếu 3(4x + 5y) = P thì 12(12x+15y) bằng
-
A.
12P
-
B.
36P
-
C.
4P
-
D.
20P
Bác Nam có một mảnh vườn hình chữ nhật có chiều dài là: \(2{y^2} + 12 + xy(m)\); chiều rộng là 2xy.(m). tính chu vi của khu vườn biết x = 4 và y = 4.
-
A.
184 m
-
B.
60m
-
C.
32m
-
D.
184\({m^2}\)
Khu vườn trồng mía của nhà bác Minh ban đầu có dạng hình vuông biết chu vi hình vuông là 20(m) sau đó mở rộng bên phải thêm y(m) phía dưới thêm 8x(m) nên mảnh vườn trở thành hình chữ nhật. Tính chu vi của khu vườn sau khi được mở rộng theo x, y
-
A.
y +5
-
B.
8x + 5
-
C.
2y +16x + 20
-
D.
4x + 8y
Một cửa hàng buổi sáng bán được: \(8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 3{{{x}}^5}{y^4}\); buổi chiều bán được: \({x^6}{y^5} - {x^5}{y^4}\)(bao gạo). Tính số bao gạo mà của hàng bán được trong một ngày.
-
A.
\(8{{{x}}^3}y + 6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
-
B.
\(8{{{x}}^3}y + 6{{{x}}^6}{y^5}\)
-
C.
\(8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
-
D.
\(6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
Cho \(P = xyz + {x^2}{y^2}{z^2} + .... + {x^{2022}}{y^{2022}}{z^{2022}}\). Tính P biết: x = y = 1; z = -1.
-
A.
P = -2022
-
B.
P = 0
-
C.
P = 2022
-
D.
P = 1011
Cho đa thức A = 3x – 1; B = 2y + 4x. Tính đa thức C = A + B khi x = 2y = 1.
-
A.
C = 8
-
B.
C = 7
-
C.
C = 9
-
D.
C = 10
Cho
\(\begin{array}{l}f\left( x \right) = {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1\\g\left( x \right) = - {x^{2n + 1}} + {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1\end{array}\)
Biết \(h\left( x \right) = f\left( x \right) - g\left( x \right)\). Tính \(h\left( {\frac{1}{{10}}} \right)\)
-
A.
\(h\left( {\frac{1}{{10}}} \right) = \frac{{ - 1}}{{{{10}^{2n + 1}}}}\)
-
B.
\(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n + 1}}}}\)
-
C.
\(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n - 1}}}}\)
-
D.
\(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n - 1}}}}\)
Một tấm bìa cứng hình chữ nhật có chiều dài là x + 43 (cm), chiều rộng x+30 (cm). Người ta cắt ở mỗi góc của tấm bìa hình vuông cạnh \({y^2} + 1\) và xếp phần còn lại thành một cái hộp không nắp.
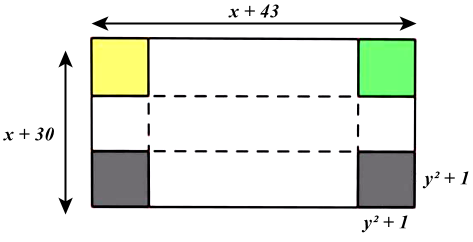
Tính chiều dài của hình hộp chữ nhật.
-
A.
\(x + 2{y^2} + 41(cm)\)
-
B.
\({x^2} + 2{y^2}\left( {cm} \right)\)
-
C.
\(x - 2{y^2} + 41\left( {cm} \right)\)
-
D.
\(x - 2{y^2}\left( {cm} \right)\)
Tính chiều rộng của hình hộp chữ nhật.
-
A.
\({x^2} - 2{y^2}(cm)\)
-
B.
\(x - 2{y^2} + 28\left( {cm} \right)\)
-
C.
\(x - {y^2}\left( {cm} \right)\)
-
D.
\(x + 28\left( {cm} \right)\)
Lời giải và đáp án
Cho đa thức \(P(x) = 3 + 5{{{x}}^2} - 3{{{x}}^3} + 4{{{x}}^2} - 2{{x}} - {x^3} + 5{{{x}}^5}.\)
Thu gọn và sắp xếp đa thức P(x) theo lũy thừa giảm dần của biến.
-
A.
\(P(x) = 3 + 2{{x}} + 9{{{x}}^2}\)
-
B.
\(P(x) = 5{{{x}}^5} - 4{{{x}}^3} + 9{{{x}}^2} - 2{{x}} + 3\)
-
C.
\(P(x) = 3{{{x}}^5} - 4{{{x}}^3} + 9{{{x}}^2}\)
-
D.
\(P(x) = 2{{x}} + 9\)
Đáp án : B
\(\begin{array}{l}P(x) = 3 + 5{{{x}}^2} - 3{{{x}}^3} + 4{{{x}}^2} - 2{{x}} - {x^3} + 5{{{x}}^5}\\P(x) = 5{{{x}}^5} + ( - 3{{{x}}^3} - {x^3}) + (5{{{x}}^2} + 4{{{x}}^2}) - 2{{x}} + 3\\P(x) = 5{{{x}}^5} - 4{{{x}}^3} + 9{{{x}}^2} - 2{{x}} + 3\end{array}\)
Thu gọn đa thức \(\left( { - 3{{{x}}^2}y - 2{{x}}{y^2} + 16} \right) + \left( { - 2{{{x}}^2}y + 5{{x}}{y^2} - 10} \right)\) ta được.
-
A.
\( - {x^2}y - 7{{x}}{y^2} + 26\)
-
B.
\( - 5{{{x}}^2}y + 3{{x}}{y^2} + 6\)
-
C.
\( - 5{{{x}}^2}y - 3{{x}}{y^2} + 6\)
-
D.
\(5{{{x}}^2}y - 3{{x}}{y^2} - 6\)
Đáp án : B
\(\begin{array}{l}\left( { - 3{{{x}}^2}y - 2{{x}}{y^2} + 16} \right) + \left( { - 2{{{x}}^2}y + 5{{x}}{y^2} - 10} \right)\\ = - 3{{{x}}^2}y - 2{{x}}{y^2} + 16 - 2{{{x}}^2}y + 5{{x}}{y^2} - 10\\ = \left( { - 3{{{x}}^2}y - 2{{{x}}^2}y} \right) + \left( { - 2{{x}}{y^2} + 5{{x}}{y^2}} \right) + \left( {16 - 10} \right)\\ = - 5{{{x}}^2}y + 3{{x}}{y^2} + 6\end{array}\)
Hệ số cao nhất của đa thức: \(P(x) = 4{{{x}}^2}y + 6{{{x}}^3}{y^2} - 10{{{x}}^2}y + 4{{{x}}^3}{y^2}\)là
-
A.
10
-
B.
-6
-
C.
4
-
D.
3
Đáp án : A
Ta có:
\(\begin{array}{l}P(x) = 4{{{x}}^2}y + 6{{{x}}^3}{y^2} - 10{{{x}}^2}y + 4{{{x}}^3}{y^2}\\ = \left( {4{{{x}}^2}y - 10{{{x}}^2}{{y}}} \right) + \left( {6{{{x}}^3}{y^2} + 4{{{x}}^3}{y^2}} \right)\\ = - 6{{{x}}^2}y + 10{{{x}}^3}{y^2}\end{array}\)
Suy ra hệ số cao nhất của P(x) là hệ số của \({{{x}}^3}{y^2}\) nên hệ số cao nhất của P(x) là 10
Bậc của đa thức: \(2002{{{x}}^2}{y^3}z + 2{{{x}}^3}{y^2}{z^2} + 7{{{x}}^2}{y^3}z\) là:
-
A.
5
-
B.
6
-
C.
7
-
D.
8
Đáp án : C
\(\begin{array}{l}2002{{{x}}^2}{y^3}z + 2{{{x}}^3}{y^2}{z^2} + 7{{{x}}^2}{y^3}z\\ = \left( {2002{{{x}}^2}{y^3}z + 7{{{x}}^2}{y^3}z} \right) + 2{{{x}}^3}{y^2}{z^2}\\ = 2009{{{x}}^2}{y^3}z + 2{{{x}}^3}{y^2}{z^2}\end{array}\)
Bậc của đa thức P(x) là: 7.
Cho 2 đa thức:
\(\begin{array}{l}P(x) = {x^2} - 3{{x}} + 2\\Q(x) = {x^2} + x - 2\end{array}\)
Tính P(x) – Q(x):
-
A.
P(x) – Q(x) = -4x – 4
-
B.
P(x) – Q(x) = 4x – 4
-
C.
P(x) – Q(x) = -4x + 4
-
D.
P(x) – Q(x) = 4x + 4
Đáp án : C
\(\begin{array}{l}P(x) - Q(x)\\ = ({x^2} - 3{{x}} + 2) - ({x^2} + x - 2)\\ = {x^2} - 3{{x}} + 2 - {x^2} - x + 2\\ = - 4{{x}} + 4\end{array}\)
Cho các đa thức:
\(\begin{array}{l}M = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 3\\N = {x^2}y - 2{{x}}y - 2\end{array}\)
Tính M + 2N
-
A.
\(3{{{x}}^3} - 1\)
-
B.
\(3{{{x}}^3} + {x^2}y - 2{{x}}y + 1\)
-
C.
\(3{{{x}}^3} - {x^2}y + 2{{x}}y - 1\)
-
D.
\(3{{{x}}^3} + {x^2}y - 2{{x}}y - 1\)
Đáp án : D
\(\begin{array}{l}M + 2N\\ = \left( {3{{{x}}^3} - {x^2}y + 2{{x}}y + 3} \right) + 2({x^2}y - 2{{x}}y - 2)\\ = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 3 + 2{{{x}}^2}y - 4{{x}}y - 4\\ = 3{{{x}}^3} + {x^2}y - 2{{x}}y - 1\end{array}\)
Đáp án đúng là : D
Cho các đa thức:
\(\begin{array}{l}M = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 2\\P = 3{{{x}}^3} - 2{{{x}}^2}y - xy + 3\end{array}\)
Tính M – P
-
A.
\({x^2}y + 3{{x}}y + 1\)
-
B.
\({x^2}y - 3{{x}}y - 1\)
-
C.
\( - {x^2}y + 3{{x}}y - 1\)
-
D.
\({x^2}y + 3{{x}}y - 1\)
Đáp án : D
Tính M – P và nhóm các đơn thức đồng dạng.
\(\begin{array}{l}M - P\\ = \left( {3{{{x}}^3} - {x^2}y + 2{{x}}y + 2} \right) - \left( {3{{{x}}^3} - 2{{{x}}^2}y - xy + 3} \right)\\ = 3{{{x}}^3} - {x^2}y + 2{{x}}y + 2 - 3{{{x}}^3} + 2{{{x}}^2}y + xy - 3\\ = {x^2}y + 3{{x}}y - 1\end{array}\)
-
A.
8
-
B.
9
-
C.
11
-
D.
10
Đáp án : C
Thu gọn đa thức theo quy tắc cộng trừ đa thức
Thay x = -1 vào đa thức f(x) thu gọn
Ta có: \(\begin{array}{l}f(x) = 3{{{x}}^4} + 2{{{x}}^3} - 2{{{x}}^4} + {x^2} - 5{{x}} + 6\\ = (3{x^4} - 2{{x}}{}^4) + 2{{{x}}^3} + {x^2} - 5{{x}} + 6\\ = {x^4} + 2{{{x}}^3} + {x^2} - 5{{x}} + 6\end{array}\)
Sau đó thay x = -1 vào đa thức \(f\left( x \right)\)thu gọn ta được
\(f\left( { - 1} \right) = {\left( { - 1} \right)^4} + 2{\left( { - 1} \right)^3} + {\left( { - 1} \right)^2} - 5\left( { - 1} \right) + 6 = 11\)
Tính \(\left( {xy + {y^2} - {x^2}{y^2} - 2} \right) + \left( {{x^2}{y^2} + 5 - {y^2}} \right)\)
-
A.
xy + 3
-
B.
xy – 3
-
C.
–xy + 3
-
D.
–xy - 3
Đáp án : A
\(\begin{array}{l}\left( {xy + {y^2} - {x^2}{y^2} - 2} \right) + \left( {{x^2}{y^2} + 5 - {y^2}} \right)\\ = xy + {y^2} - {x^2}{y^2} - 2 + {x^2}{y^2} + 5 - {y^2}\\ = \left( { - {x^2}{y^2} + {x^2}{y^2}} \right) + xy + \left( {{y^2} - {y^2}} \right) + \left( { - 2 + 5} \right)\\ = xy + 3\end{array}\)
Cho các đa thức
\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C = - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)
Tính A + B +C:
-
A.
\(7{{{x}}^2} + 6{y^2}\)
-
B.
\(5{{{x}}^2} + 5{y^2}\)
-
C.
\(6{{{x}}^2} + 6{y^2}\)
-
D.
\(6{{{x}}^2} - 6{y^2}\)
Đáp án : C
\(\begin{array}{l}A + B + C = (4{{{x}}^2} - 5{{x}}y + 3{y^2}) + (3{{{x}}^2} + 2{{x}}y + {y^2}) + ( - {x^2} + 3{{x}}y + 2{y^2})\\ = 4{{{x}}^2} - 5{{x}}y + 3{y^2} + 3{{{x}}^2} + 2{{x}}y + {y^2} - {x^2} + 3{{x}}y + 2{y^2}\\ = \left( {4{{{x}}^2} + 3{{{x}}^2} - {x^2}} \right) + \left( { - 5{{x}}y + 2{{x}}y + 3{{x}}y} \right) + \left( {3{y^2} + {y^2} + 2{y^2}} \right)\\ = 6{{{x}}^2} + 6{y^2}\end{array}\)
Cho đa thức
\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C = - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)
Tính A – B – C:
-
A.
\( - 10{{{x}}^2} + 2{{x}}y\)
-
B.
\( - 2{{{x}}^2} - 10{{x}}y\)
-
C.
\(2{{{x}}^2} + 10{{x}}y\)
-
D.
\(2{{{x}}^2} - 10{{x}}y\)
Đáp án : D
\(\begin{array}{l}A - B - C = \left( {4{{{x}}^2} - 5{{x}}y + 3{y^2}} \right) - \left( {3{{{x}}^2} + 2{{x}}y + {y^2}} \right) - \left( { - {x^2} + 3{{x}}y + 2{y^2}} \right)\\ = 4{{{x}}^2} - 5{{x}}y + 3{y^2} - 3{{{x}}^2} - 2{{x}}y - {y^2} + {x^2} - 3{{x}}y - 2{y^2}\\ = \left( {4{{{x}}^2} - 3{{{x}}^2} + {x^2}} \right) + \left( { - 5{{x}}y - 2{{x}}y - 3{{x}}y} \right) + \left( {3{y^2} - {y^2} - 2{y^2}} \right)\\ = 2{{{x}}^2} - 10{{x}}y\end{array}\)
Cho đa thức
\(\begin{array}{l}A = 4{{{x}}^2} - 5{{x}}y + 3{y^2}\\B = 3{{{x}}^2} + 2{{x}}y + {y^2}\\C = - {x^2} + 3{{x}}y + 2{y^2}\end{array}\)
Tính C – A – B:
-
A.
\(8{{{x}}^2} + 6{{x}}y + 2{y^2}\)
-
B.
\( - 8{{{x}}^2}{{ + 6x}}y - 2{y^2}\)
-
C.
\(8{{{x}}^2}{{ - 6x}}y - 2{y^2}\)
-
D.
\(8{{{x}}^2} - 6{{x}}y + 2{y^2}\)
Đáp án : B
\(\begin{array}{l}C - A - B = \left( { - {x^2} + 3{{x}}y + 2{y^2}} \right) - \left( {4{{{x}}^2} - 5{{x}}y + 3{y^2}} \right) - \left( {3{{{x}}^2} + 2{{x}}y + {y^2}} \right) \\ = - {x^2} + 3{{x}}y + 2{y^2} - 4{{{x}}^2} + 5{{x}}y - 3{y^2} - 3{{{x}}^2} - 2{{x}}y - {y^2} \\ = \left( { - 4{{{x}}^2} - 3{{{x}}^2} - {x^2}} \right) + \left( {5{{x}}y - 2{{x}}y + 3{{x}}y} \right) + \left( { - 3{y^2} - {y^2} + 2{y^2}} \right)\\ = - 8{{{x}}^2}{{ + 6x}}y - 2{y^2}\end{array}\)
Tìm đa thức M biết \(M + \left( {5{{{x}}^2} - 2{{x}}y} \right) = 6{{{x}}^2} + 10{{x}}y - {y^2}\)
-
A.
\(M = {x^2} + 12{{x}}y - {y^2}\)
-
B.
\(M = {x^2} - 12{{x}}y - {y^2}\)
-
C.
\(M = {x^2} + 12{{x}}y + {y^2}\)
-
D.
\(M = - {x^2} - 12{{x}}y - {y^2}\)
Đáp án : A
Áp dụng: \(M + A = B \) thì \(M = B - A\)
Ta có:
\(M + \left( {5{{{x}}^2} - 2{{x}}y} \right) = 6{{{x}}^2} + 10{{x}}y - {y^2}\)
suy ra \(M = 6{{{x}}^2} + 10{{x}}y - {y^2} - \left( {5{{{x}}^2} - 2{{xy}}} \right)\)
\(M = 6{{{x}}^2} + 10{{x}}y - {y^2} - {5{{{x}}^2} + 2{{xy}}}\)
\(M = \left( {6{{{x}}^2} - 5{{{x}}^2}} \right) + \left( {10{{x}}y + 2{{x}}y} \right) - {y^2}\)
\(M = {x^2} + 12{{x}}y - {y^2}\)
Tìm đa thức M biết: \(M - \left( {{{3x}}y - 4{y^2}} \right) = {{{x}}^2}{{ - 7x}}y + 8{y^2}\)
-
A.
\(M = {x^2}{{ - 4x}}y + 4{y^2}\)
-
B.
\(M = {x^2}{{ + 4x}}y + 4{y^2}\)
-
C.
\(M = - {x^2}{{ - 4x}}y + 4{y^2}\)
-
D.
\(M = {x^2} + 10{{x}}y + 4{y^2}\)
Đáp án : A
\(\begin{array}{l}M - \left( {{{3x}}y - 4{y^2}} \right) = {{{x}}^2}{{ - 7x}}y + 8{y^2}\\ \Rightarrow M = {x^2} - 7{{x}}y + 8{y^2} + \left( {3{{x}}y - 4{y^2}} \right)\\M = {x^2} + \left( { - 7{{x}}y + 3{{x}}y} \right) + \left( {8{y^2} - 4{y^2}} \right)\\ \Rightarrow M = {x^2} - 4{{x}}y + 4{y^2}\end{array}\)
Tính giá trị của đa thức
\(C = xy + {x^2}{y^2} + {x^3}{y^3} + ...... + {x^{100}}{y^{100}}\) tại x = -1; y = -1
-
A.
-100
-
B.
100
-
C.
0
-
D.
50
Đáp án : B
\(\begin{array}{l}C = ( - 1)\left( { - 1} \right) + {\left( { - 1} \right)^2}{\left( { - 1} \right)^2} + {\left( { - 1} \right)^3}{\left( { - 1} \right)^3} + ........... + {\left( { - 1} \right)^{100}}{\left( { - 1} \right)^{100}}\\C = 1 + 1 + 1 + ..... + 1 = 100\end{array}\)
Tính giá trị của đa thức
\(N = {x^3} + {x^2}y - 2{{{x}}^2} - xy - {y^2} + 3y + x - 1\) biết x + y – 2 = 0
-
A.
-1
-
B.
0
-
C.
2
-
D.
1
Đáp án : D
\(\begin{array}{l}N = {x^3} + {x^2}y - 2{{{x}}^2} - xy - {y^2} + 3y + x - 1\\ = \left( {{x^3} + {x^2}y - 2{{{x}}^2}} \right) + \left( { - xy - {y^2} + 2y} \right) + y + x - 1\\ = {x^2}\left( {x + y - 2} \right) - y\left( {x + y - 2} \right) + \left( {x + y - 2} \right) + 1\\ = {x^2}.0 - y.0 + 0 + 1 = 1\end{array}\)
Cho
\(\begin{array}{l}M = x - (y - z) - 2{{x}} + y + z - (2 - x - y)\\N = x - \left[ {x - \left( {y - 2{{z}}} \right) - 2{{z}}} \right]\end{array}\)
Tính M – N
-
A.
-2z + 2
-
B.
-2x – 2y – 2
-
C.
2z – 2
-
D.
-2x + 2y - 2
Đáp án : C
Ta có:
\(\begin{array}{l}M = x - \left( {y - z} \right) - 2{{x}} + y + z - \left( {2 - x - y} \right)\\ = x - y + z - 2{{x}} + y + z - 2 + x + y\\ = y + 2{{z}} - 2\\N = x - \left[ {x - \left( {y - 2{{z}}} \right) - 2{{z}}} \right]\\ = x - \left( {x - y + 2{{z}} - 2{{z}}} \right) = x - x + y = y\\ \text{suy ra } M - N = y + 2{{z}} - 2 - y = 2{{z}} - 2\end{array}\)
Nếu 3(4x + 5y) = P thì 12(12x+15y) bằng
-
A.
12P
-
B.
36P
-
C.
4P
-
D.
20P
Đáp án : A
12(12x +15y) = 12(3.4x + 3.5y) = 12.3(4x +5y) = 12P
Bác Nam có một mảnh vườn hình chữ nhật có chiều dài là: \(2{y^2} + 12 + xy(m)\); chiều rộng là 2xy.(m). tính chu vi của khu vườn biết x = 4 và y = 4.
-
A.
184 m
-
B.
60m
-
C.
32m
-
D.
184\({m^2}\)
Đáp án : A
\(2.\left( {2{y^2} + 12 + xy + 2{{x}}y} \right) = 2.\left( {2{y^2} + 12 + 3{{x}}y} \right) = 4{y^2} + 24 + 6{{x}}y\)
Thay x = 4; y = 4 vào công thức chu vi ta được:
\({4.4^2} + 24 + 6.4.4 = 184m\)
Khu vườn trồng mía của nhà bác Minh ban đầu có dạng hình vuông biết chu vi hình vuông là 20(m) sau đó mở rộng bên phải thêm y(m) phía dưới thêm 8x(m) nên mảnh vườn trở thành hình chữ nhật. Tính chu vi của khu vườn sau khi được mở rộng theo x, y
-
A.
y +5
-
B.
8x + 5
-
C.
2y +16x + 20
-
D.
4x + 8y
Đáp án : C
Xác định chiều dài, chiều rộng của khu vườn sau khi được mở rộng. Tính chu vi của khu vườn sau khi mở rộng
Chiều rộng của khu vườn sau khi được mở rộng là: y +5 (m)
Chiều dài của khu vườn sau khi được mở rộng là: 8x + 5 (m)
Chu vi của khu vườn là: 2(y + 5 + 8x + 5) = 2.(y + 8x + 10) = 2y + 16x + 20 (m)
Một cửa hàng buổi sáng bán được: \(8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 3{{{x}}^5}{y^4}\); buổi chiều bán được: \({x^6}{y^5} - {x^5}{y^4}\)(bao gạo). Tính số bao gạo mà của hàng bán được trong một ngày.
-
A.
\(8{{{x}}^3}y + 6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
-
B.
\(8{{{x}}^3}y + 6{{{x}}^6}{y^5}\)
-
C.
\(8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
-
D.
\(6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\)
Đáp án : A
Cộng số bao gạo bán được của buổi sáng và buổi chiều rồi rút gọn.
\(\begin{array}{l}\left( {8{{{x}}^3}y + 5{{{x}}^6}{y^5} - 3{{{x}}^5}{y^4}} \right) + \left( {{x^6}{y^5} - {x^5}{y^4}} \right)\\ = 8{{{x}}^3}y + 6{{{x}}^6}{y^5} - 4{{{x}}^5}{y^4}\end{array}\)
Cho \(P = xyz + {x^2}{y^2}{z^2} + .... + {x^{2022}}{y^{2022}}{z^{2022}}\). Tính P biết: x = y = 1; z = -1.
-
A.
P = -2022
-
B.
P = 0
-
C.
P = 2022
-
D.
P = 1011
Đáp án : B
\(\begin{array}{l}P = 1.1\left( { - 1} \right) + {1^2}{.1^2}{\left( { - 1} \right)^2} + .... + {1^{2022}}{.1^{2022}}{\left( { - 1} \right)^{2022}}\\ = \left( { - 1} \right) + 1 + \left( { - 1} \right) + .... + \left( { - 1} \right) = 0\end{array}\)
Cho đa thức A = 3x – 1; B = 2y + 4x. Tính đa thức C = A + B khi x = 2y = 1.
-
A.
C = 8
-
B.
C = 7
-
C.
C = 9
-
D.
C = 10
Đáp án : B
Ta có: C = A + B = 3x – 1 +2y +4x = 7x + 2y - 1 với
\(x = 2y = 1 \Rightarrow \left\{ \begin{array}{l}x = 1\\2y = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 1\\y = \frac{1}{2}\end{array} \right.\) Thay \(x = 1;y = \frac{1}{2}\)vào C ta được:
\(C = 7.1 + 2.\frac{1}{2} - 1 = 7 + 1 - 1 = 7\)
Cho
\(\begin{array}{l}f\left( x \right) = {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1\\g\left( x \right) = - {x^{2n + 1}} + {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1\end{array}\)
Biết \(h\left( x \right) = f\left( x \right) - g\left( x \right)\). Tính \(h\left( {\frac{1}{{10}}} \right)\)
-
A.
\(h\left( {\frac{1}{{10}}} \right) = \frac{{ - 1}}{{{{10}^{2n + 1}}}}\)
-
B.
\(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n + 1}}}}\)
-
C.
\(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n - 1}}}}\)
-
D.
\(h\left( {\frac{1}{{10}}} \right) = \frac{1}{{{{10}^{2n - 1}}}}\)
Đáp án : B
Thay \(x = \frac{1}{{10}}\)vào h(x)
\(\begin{array}{l}h\left( x \right) = f\left( x \right) - g\left( x \right)\\ = \left( {{x^{2n}} - {x^{2n - 1}} + ..... + {x^2} - x + 1} \right) - \left( { - {x^{2n + 1}} + {x^{2n}} - {x^{2n - 1}} + .... + {x^2} - x + 1} \right)\\ = {x^{2n}} - {x^{2n - 1}} + ..... + {x^2} - x + 1 + {x^{2n + 1}} - {x^{2n}} + {x^{2n + 1}} - .... - {x^2} + x - 1\\ = {x^{2n + 1}} + \left( {{x^{2n}} - {x^{2n}}} \right) + \left( { - {x^{2n - 1}} + {x^{2n - 1}}} \right) + .... + \left( {{x^2} - {x^2}} \right) + \left( { - x + x} \right) + \left( {1 - 1} \right)\\ = {x^{2n + 1}}\end{array}\)
Thay \(x = \frac{1}{{10}}\)vào h(x) ta được:
\(h\left( {\frac{1}{{10}}} \right) = {\left( {\frac{1}{{10}}} \right)^{2n + 1}} = \frac{1}{{{{10}^{2n + 1}}}}\)
Một tấm bìa cứng hình chữ nhật có chiều dài là x + 43 (cm), chiều rộng x+30 (cm). Người ta cắt ở mỗi góc của tấm bìa hình vuông cạnh \({y^2} + 1\) và xếp phần còn lại thành một cái hộp không nắp.

Tính chiều dài của hình hộp chữ nhật.
-
A.
\(x + 2{y^2} + 41(cm)\)
-
B.
\({x^2} + 2{y^2}\left( {cm} \right)\)
-
C.
\(x - 2{y^2} + 41\left( {cm} \right)\)
-
D.
\(x - 2{y^2}\left( {cm} \right)\)
Đáp án: C
Chiều dài của hình hộp chữ nhật bằng chiều dài ban đầu trừ đi hai lần cạnh của hình vuông
Chiều dài của hình hộp chữ nhật là:
\(\left( {x + 43} \right) - \left( {{y^2} + 1} \right).2 = x - 2{y^2} + 41(cm)\)
Tính chiều rộng của hình hộp chữ nhật.
-
A.
\({x^2} - 2{y^2}(cm)\)
-
B.
\(x - 2{y^2} + 28\left( {cm} \right)\)
-
C.
\(x - {y^2}\left( {cm} \right)\)
-
D.
\(x + 28\left( {cm} \right)\)
Đáp án: B
Chiều rộng của hình hộp chữ nhật bằng chiều rộng ban đầu trừ đi hai lần cạnh của hình vuông.
Chiều rộng của hình hộp chữ nhật là:
\(\left( {x + 30} \right) - \left( {{y^2} + 1} \right).2 = x - 2{y^2} + 28(cm)\)
Luyện tập và củng cố kiến thức Bài 4: Phép nhân đa thức Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Phép chia đa thức cho đơn thức Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Đa thức Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Đơn thức Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 39: Hình chóp tứ giác đều Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 38: Hình chóp tam giác đều Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 37: Hình đồng dạng Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 36: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Kết nối tri thức
- Trắc nghiệm Bài 35: Định lí Pythagore và ứng dụng Toán 8 Kết nối tri thức










Danh sách bình luận